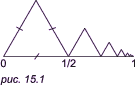
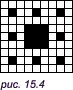Часть III / Лекция 15. Построение реалистических изображений методами фрактальной геометрии

Необычные функции

Фракталы с большой точностью могут описывать многие физические явления и природные образования: горы, облака, деревья, ландшафты... Впервые фрактальную природу нашего мира подметил Бенуа Мандельброт. Слово «фрактал» происходит от латинского fractus, что означает «дробный», и frahgere — «ломать». Главной особенностью фракталов является их бесконечное самоподобие.

Фрактальные функции широко используются в качестве инструментов для реалистичного построения природных объектов, бесконечно сложных узоров и картин... В машинной графике метод построения фрактальных поверхностей первыми применили Карпентер, Фурнье и Фассел. Итак, фракталы — это функции, которые ведут себя не совсем обычно и могут не подчиняться основным законам поведения «обычных» функций.

Фрактальная поверхность состоит из случайно заданных полигональных или биполиноминальных поверхностей. Одно из преимуществ таких поверхностей в том, что можно получить любой уровень их детализации, независимо от того, насколько близко мы к ним находимся. В машинной графике фракталы строятся простыми и быстрыми итерационными алгоритмами.

Попробуем изобразить линию-фрактал, имеющую бесконечное число максимумов и минимумов на отрезке (0, 1). Такая линия показана на рис. 15.1, ей соответствует следующая функция:

f(x) =		x * cos(p/x), x <> 0
		0, x = 0

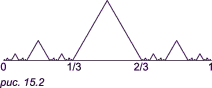
Построить эту функцию можно так: разбиваем отрезок на 1/2, строим равносторонний треугольник; одну из сторон делим на 2 и от него строим следующий треугольник с меньшей стороной и так до бесконечности...

Если делить отрезок не на две, а на три части, то можно построить другую линию (см. рис. 15.2).

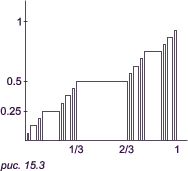
Такие функции обладают интересными и необычными свойствами. Например, фрактал, показанный на рис. 15.2, имеет такие свойства: число треугольников («крыш») бесконечно; на такой линии расположено бесконечное число точек, которые не защищены «крышей» — это точки 0, ..., 1/9, 2/9, ..., 1/3, 2/3, ..., 1.

Чертова лестница

Рассмотрим еще некоторые виды фракталов. На рис. 15.3 изображена лестница с бесконечным числом ступеней.

Вычислим общую длину такой лестницы: 1 * 1/3 — первая ступень, 2 * 1/9 — вторые ступени, 4 * 1/27 — третьи ступени и т. д. Общая длина ступеней равна единице: 1 * 1/3 + 2 * 1/9 + 4 * 1/27 + ... = 1. Но при этом существует бесконечно много точек, которые не принадлежат ступеням, это так называемые «мокрые» точки: 0, ..., 1/9, 2/9, ..., 1/3, 2/3, ..., 1. (Они называются «мокрыми», потому что если начать лить на ступени воду, то она свободно просочится между стенками ступеней и попадет как раз в «мокрые» точки.)

Этим простым примером иллюстрируется важнейшее положение современной математики о том, что часть равна целому. Мы только что показали, что между ступенями имеется бесчисленное число «мокрых» точек, образующих разрывы. Но, тем не менее, сумма длин всех ступеней строго равна единице! То есть «часть», составленная из длин всех ступеней, равна «целому», представляющему собой отрезок единичной длины!

Ковер Серпинского

Будем разбивать квадрат на 9 частей и каждый раз выкидывать среднюю. Таким образом мы получаем абсолютно дырявое тело — линию, где нет целых частей:

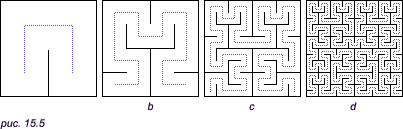
Линия Пеано

Линия Пеано — это непрерывная линия, проходящая через все точки квадрата. Когда число замен линий на скобки будет стремиться к бесконечности в квадрате на рис. 15.5 не останется пустых мест:

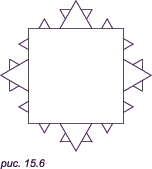
Фрактал Коши

«Бесконечно колючая линия» (рис. 15.6), периметр P которой вычисляется по формуле: P = 3 * (4/3)ⁿ, где n — номер итерации (на рисунке показана линия для n = 3).

Если n бесконечно, то длина линии бесконечна. Примечательно то, что в конечном куске плоскости можно уместить бесконечно длинную линию.

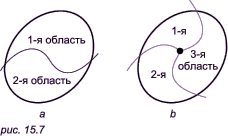
Линия Бауэра

Как известно, границей двух областей на плоскости является линия (рис. 15.7a), границей трех областей — точка рис. 15.7b.

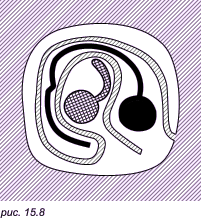
Кажется очевидным, что линия не может быть совместной границей более чем двух областей на плоскости, которые примыкают к этой линии на всем ее протяжении. Однако здесь интуиция нас обманывает, и мы можем увидеть линию, которая является границей трех областей: к любой точке острова можно провести три канала, которые не будут пересекаться (рис. 15.8). Подробнее см. здесь.