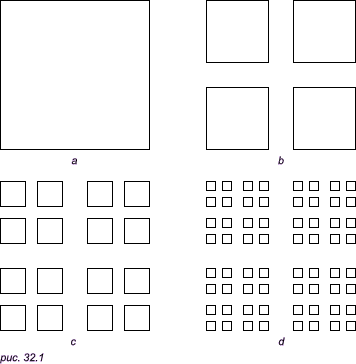
Что такое линия. Кривая Пеано

Евклид определяет линию как «длину ширины». Это, конечно, не определение, а лишь наглядное описание линий. Следующий пример показывает, однако, что это описание вряд ли можно считать удачным.

Пример 1. Возьмем квадрат единичной площади (рис. 32.1а) и выбросим из него крест (рис. 32.1b), причем ширину полосок креста подберем так, чтобы его площадь была равна 1/4. В каждом из оставшихся квадратов снова вырежем по кресту (рис. 32.1c), причем так, чтобы сумма площадей крестов была равна 1/8. В каждом из оставшихся 16 маленьких квадратов вновь выбросим по кресту (рис. 32.1d) так, чтобы сумма площадей выбрасываемых кусков была равна 1/16, и так далее.

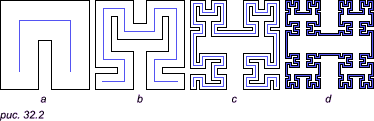
Обозначим через A «предельную фигуру», то есть пересечение фигур A₁, A₂, ..., A_n, где A_n — фигура, которая остается после проведения n этапов построения.

Фигура A как бы «расcыпается» на отдельные точки (ибо остающиеся квадратики с каждым разом делаются все меньше) и тем не менее имеет положительную площадь. В самом деле, сначала мы выбросили из квадрата 1/4 его площади, затем 1/8, затем 1/16 и так далее. В пределе у нас останется фигура A, имеющая площадь 1 - (1/4 + 1/8 + 1/16 + ...). Так как сумма бесконечно убывающей геометрической прогрессии, записанной в скобках, равна 1/2, то площадь предельной фигуры A равна 1/2.

Построим далее простую дугу (то есть фигуру, гомоморфную отрезку), которая проходит через все точки множества A. Для этого возьмем изогнутую полоску, содержащую четыре квадрата (рис. 32.2а), полученных на первом этапе построения. Затем сделаем полоску более узкой и изогнутой, так что она будет содержать все квадраты, полученные на втором этапе (рис. 32.2b), затем на третьем (рис. 32.2c) и так далее.

После n этапов этого построения мы получаем полоcку B_n, которая содержится в предыдущих полосках и содержит фигуру A_n, (а следовательно, и фигуру A). Пересечение B₁, B₂, ... этих полосок, то есть их «предельную фигуру», обозначим через B, она также содержит A, и потому площадь фигуры B не меньше 1/2. Рисунок наглядно показывает, что B является чрезвычайно «извилистой» линией (простой дугой). Эта линия имеет положительную площадь, то есть вряд ли может быть названа «длиной без ширины».

Евклид дает также описание линии как «границы поверхности». Однако и понятие «граница», как мы сейчас увидим, таит в себе много неожиданного. Мы привыкли считать, что к каждому участку линии плоскость примыкает «с двух сторон». Например, если m — простая замкнутая линия, то обе области U и V, определяемые линией m, примыкают к ней на всем ее протяжении (то есть сколь угодно близко к любой точке линии m имеются и точки области U, и точки области V).

Кажется «наглядно очевидным», что линия не может быть совместной границей более чем двух областей на плоскости, которые примыкают к этой линии на всем ее протяжении. Однако здесь интуиция нас обманывает.

Пример 2. Покажем, что на плоскости существует линия, являющаяся совместной границей трех областей. Такие линии обнаружил японский математик Вада.

Предположим, что имеется окруженная морем земля и на ней два озера: теплое и холодное. Для подведения воды от озер и моря к суше проводятся каналы. Для подведения к озерам воды из моря из моря в озера от озер и моря к на суше роются каналы. В первый день от теплого озера отводится канал (не сообщающийся с морской водой и водой холодного озера) так, чтобы не далее чем на расстоянии 1 от каждой точки суши была вода теплого озера (рис. 32.3). Во второй день канал отводится от холодного озера, причем он нигде не сообщается с морем, теплым озером и построенным на день раньше каналом, и работа продолжается до тех пор, пока от каждой точки оставшейся суши не далее чем на расстоянии 1 будет вода холодного озера. В третий день канал таким же порядком отводится от моря.

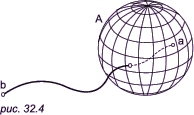
В следующие три дня повторяется то же самое, причем так, чтобы на расстоянии, меньшем 1/2 от каждой точки оставшейся суши, была вода обоих озер и морская вода. В следующие за ними три дня густота сети каналов увеличивается, так что любая вода будет не далее чем на 1/4 от каждой точки оставшейся суши, и так далее. Заметим, что после каждого дня работы оставшаяся суша будет связным куском, так что мы можем покрывать ее в следующие дни еще более плотной сетью каналов.

В пределе мы получим сеть теплой, холодной и морской вод, которые нигде вместе не сливаются. То, что останется от суши, будет уже «линией», причем как угодно близко от любой точки этой линии будет холодная, теплая и морская вода. Иначе говоря, на всем протяжении этой линии к ней будут «примыкать» три области: море с его каналами, холодное озеро с его каналами и теплое озеро с его каналами.

Евклид дает еще и третье описание линии: «поверхность имеет два измерения, линия имеет одно измерение, точка не имеет ни одного измерения». Определить, что такое размерность (число измерений) фигуры, пытались многие математики. Окончательное выяснение смысла этого понятия и создание теории размерности является заслугой замечательного советского математика П. С. Урысона, безвременно погибшего в возрасте 26 лет в 1924 году.

Говорят, что множество A, расположенное в фигуре X, отделяет точку a от точки b, если не существует в фигуре X связного множества, которое содержит точки a и b и не пересекается с A. Например, поверхность шара (сфера) отделяет в пространстве внутренние точки шара от внешних (рис. 32.4). Таким образом, в трехмерном пространстве отделение точек можно производить с помощью двумерных фигур.

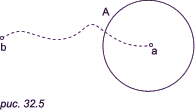
На плоскости (которая представляет собой двумерную фигуру) точку вместе с близкими к ней точками можно отделить от остальных точек с помощью одномерной фигуры (то есть линии, рис. 32.5).

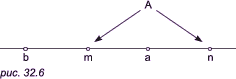
Наконец, на прямой (являющейся одномерной фигурой) точку a вместе с близкими к ней точками можно отделить от остальных точек прямой с помощью фигуры A, состоящей из двух точек m и n (рис. 32.6), то есть с помощью нульмерной фигуры.

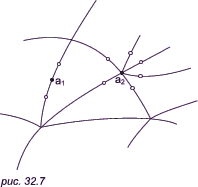
Итак, в фигуре, имеющей n измерений (или, как говорят, в n-мерной фигуре), отделение точки вместе с близкими к ней точками от остальной части фигуры можно производить с помощью фигур, имеющих на одно измерение меньше. Возникает мысль дать определение нульмерных фигур, через них определить одномерные фигуры (линии), затем с помощью одномерных определить двумерные фигуры и так далее.

Будем говорить, что фигура X нульмерна, если в ней не существует никакой связной фигуры, содержащей более одной точки. Например, фигура, состоящая из конечного числа, нульмерна.

Если уже определено, какие фигуры считаются (n - 1)-мерными, то n-мерная фигура определяется как фигура, не являющаяся (n - 1)-мерной, в которой любую точку вместе с близкими к ней точками можно отделить от остальной части фигуры с помощью множества размера n - 1 (или меньше). Это и есть урысоновское определение размерности.

Пример 3. Любой граф является одномерной фигурой, то есть линией. Действительно, точку a вместе с близкими к ней точками можно отделить от остальной части графа конечным нульмерным множеством; отделяющее множество содержит две точки, если a — внутренняя точка ребра (a_i на рис. 32.7), и k точек, если a — вершина индекса k (a₂ на рис. 32.7).

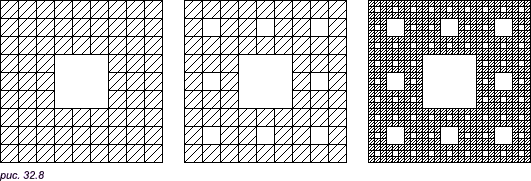
Фигура C является универсальной плоской линией: если линия m вложима в плоскость, то она вложима в плоскость, то она вложима в ковер Серпинского, то есть существует линия m’ c C, гомоморфная m. Ясно, что линии, не вложимые в плоскость, не могут быть вложены в ковер Серпинского. Однако существует в пространстве линия (аналог ковра Серпинского, рис. 32.8), в которую, как доказал австрийский математик Менгер, можно вложить любую линию.

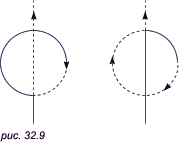
Кривая Пеано

Часто дают еще одно наглядное описание: «Линия есть след движущейся точки». Пусть движущаяся точка пробегает фигуру буквы Ф двумя способами, показанными на рис. 32.9 (сплошной линией указан путь, пройденный в некоторый момент времени, а пунктирной — путь дальнейшего движения). В обоих случаях точка пробегает одно и то же множество, то есть «cлед» движущейся точки одинаков, но пути различны.

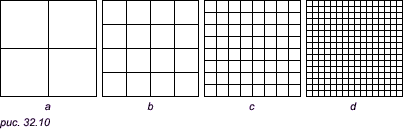
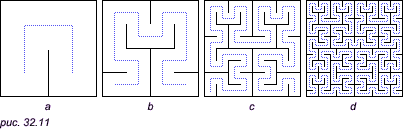
Дадим точное определение понятия дуги. Пусть в некоторой фигуре A с момента времени t = 0 до момента времени t = 1 движется точка. Для любого t известно положение a(t) движущейся точки, то есть каждой точке t отрезка [0, 1] поставлена в соответствие точка a(t), принадлежащая A. Получается отображение отрезка [0, 1] в фигуру A, причем отображение непрерывное, так как точка a(t) «непрерывно» перемещается с изменением t. Это отображение и представляет собой путь. Мы приходим к следующему определению: всякое непрерывное отображение отрезка [0, 1] в фигуру A называется путем (в этой фигуре).

Любую дугу можно представить себе как путь (ведь простая дуга получается с помощью гомоморфного отображения отрезка, а гомоморфное отображение непрерывно). В частности, линию, имеющую «площадь», можно расcматривать как «след движущейся точки». Уже это показывает, что понятие пути является не слишком простым. Следующий пример еще более подтверждает это.

Пример 1. Покажем, что можно построить путь, который проходит каждую точку квадрата. Иными словами, существует непрерывное отображение отрезка на весь квадрат; такие пути называются «кривыми Пеано». Для получения кривой Пеано построим в квадрате Q все более извивающиеся «полоски-лабиринты»: будем делить квадрат на 4, 16, 64, ..., 4ⁿ, ... конгруэнтных квадратиков (рис. 32.10), а затем уберем некоторые из их сторон (рис. 32.11), причем перегородки, оставленные на каком-то этапе построения, сохраняются и на всех последующих.

Средние линии этих полосок (штриховая линия на рис. 32.11) и дадут в пределе путь, заполняющий весь квадрат Q, то есть кривую Пеано. Более точно этот путь можно определить следующим образом. Рассмотрим непрерывное отображение отрезка [0, 1] на первую штриховую ломаную линию (рис. 32.11a), при котором отрезок [0, 1/4] отображается на часть этой ломаной, лежащую в левой нижней четверти большого квадрата, отрезок [1/4, 1/2] — на часть, лежащую в левом верхнем квадрате, а отрезки [1/2, 3/4] и [3/4, 1] — на части, лежащие в правых (верхнем и нижнем) квадратах. Это отображение обозначим через f₁(t) (где 0 <= t <= 1). Далее, через f₂(t) обозначим отображение отрезка [0, 1] на вторую штриховую ломаную ( рис. 32.11b), при котором отрезки [0, 1/16], [1/16, 2/16], ..., [1/16, 2/16] отображаются на последовательные части этой ломаной, лежащие в шестнадцати квадратах второго этапа. Аналогично, f₃(t) будет отображением отрезка [0, 1] на пунктирную ломаную третьего этапа (рис. 32.11c) и так далее.

Предел последовательности функций f₁(t), f₂(t), f₃(t), ... представляет собой отображение f: [0, 1] -> Q, то есть некоторый путь в квадрате Q; это и есть кривая Пеано. Легко пояснить, что этот предел существует. Возьмем, например, точку 1/3 промежутка [0, 1]. Так как 1/3 лежит во второй четверти отрезка [0, 1] (между значениями 1/4 и 1/2), то точка f₁(1/3) лежит в левом верхнем квадрате на рис. 32.10a. Далее, так как 1/3 лежит в интервале [5/16, 6/16], то f₂(1/3) лежит в шестом по порядку квадрате, пробегаемом штриховой ломаной на рис. 32.11b (то есть в левом верхнем квадрате на рис. 32.10b). Так как 1/3 лежит в интервале [21/64, 22/64], то f₃(1/3) лежит в 22-м квадрате, пробегаемом штриховой ломаной на рис. 32.11с (то есть в левом верхнем квадрате на рис. 32.10c), и так далее. Предел этой последовательности уменьшающихся квадратов (вложенных последовательно один в другой) — то есть в данном случае левая верхняя вершина квадрата — и есть точка f(1/3). Таким же образом определяется точка f(t) для любого t из [0, 1].

Заметим, что кривая Пеано не является простой дугой: она имеет бесконечно много «склеиваний» (то есть в квадрате имеется бесконечнo много точек, через которые построенный путь f(t) проходит более, чем один раз).