Рекурсия и фракталы

Рекурсия

Мы говорим, что функция рекурсивна (или что она основана на рекурсии), если в ней содержится одно или несколько обращений к самой себе или к другим функциям, в которых есть обращения к данной функции. При входе в обычную функцию выход из нее всегда происходит раньше, чем повторный вход, но для рекурсивной функции это необязательно.

Приведем пример простой программы TRIANGLS, строящей на экране компьютера изображение вписанных друг в друга треугольников (рис. 24.1) и использующей для этого рекурсивный вызов функции.

Опишем вкратце алгоритм работы программы. Сначала вычерчивается первый треугольник. После этого вызывается функция tria, строящая внутри этого треугольника малый треугольник так, что вершины его лежат точно на серединах сторон большого треугольника. К малому треугольнику с каждой стороны прилегает по треугольнику. Чтобы построить в них точно такую же картину, достаточно рекурсивно вызвать для каждого функцию tria с координатами вершин малых треугольников в качестве аргументов. В обращение включен целочисленный аргумент n, определяющий глубину рекурсии.

Начнем с некоторого целого числа n, заданного пользователем; этот аргумент устанавливается равным n - 1 для каждого из трех рекурсивных обращений. То есть при достижении «самого глубокого уровня рекурсии», значение n становится равным нулю, что приводит к немедленному возврату в вызывающую функцию, то есть в саму функцию tria.

Графика и случайные числа

Иногда нам не нужна полная симметрия, возникающая при прямом применении рекурсии. В таких случаях можно использовать (псевдо-) случайные числа для устранения в некоторой степени такой симметрии. Этим способом с помощью программы TTREE была получена картинка на рис. 24.2.

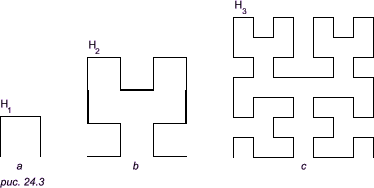
Здесь показано многократное изображение большой буквы T. Точку в нижней части буквы T назовем ее начальной точкой. Начнем с большой буквы T в ее нормальном положении, а концевые точки на верхней горизонтальной полке будут в свою очередь начальными точками новых букв T, несколько меньших, чем первоначальная. От пользователя программы запрашивается ввод двух коэффициентов уменьшения (fx и fy), глубины рекурсии и порогового значения в процентах. После вычерчивания каждой буквы T генерируется случайное число, меньше 100. Если это число меньше, чем заданное пороговое значение, то новая буква T вычерчивается в нормальном положении, в противном случае — в перевернутом. В программе используется хорошо известная формула 1 + r + r² + ... + r^n-1 = (1 - rⁿ)/(1 - r) для вычисления размера первой буквы T, такого, чтобы окончательный результат разместился в пределах границ экрана.

Кривые Гильберта

Рекурсия может быть использована для получения линейного рисунка, известного под названием кривая Гильберта. Кривая Гильберта основана на изображении буквы П, вычерченной в виде трех сторон квадрата, как показано на рис. 24.3a. Существуют кривые Гильберта порядков 1, 2, ..., обозначаемые как H₁, H₂,... На рис. 24.3b изображена кривая порядка H₂, в которой некоторые отрезки прямых линий вычерчены в виде толстых линий. Это так называемые связки (в действительности связки должны иметь одинаковую толщину с другими отрезками, здесь же они показаны утолщенными единственно с целью демонстрации способа получения H₂ из H₁).

Видно, что H₂ можно рассматривать как большую букву П, четыре части которой заменены меньшими по размеру буквами П. Эти меньшие буквы П соединены тремя связками. Каждая сторона меньшей буквы П имеет ту же длину, что и связка, они в три раза меньше стороны квадрата, в который вписывается H₂. Применим ту же процедуру к каждой из четырех букв П, составляющих H₂, то есть каждую букву П в H₂ заменим меньшей H₂, одновременно уменьшим длину связок так, чтобы их длины стали равными длине элементарного отрезка прямой линии, которые содержатся в трех малых фигурах H₂. Таким образом мы получим фигуру H₃, показанную на рис. 24.3с.

Теперь все элементарные отрезки в семь раз меньше, чем длина сторон квадрата, в который вписывается фигура H₃. Отсюда получаем, что коэффициенты уменьшения для этих элементарных отрезков в фигурах H₁, H₂, H₃, ... образуют ряд чисел: 1, 3, 7, ..., то есть в общем случае коэффициент уменьшения для фигуры H_n может быть вычислен по формуле: 2ⁿ - 1.

Заметим, что связки в фигуре H₂ вычерчиваются в тех же направлениях, как и три отрезка, образующие букву П в фигуре H₁. При желании эти последние отрезки прямых линий можно рассматривать как связки, соединяющие четыре точки, которые в свою очередь можно принять за кривую Гильберта нулевого порядка.

В нашей программе HILBERT для построения кривых Гильберта используется рекурсивная функция hilbert со следующими аргументами: координаты точек A, B, C (см. рис. 24.4); горизонтальные и вертикальные компоненты двух направленных связок, причем одна лежит на отрезке AB, а другая — на AC. Они задаются в виде векторов, то есть как пара чисел (dx, dy), где переменные dx и dy могут принимать положительные, нулевые или отрицательные значения, в зависимости от относительного положения точек A, B и C. Эти два вектора в программе обозначаются как dAB и dAC; n — глубина рекурсии, для n = 0 функция ничего не будет делать.

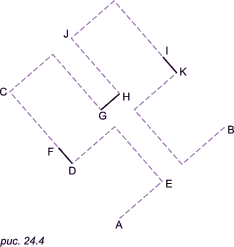
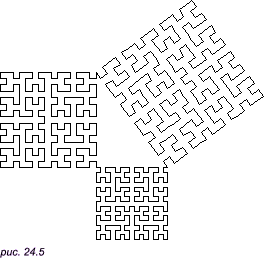
Будем считать, что рис. 24.4 является вариацией изображения буквы П (повернутой на угол 30^o против часовой стрелки), позиция которой целиком определяется тремя заданными точками A, B и C. Будем считать, что точка A является начальной точкой, а точка B — конечной. Основной причиной задания точки C является необходимость указания, с какой стороны от напраленного отрезка AB должна лежать вычерчиваемая кривая. Оба заданных вектора связок dAB и dAC отмечены на рисунке в виде связок в трех местах, а именно как отрезки DF, GH и IK. Три заданные точки A, B, C и два заданных вектора dAB и dAC позволяют определить позиции точек D, E, F, G, H, I, J, K на рисунке. (Мы не будем требовать, чтобы угол CAB был прямым углом или чтобы длина отрезка AB совпадала с длиной отрезка AC, поэтому вместо квадрата каждая буква П может иметь форму произвольного параллелограмма). В общем случае пунктирные линии, показанные на рис. 24.4, фактически не вычерчиваются. Вместо этого мы будем выполнять рекурсивное обращение к нашей функции hilbert для каждой из четырех точечных букв П на рисунке. Для вычерчивания на экране трех отрезков связок DF, GH и IK будем обращаться к нашей функции draw.

На рис. 24.5 представлен результат работы программы.

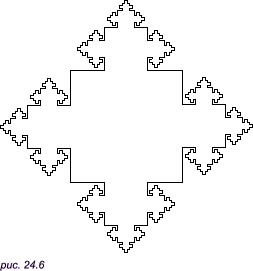
Фракталы

Взгляните на рис. 24.6. На нем представлена замкнутая кривая, которая называется фрактальной кривой или просто фракталом. Фрактал подобен острову с береговой линией, кажущейся ровной издали, но становящейся совершенно нерегулярной по мере приближения. Фигуру, показанную на рис. 24.6, можно построить с помощью рекурсии, причем с увеличении глубины рекурсии мы получим замкнутую область, граница которой становится очень большой по сравнению с самой областью.

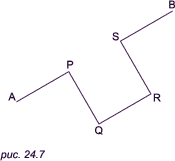
С помощью программы SQFRACT можно получить такую картинку. Первые четыре аргумента функции side программы представляют собой координаты концевых точек A и B отрезка прямой линии. Но этот отрезок будет вычерчен только в том случае, если аргумент n функции side будет равен нулю. В противном случае на этом отрезке будут сформированы две новые точки P и S. Они будут определять концевые точки стороны уменьшенного квадрата (при равенстве PS = f * AB), как показано на (рис. 24.7). Из рисунка очевидно, что координаты точки Q можно вычислить следующим образом:
x_Q = x_P + (y_S - y_P)
y_Q = y_P + (x_S - x_P).

(Напомним, что аналогичный способ формирования новой точки уже обсуждался более подробно при рассмотрении кривой Гильберта). Координаты точки R определяются очень просто, поскольку она находится в таком же отношении к точке Q, как точка S относится к точке P. Теперь можно вычертить отрезок AP, выполнить рекурсивное обращение к функции side для сторон PQ, QR, RS меньшего квадрата и закончить вычерчиванием отрезка SB.

Вместо непосредственного вычерчивания отрезков AP и SB для них можно рекурсивно обратиться к функции side. Хотя в данном конкретном случае это и не дает удовлетворительного результата, но полезна сама идея. Она приводит к целому классу интересных новых кривых, состоящих из отрезков прямых линий, которые, в отличие от рис. 24.6, имеют почти одинаковую длину. (Напомним, что с подобной ситуацией мы встречались в случае кривых Гильберта).

Рассмотрим общую программу FRCURVE для генерации таких кривых. Во-первых, базовая фигура может быть задана либо в виде горизонтального отрезка прямой линии, либо в виде правильного многоугольника. Во-вторых, вместо вычисления позиций новых точек P, Q, R, S («модельных точек») относительно позиций концевых точек A и B, как на рис. 24.7, пользователь в качестве входных данных может задать любое количество таких точек, не обязательно четыре. Введем локальную систему координат, в которой точка A совпадает с точкой начала (0, 0), а точка B — с точкой (1, 0). Тогда позиции модельных точек могут быть выражены в этих локальных координатах. Рассмотрим для примера рис. 24.8, где определены три новые точки с координатами (x, y): (0.45, 0), (0.50, 0.45) и (0.55, 0).

Напомним, что обе концевые точки A(0, 0) и B(1, 0) неявно добавляются к модельным точкам, которые мы должны ввести, поэтому вообще число модельных точек всегда на две точки больше, чем заданное число. Если же всю фигуру целиком применять к каждой из ее четырех частей, то получим рис. 24.9 и так далее.

Поскольку мы можем задать правильный многоугольник, например, с четырьмя сторонами, то программа FRCURVE, в которой реализована эта операция, сформирует изображение, показанное на рис. 24.10.

Программу FRCURVE можно использовать для получения большого разнообразия интересных рисунков. Например, если ввести следующие семь пар чисел, определяющие пары координат по оси x и y для семи модельных точек на единичном интервале, то получим изображение фрактала Минковского.

0.25   0
0.25   0.25
0.5   0.25
0.5   0
0.5   -0.25
0.75   -0.25
0.75   0