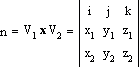Часть I / Лекция 07. Нахождение параметров плоскости

Нахождение плоскости по точкам

Пусть уравнение ax + by + cz + d = 0 описывает плоскость. Переменная d является свободной, ей можно придать любое значение, положим ее равной единице: d = 1. Известно, что плоскость задается, причем однозначным образом, тремя точками (x₁, y₁, z₁), (x₂, y₂, z₂), (x₃, y₃, z₃) пространства (эти точки, вообще говоря, не должны одновременно находиться на одной прямой):

	x1a + y1b + z1c = -1
	x2a + y2b + z2c = -1
	x3a + y3b + z3c = -1

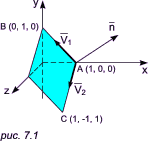
Решив эту систему уравнений относительно неизвестных a, b и c, мы найдем уравнение плоскости. Покажем это на примере. Найдем уравнение плоскости, проходящей через три точки: A(1, 0, 0), B(0, 1, 0), C(1, -1, 1). Рис. 7.1 иллюстрирует нашу задачу:

Представим систему уравнений в виде произведения матриц: первая из них содержит координаты точек A, B и C, вторая — неизвестные a, b и c, третья — правые части уравнений:

Отсюда находим a = -1, b = -1, c = -1 и подставляем их в уравнение плоскости: -1x - 1y - 1z + d = 0 или x + y + z = d. Подставим в это уравнение плоскости любую точку, например, (1, 0, 0) и найдем d: d = 1. Окончательно уравнение данной плоскости выглядит так: x + y + z - 1 = 0.

Метод определения плоскости по нормали

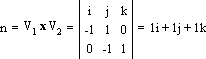
Если имеется возможность определить n — вектор нормали к плоскости, — то можно найти и уравнение этой плоскости; n находится как векторное произведение векторов V₁{x₁, y₁, z₁} и V₂{x₂, y₂, z₂}, лежащих в определяемой плоскости. В координатной форме это запишется следующим образом (значок x обозначает векторное произведение векторов; i, j, k — единичные векторы осей х, у и z):

Для простого примера, приведенного выше, мы будем иметь следующее:
V₁{0 - 1, 1 - 0, 0 - 0} = V₁{-1, 1, 0},
V₂{1 - 1, -1 - 0, 1 - 0} = V₂{0, -1, 1},

Вычисленные коэффициенты при i, j, k подставляем в уравнение плоскости вместо a, b и c: 1x + 1y + 1z + d = 0. Взяв произвольную точку плоскости и подставив ее координаты вместо x, y, z, найдем d: C(1, -1, 1), d = -1 * 1 - 1 * (-1) - 1 * 1 = -1. Итак, окончательное уравнение плоскости примет следующий вид: x + y + z - 1 = 0.

Метод Ньюэла

Этот метод эквивалентен определению нормали в каждой вершине многоугольника посредством векторного произведения прилежащих ребер и усреднения результатов.

Пусть а, b, с, d — коэффициенты уравнения плоскости, тогда:
a = S(y_i - y_j) * (z_i + z_j)
b = S(z_i - z_j) * (x_i + x_j)
c = S(x_i - x_j) * (y_i + y_j)
d = -(ax_n + by_n + cz_n).

Суммирование под знаком суммы ведется по i, которое всюду изменяется от 1 до n, n — число вершин многоугольника. Переменная j принимает значение 1 при i = n, в противном случае j = i + 1. Между точками находим среднюю плоскость, проходящую через все точки. В методе происходит как бы вычисление «центра масс».

Попробуем найти коэффициенты для плоскости, изображенной на рис. 7.1:
a = (y₁ - y₂)(z₁ + z₂) + (y₂ - y₃)(z₂ + z₃) + (y₃ - y₄)(z₃ + z₄) + (y₄ - y₁)(z₄ + z₁) =
= (0 - 1)(0 + 0) + (1 - 0)(0 + 1) + (0 - (-1))(1 + 1) + (-1 - 0)(1 + 0) = 2,
b = ... = 2,
c = ... = 2,
d = -(2x₄ + 2y₄ + 2z₄) = -(2 - 2 + 2) = -2.
Получаем плоскость x + y + z - 1 = 0. Тот же самый результат будет, если вычислить нормали каждой из четырех вершин и усреднить полученные коэффициенты.