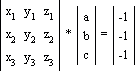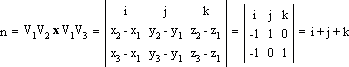Методы определения коэффициентов плоскости

Хотя уравнение плоскости: ax + by + cz + d = 0, содержит четыре неизвестных коэффициента, его можно нормировать так, чтобы свободный коэффициент был равен единице: d = 1. Следовательно, трех неколлинеарных точек достаточно для определения этих коэффициентов. Подстановка координат трех неколлинеарных точек (x₁, y₁, z₁), (x₂, y₂, z₂), (x₃, y₃, z₃) в нормированное уравнение дает:
ax₁ + by₁ + cz₁ = -1
ax₂ + by₂ + cz₂ = -1
ax₃ + by₃ + cz₃ = -1.

В матричной форме это выглядит так:

Или так: |X||C| = |D| (*).

Решение этого уравнения дает значения коэффициентов уравнения плоскости: |C| = |X|^-1|D|.

Другой способ используется, если известен вектор нормали к плоскости, то есть n = ai + bj + ck, где i, j, k — единичные векторы осей x, y, z соответственно. Тогда уравнение плоскости примет вид: ax + by + cz + d = 0.

Величина d вычисляется с помощью произвольной точки на плоскости. В частности, если компоненты этой точки на плоскости (x₁, y₁, z₁), то: d= -(ax₁ + by₁ + cz₁).

Поскольку объем вычислений в алгоритмах удаления невидимых линий или поверхностей растет с увеличением числа многоугольников, для описания поверхностей выгодно использовать многоугольники с более чем тремя сторонами. Эти многоугольники могут быть как невыпуклыми, так и неплоскими. Метод, предложенный Мартином Ньюэлом, позволяет найти как точное решение для уравнений плоскостей, содержащих плоские многоугольники, так и «наилучшее» приближение для неплоских многоугольников. Этот метод эквивалентен определению нормали в каждой вершине многоугольника посредством векторного произведения прилежащих ребер и усреднения результатов. 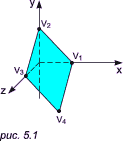Если a, b, c, d — коэффициенты уравнения плоскости, то (здесь n — число вершин многоугольника)
a = S(y_i - y_j)(z_i + z_j)
b = S(z_i - z_j)(x_i + x_j) (**)
c = S(x_i - x_j)(y_i + y_j), где
if i = n then j = 1 else j = i + 1, a d вычисляется с помощью любой точки на плоскости. Этот метод иллюстрируется примером 1.

Пример 1. Уравнения плоскостей. Рассмотрим четырехсторонний плоский многоугольник, описываемый четырьмя вершинами V₁(1, 0, 0), V₂(0, 1, 0), V₃(0, 0, 1) и V₄(1, -1, 1) ( рис. 5.1).

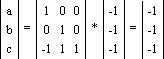
Используя вершины V₁, V₂, V₄ и уравнение (*), получаем:

Или, разрешая относительно коэффициентов уравнения плоскости:

Уравнение плоскости теперь имеет вид:
-x - y - z + 1 = 0 или x + y + z - 1 = 0.

Решая другим методом, можем получить нормаль к этой плоскости, используя векторное произведение пары векторов, являющихся смежными ребрами одной из вершин, например V₁:

i, j, k — единичные векторы осей x, y, z соответственно. Используя уравнение d = -(ax₁ + by₁ + cz₁) и V₄, получаем значение постоянного члена в уравнении плоскости:
d = -1(1 - 1 + 1) = -1.

Следовательно, уравнение плоскости опять имеет вид:
x + y + z - 1 = 0.

Обращаясь теперь к методу Ньюэла при n = 4, получаем из уравнения (**):

a = (y₁ - y₂)(z₁ + z₂) + (y₂ - y₃)(z₂ + z₃) + (y₃ - y₄)(z₃ + z₄) + (y₄ - y₁)(z₄ + z₁) = (-1)(0) + (1)(1) + (1)(2) + (-1)(1) = 2
b = (z₁ - z₂)(x₁ + x₂) + (z₂ - z₃)(x₂ + x₃) + (z₃ - z₄)(x₃ + x₄) + (z₄ - z₁)(x₄ + x₁) = (0)(1) + (-1)(0) + (0)(1) + (1)(2) = 2
c = (x₁ - x₂)(y₁ + y₂) + (x₂ - x₃)(y₂ + y₃) + (x₃ - x₄)(y₃ + y₄) + (x₄ - x₁)(y₄ + y₁) = (1)(1) + (0)(1) + (-1)(-1) + (0)(-1) = 2.

А используя V₄, получаем для постоянного члена:
d = -(2 - 2 + 2) = -2.

После деления на 2 уравнение плоскости вновь принимает вид:
x + y + z - 1 = 0.

Следующий пример проиллюстрирует метод Ньюэла для почти плоских многоугольников.

Пример 2. Неплоские многоугольники. Рассмотрим почти плоский многоугольник, описанный четырьмя вершинами V₁(1, 0, 0), V₂(0, 1, 0), V₃(0, 0, 1) и V₄(1.1, -1, -1). Вычисляя нормаль в каждой вершине через векторное произведение пары прилежащих ребер, имеем:
n₁ = V₁V₂ x V₁V₄ = i + j + 0.9k
n₂ = V₂V₃ x V₂V₁ = i + j + k
n₃ = V₃V₄ x V₃V₂ = i + 1.1j + 1.1k
n₄ = V₄V₁ x V₄V₃ = i + 1.1j + k.

Усредняя эти нормали, получаем:
n = i + 1.05j + k.

Определение постоянного члена в уравнении плоскости с использованием одной из вершин, например V₁, дает d = -1. Следовательно, приближенное уравнение плоскости таково:
x + 1.05y + z - 1 = 0.

Метод Ньюэла приводит к такому же результату. В частности
a = (-1)(0) + (1)(1) + (1)(2) + (-1)(1) = 2
b = (0)(1) + (-1)(0) + (0)(1.1) + (1)(2.1) = 2.1
c = (1)(1) + (0)(1) + (-1.1)(-1) + (0.1)(-1) = 2.

Вычисление d с использованием V₁ и деление на 2 дает такое же приближенное уравнение плоскости. Аппроксимирующая плоскость проходит через прямую x = z и содержит вершины V₁ и V₂. Однако V₂ и V₄ немного смещены по разные стороны от этой плоскости.