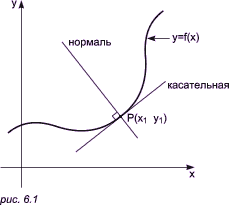
Основные понятия аналитической геометрии на плоскости

Некоторые важные формулы, описывающие отношения между различными геометрическими объектами

Расстояние d между двумя точками (x₁, y₁) и (x₂, y₂) определяется, согласно теореме Пифагора, по следующей формуле: d = [ (x₁ - x₂)² + (y₁ - y₂)² ]^1/2.

Расстояние d между точкой (x₁, y₁) и прямой ax + by + с = 0 определяется формулой d² = (ax₁ + by₁ + c)²/(a² + b²).

Две прямые a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0 пересекаются в точке (x, y), где x = (b₁c₂ - b₂c₁)/(a₁b₂ - a₂b₁) и y = (c₁a₂ - c₂a₁)/(a₁b₂ - a₂b₁), при условии, что a₁b₂ <> a₂b₁; в противном случае эти две прямые параллельны (либо могут совпадать).

Угол q, образованный двумя прямыми a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0, определяется по формуле: cosq = (a₁a₂ + b₁b₂)/[ (a²₁ + b²₁) * (a²₂ + b²₂) ]^1/2.

Две указанные выше прямые параллельны, если a₁b₂ = a₂b₁.

Две прямые, см. выше, перпендикулярны, если a₁a₂ + b₁b₂ = 0.

Пересечения прямых и кривых

Для того чтобы найти точку пересечения двух кривых f(x, y) = 0 и g(x, y) = 0, нужно решить систему этих двух уравнений. Если обе заданные линии прямые, решение находится элементарно, но здесь возможен аномальный случай, когда эти прямые параллельны. Чтобы исключить эту аномалию, необходимо перейти к однородным координатам.

Если f и g являются нелинейными функциями от x и y, решение системы указанных выше уравнений осуществляется при помощи итерационных численных методов.

Касательные и нормали к кривым

Касательная к кривой y = f(x) в точке P(x₁, y₁) определяется уравнением
y = y₁ + f'(x₁)(x - x₁),
где f'(x₁) есть значение производной df/dx в точке x = x₁ (рис. 6.1).

Если рассматриваемая кривая имеет в точке P вертикальную или почти вертикальную касательную, определение касательной при помощи этой формулы невозможно или затруднительно. Затруднения подобного рода легко преодолеваются, если для описания кривой используется неявное уравнение g(x, y) = 0. Тогда неявное уравнение касательной будет иметь вид:
g_x(x₁, y₁)(x - x₁) + g_y(x₁, y₁)(y - y₁) = 0,
где g_x(x₁, y₁) и g_y(x₁, y₁) суть значения производных дg/дx и дg/дy в точке P.

Пример. Касательная к окружности x² + y² - 1 = 0 в точке (1, 0) вычисляется следующим образом.

Поскольку g(x, y) = x² + y² - 1 = 0, то g_x = 2x и g_y = 2y, откуда следует, что g_x(1, 0) = 2 и g_y(1, 0) = 0. Таким образом, уравнение искомой касательной имеет вид 2(x - 1) + 0(y - 0) = 0, то есть касательная является вертикальной линией x = 1. Заметим, что если окружность или касательная записаны в явном виде, получить этот результат невозможно.

Явное выражение для нормали, восстановленной в точке P, имеет вид:
y = y₁ - (x - x₁)/f '(x₁).

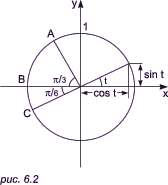
Это уравнение непригодно для случая, когда кривая горизонтальна в точке P. Соответствующее уравнение неявного вида записывается следующим образом:
g_y(x₁, y₁)(x - x₁) - g_x(x₁, y₁)(y - y₁) = 0.

Это уравнение позволяет определять нормали в тех случаях, когда применение явного уравнения невозможно или сопряжено с некоторыми трудностями.

Параметрические уравнения прямых и кривых

Хотя уравнения неявного вида и помогают нам справиться с задачей в случаях, когда применение уравнений явного вида затруднительно или невозможно, они непригодны для непосредственного генерирования точек на кривых, а для определения точек пересечения вынуждают прибегать к численным методам. Существует еще один способ описания прямых и кривых, при котором координаты x и y считаются равноправными: это уравнения параметрического вида.

Например, окружность и многие другие линии имеют свое аналитическое выражение и записываются в разных формах. Нетрудно записать уравнение окружности в явном виде и решить его относительно координат, однако появится неоднозначность в выборе знака перед радикалом. Однако проще представить самые различные линии функциями от некоторого параметра-аргумента, а аргумент сопоставить со временем. При этом линия представляется двумя уравнениями: координаты x и y представляются в виде функций от некоторого вспомогательного параметра t, то есть x = x(t), y = y(t).

Параметрические линии могут быть гораздо более разнообразными, чем описываемые явными уравнениями. Например, параметризация может быть такой, чтобы при равномерном изменении параметра текущая точка с постоянной скоростью двигалась по кривой. Так как такая линия определена полнее, чем обычная, то мы можем различать совпадающие, то есть наложенные друг на друга, линии.

Например, параметрическим способом окружность x² + y² - 1 = 0 записывается в виде уравнений x = cos(t) и y = cos(t) (*), где t принимает значения в интервале 0 <= t < 2p (рис. 6.2). Хотя обычно нужно указывать область изменения параметра t, это может стать преимуществом, если наша цель — описать сегмент кривой. Например, параметрические уравнения (*) и условие 2p/3 <= t <= 7p/6 дают полное описание дуги ABC окружности, представленной на рис. 6.2.

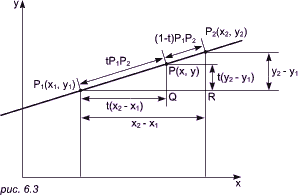
При помощи параметрических уравнений можно, вычисляя x(t) и y(t) для последовательных значений параметра t, получить график кривой.

Если x(t) и y(t) — линейные функции от t, то рассматриваемая кривая будет прямой; в частности, прямая, проходящая через точки P₁(x₁, y₁) и P₂(x₂, y₂), определяется при помощи уравнений
x = x₁ + t(x₂ - x₁)
y = y₁ + t(y₂ - y₁),
где точка P(x, y), как показано на рис. 6.3, делит прямую, соединяющую точки P₁ и P₂, на отрезки в отношении t:(1 - t). Для доказательства этого факта следует использовать подобие треугольников P₁PQ и P₁P₂R.

Прямая ax + by + c = 0 описывается параметрическими уравнениями
x = -ac/(a² + b²) + bt
y = -bc/(a² + b²) - at.

В отличие от неявных (нормированных) уравнений параметрическое представление ни в каком смысле не является единственным, и совершенно различные функции x(t) и y(t) могут представлять одну и ту же кривую. Для полноты информации мы дадим здесь параметрические формулы для касательных и нормалей.

Касательная к кривой x = x(t), y = y(t) в точке P с параметром t = t₁, определяется уравнениями
x = x(t) = x(t₁) + tx'(t₁)
y = y(t) = y(t₁) + ty'(t₁),
где t — параметр на касательной, a x'(t₁), y'(t₁) — значения производных dx/dt и dy/dt в точке t = t₁.

Нормаль, восстановленная к этой кривой, определяется уравнениями
x = x(t₁) + ty'(t₁)
y = y(t₁) + tx'(t₁).

Пересечение двух параметрических кривых

Чтобы найти точку пересечения двух параметрических кривых x = x(t), y = y(t) и x = x(t), y = h(t), нужно решить систему из двух уравнений с двумя неизвестными t и t:
x(t) - x(t) =0
y(t) - h(t) = 0.

Таким образом, здесь ситуация ничуть не лучше, чем в случае, когда кривые описаны при помощи уравнений неявного вида. Если же уравнение одной кривой дано в неявном виде, а другой — в параметрическом, можно параметрическое уравнение подставить в уравнение неявного вида, в результате чего получается одно (как правило нелинейное) уравнение с одной неизвестной t.

Пример. Найдем точки пересечения окружности x² + y² - 1 = 0 и прямой x = t, y = 1 - t. Имеем
t² + (1 - t)² - 1 = 0,
откуда
t² + 1 - 2t + t² - 1 = 0,
2(t² - t) = 0
и t = 0 или 1.

Подставляя этот результат в уравнения параметрического вида, получаем две точки пересечения: (0, 1) и (1, 0).

Если, наоборот, та же самая окружность дана уравнениями параметрического вида x = cos(t), y = sin(t), a прямая определена уравнением неявного вида x + y - 1 = 0, то мы получаем тригонометрическое уравнение cos(t) + sin(t) - 1 = 0.

В этом случае решения t = 0 и t = p/2 очевидны; однако как правило этот метод требует получения численного решения для t. Несмотря на это, мы включили его, чтобы показать, что сложные задачи численного анализа могут решаться проще при помощи смешанных методов.

Кривизна

Радиус кривизны r кривой y = y(x) определяется известной формулой
r = (1 + y'²)^3/2/y'',
где штрих означает дифференцирование по x. Так как радиус кривизны бесконечен в точках перегиба кривой, удобнее пользоваться самой кривизной c = 1/r, поскольку эта величина конечная, если только на кривой нет заострений. Итак,
c = y''/(1 + y'²)^3/2.

Соответствующая формула для кривой, определенной неявным уравнением f(x, y) = 0, имеет вид:
c = - (f_xx * f²_y - 2 * f_xy * f_x * f_y + f_yy * f²_y)/(f²_x + f²_y)^3/2,
где подстрочные индексы x и y означают частное дифференцирование по x и y, например f_xy = д²f/дxдy.

Для кривой, описанной параметрическими уравнениями x = x(t), y = y(t), соответствующее выражение имеет вид:
c = (x'y'' - y'x'')/(x'² + y'²)^3/2,
где точки означают дифференцирование идет по параметру t.