|
Практика 16. Экспертиза проектов
|
| Эксперт | ID |
| Мышкин | 1 |
| Кошкин | 2 |
| Собакин | 3 |
| Лошадкин | 4 |
В своей бригаде выберите предметную область, в которой Вы все компетентны. Примеры областей: шоколад, автомобили, актеры, стили музыки, жанры кино, сорта мороженого, породы собак, …
Старайтесь выбирать область, в которой предпочтения устойчивы, а, значит, имеют смысл. Например, плохим выбором является экспертиза любимых цветов.
Не выбирайте такую область, в которой решения однозначны и все имеют одинаковое мнение (например, количество комнат в квартире).
Создайте единую для всей бригады таблицу оцениваемых экземпляров предметной области (4-6 экземпляров).
Пример.
| ID | А | Б | В | Г |
| Проект | Сливочное | Шоколадное | Пломбир | С колой |
Каждый эксперт самостоятельно назначает приоритеты среди проектов. После этого все эксперты сводят свои мнения в общую таблицу приоритетов.
Пример таблицы приоритетов
| Проекты | А | Б | В | Г |
| Эксперт 1 | 1 | 2 | 3 | 4 |
| Эксперт 2 | 1 | 3 | 2 | 4 |
| Эксперт 3 | 2 | 1 | 3 | 4 |
| Эксперт 4 | 1 | 3 | 4 | 2 |
Проделаем экспертизу мнений несколькими методами.
Метод 1 «Медиана Кемени»
Найдем расстояние между мнением 1 и 2 эксперта. R12=|1-1|+|2-3|+|3-2|+|4-4|=2
Найдите расстояния между мнениями i и j эксперта, перебрав все пары экспертов, и сведите результаты в общую таблицу расстояний.
| Эксперт | 1 | 2 | 3 | 4 |
| 1 | 0 | 2 | 2 | 4 |
| 2 | 2 | 0 | 4 | 4 |
| 3 | 2 | 4 | 0 | 6 |
| 4 | 4 | 4 | 6 | 0 |
Найдем сумму расстояний по строке, которая показывает расстояние от мнения отдельного эксперта до всех остальных членов группы (несогласие с группой).
| Эксперт | Расстояние до группы |
| 1 | 8 |
| 2 | 10 |
| 3 | 12 |
| 4 | 14 |
Выбираем эксперта, который имеет меньше всего разногласий с группой, находится по мнению в середине (медиане) бригады. Места между экспертами распределились так:
| Эксперт | 1 | 2 | 3 | 4 |
| Место | I | II | III | IV |
Первый эксперт занял первое место (у него R=min). Соответственно в качестве ответа принимаются результаты экспертизы первого эксперта, его расклад проектов, а именно:
| Проекты | А | Б | В | Г |
| Место | 1 | 2 | 3 | 4 |
Метод 2 «большинства»
Первое место отдается тому проекту, которому большинство экспертов отдали первое место. Это проект А (ему отдали первое место трое экспертов), он занимает первое место.
Среди оставшихся проектов надо найти проект, которому большинство экспертов отдали второе место. Такого фаворита нет. Пока пропускаем решение о втором месте.
Среди оставшихся проектов надо найти проект, которому большинство экспертов отдали третье место. Такого фаворита нет. Пока пропускаем решение о третьем месте.
Среди оставшихся проектов надо найти проект, которому большинство экспертов отдали четвертое место. Это проект Г, он занимает четвертое место.
Возвращаясь к проектам Б и В и местам 2 и 3. По количеству занявших первое место фаворитом является проект Б, по количеству занявших четвертое место фаворитом является проект В.
Ответ экспертизы методом большинства:
| Проекты | А | Б | В | Г |
| Место | 1 | 2 | 3 | 4 |
Примечание. Любой метод может не сработать. Поэтому экспертизу следует делать несколькими методами.
Метод 3 «Альтернатива Кондорсе»
Для каждой пары проектов (i,j) вычисляем: сколько экспертов Sij отдали предпочтение i-тому проекту перед j-тым.
Например, «проект А лучше проекта Б» считают 3 эксперта (№1,2,4), обратное считает один эксперт (№3). То есть: (SАБ=3)<>(SБА=1)
Продолжая с остальными парами проектов, имеем:
(SАБ=3)<>(SБА=1), то есть А лучше Б
(SАВ=4)<>(SВА=0), то есть А лучше В
(SАГ=4)<>(SГА=0), то есть А лучше Г
(SБВ=3)<>(SВБ=1), то есть Б лучше В
(SБГ=3)<>(SГБ=1), то есть Б лучше Г
(SВГ=3)<>(SГВ=1), то есть В лучше Г
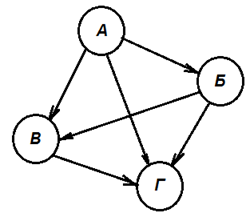
Остается отсортировать результаты, построив граф с вершинами А, Б, В, Г и проводя в нем все связи. Стрелку на связи устанавливаем от лучшего проекта к худшему.
|
|
| Рисунок – Граф предпочтений по результатам экспертизы методом альтернативы Кондорсе |
Приводим граф к ярусно-параллельной форме (ЯПФ). На первый верхний ярус устанавливаем такую вершину, в которую не входят никакие стрелки.
На второй ярус устанавливаем такую вершину, в которую входит только стрелка связи от вершины первого яруса, остальные стрелки, исходящие из вершины второго яруса, ведут вниз, к вершинам более низких ярусов. И так далее.
Очевидно, что в ЯПФ-графе стрелки связей идут строго сверху вниз.
|
|
| Рисунок – Граф в ярусно-параллельной форме (пример) |
Ответ экспертизы методом альтернативы Кондорсе:
| Проекты | А | Б | В | Г |
| Место | 1 | 2 | 3 | 4 |
Метод 4 «Борда»
Подсчитаем количество штрафных баллов, полученных каждым проектом от всех экспертов.
| Проекты | А | Б | В | Г |
| Эксперт 1 | 1 | 2 | 3 | 4 |
| Эксперт 2 | 1 | 3 | 2 | 4 |
| Эксперт 3 | 2 | 1 | 3 | 4 |
| Эксперт 4 | 1 | 3 | 4 | 2 |
| Сумма баллов | 5 | 9 | 12 | 14 |
Проект, который получил минимум штрафных баллов, считается на первом месте. И так далее, сортируя проекты по числу баллов.
Ответ экспертизы, полученный методом Борда:
| Проекты | А | Б | В | Г |
| Место | 1 | 2 | 3 | 4 |
Сводим результаты экспертизы, полученные разными методами, воедино:
| Проекты | А | Б | В | Г |
| Метод Кемени | 1 | 2 | 3 | 4 |
| Метод большинства | 1 | 2 | 3 | 4 |
| Метод Альтернативы Кондорсе | 1 | 2 | 3 | 4 |
| Метод Борда | 1 | 2 | 3 | 4 |
Окончательный результат экспертизы U:
| Проекты | А | Б | В | Г |
| Место | 1 | 2 | 3 | 4 |
Примечание. Рассмотренные методы отражают законы, которые не наблюдаются в природе, то есть субъективны, а, значит, могут показывать разный результат на одном и том же наборе исходных данных. Поэтому необходимо проводить экспертизу несколькими методами, выводя общий средний результат.
Заодно отметим, что методы дают близкий результат друг к другу и все-таки имеют некоторую долю объективности.
Проверка результата экспертизы бригады
Проведем две проверки: степень согласия группы и оценка объективности каждого эксперта.
Проверка степени согласия бригады
| Проекты | А | Б | В | Г | |
| Эксперт 1 | 1 | 2 | 3 | 4 | |
| Эксперт 2 | 1 | 3 | 2 | 4 | |
| Эксперт 3 | 2 | 1 | 3 | 4 | |
| Эксперт 4 | 1 | 3 | 4 | 2 | |
| Сумма баллов | 5 | 9 | 12 | 14 | Средний балл проекта: (5+9+12+14)/4=10 |
| Разброс баллов | -5 | -1 | 2 | 4 | |
| Квадрат разброса | 25 | 1 | 4 | 16 | Сумма: 46 D=46 |
Количество экспертов, n=4.
Количество проектов, m=4.
При полном согласии экспертов W=1, при полной несогласованности экспертов: W=0.
Проверка на объективность экспертов
Ai = 1 – D(Эi, U)/∑D(Эj,U), где D – расстояние между мнением вычисляемого эксперта и результатом экспертизы бригады U, ∑D – сумма всех расстояний от каждого эксперта до результата бригады U.
| Проекты | А | Б | В | Г | Разность между мнением эксперта Di и результатом группы U |
| Эксперт 1 | 1 | 2 | 3 | 4 | 0 |
| Эксперт 2 | 1 | 3 | 2 | 4 | 2 |
| Эксперт 3 | 2 | 1 | 3 | 4 | 2 |
| Эксперт 4 | 1 | 3 | 4 | 2 | 4 |
| U | 1 | 2 | 3 | 4 | Сумма разностей мнений: 8 |
А1 = 1 – (|1-1|+|2-2|+|3-3|+|4-4|)/8 = 1
A2 = 1 – (|1-1|+|3-2|+|2-3|+|4-4|)/8 = 0.75
A3 = 1 – (|2-1|+|1-2|+|3-3|+|4-4|)/8 = 0.75
A4 = 1 – (|1-1|+|2-2|+|4-3|+|2-4|)/8 = 0.5
Менее объективным (компетентным) оказался эксперт №4, самым компетентным – эксперт №1.
В отчете представьте решения экспертизы четырьмя методами, результат экспертизы и его проверки.
Задание 2
Прочитайте лекцию «Экспертиза» - метод Дельфы.
Метод Дельфы применяется в случае, если предметная область такова, что мнения экспертов не могут быть учтены. Например, выбор жены.
Изучите метод и пример, рассмотренный в лекции. Выберите свою предметную область и сформулируйте свой пример из этой области. Примените метод Дельфы и проведите экспертизу.
Обратите внимание, что метод Дельфы - итерационный. Необходимо плавно снижать порог принятия решения до момента, когда граф становится ЯПФ. В этот момент граф становится решением экспертизы.
В отчете представьте описание примера, промежуточные итерации и результат экспертизы.
| О руководителе курса «Моделирование систем» | Лекция 02. Линейные регрессионные модели | ||||||||||||||||
|
|||||||||||||||||