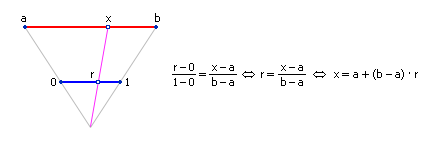Практика 12. Моделирование потоков случайных событий

Теория

На практике часто необходимо узнать не только какие события происходят и сколько, но и когда происходит очередное событие. События образуют поток событий. Естественно, надо наблюдать за однородными событиями. Например, выезд машины скорой помощи со станции, прибытие самолетов в аэропорт, появление покупателей на кассе магазина. Если рассмотреть время прихода события, то поток можно отобразить на оси времени в виде последовательности отдельных точек. Одна точка – одно событие.

Рисунок – Случайные события в потоке

Характеристикой потока является интенсивность потока: редкие события – маленькое значение интенсивности, частые события – большое значение интенсивности потока.

Интенсивность потока λ — это среднее число событий в единицу времени. Интенсивность потока можно рассчитать экспериментально по формуле: λ = N/T_н, где N — число событий, произошедших за время наблюдения T_н.

Если интервал между событиями τ_j равен константе или определен какой-либо формулой в виде: t_j = f(t_j – 1), то поток называется детерминированным. Иначе поток называется случайным.

За эталон потока в моделировании принято брать пуассоновский поток.

Пуассоновский поток – ординарный, без последействия. Мы рассмотрим еще и стационарный поток, то есть простейший.

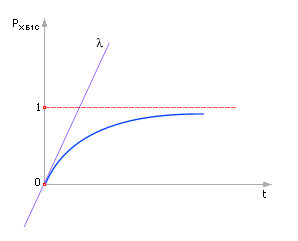
Рисунок – График изменения вероятности хотя бы одного события со временем t

Из графика видно, что вероятность появления хотя бы одного события стремится со временем к единице, то есть при соответствующем длительном наблюдении события таковое обязательно рано или поздно произойдет. Чем дольше мы наблюдаем за событием (чем более t), тем больше вероятность того, что событие произойдет — график функции монотонно возрастает.

Чем больше интенсивность появления события (чем больше λ), тем быстрее наступает это событие, и тем быстрее функция стремится к единице. На графике параметр λ представлен крутизной линии (наклон касательной).

Если увеличивать λ, то при наблюдении за событием в течение одного и того же времени τ, вероятность наступления события возрастает. Очевидно, что график исходит из 0, так как если время наблюдения бесконечно мало, то вероятность того, что событие произойдет за это время, ничтожна. И наоборот, если время наблюдения бесконечно велико, то событие обязательно произойдет хотя бы один раз, значит, график стремится к значению вероятности равной 1.

Рисунок – Зависимости вероятности совершения хотя бы одного события со временем для различных значений интенсивности потока λ

Так как 0 <= P <= 1 и 0 <= (1-r) <= 1, то, выражая r, имеем формулу для разыгрывания интервала между двумя случайными событиями:

τ = –1/λ • Ln(r).

Пример 1

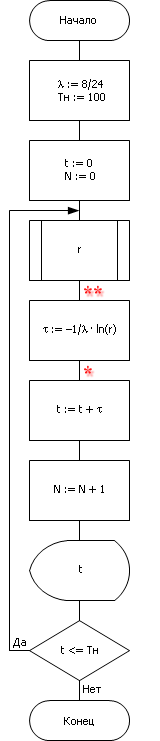
Рассмотрим поток изделий, приходящих на технологическую операцию. Изделия приходят случайным образом — в среднем восемь штук за сутки (интенсивность потока λ = 8/24 [ед/час]). Необходимо промоделировать этот процесс в течение T_н = 100 часов. m = 1/λ = 24/8 = 3, то есть в среднем одна деталь за три часа. Заметим, что σ = 3. На рисунке представлен алгоритм, генерирующий поток случайных событий.

Рисунок – Блок-схема генерации случайных событий

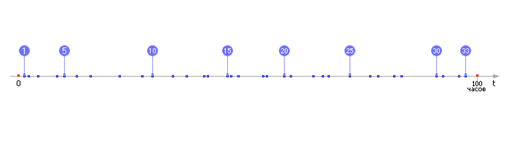
На рисунке показан результат работы алгоритма — моменты времени, когда детали приходили на операцию. Как видно, всего за период T_н = 100 производственный узел обработал N = 33 изделия. Если запустить алгоритм снова, то N может оказаться равным, например, 34, 35 или 32. Но в среднем, за K прогонов алгоритма N будет равно 33.33… Если посчитать расстояния между событиями t_сi и моментами времени, определяемыми как 3 • i, то в среднем величина будет равна σ = 3.

Рисунок – Сгенерированные случайные события в простейшем потоке

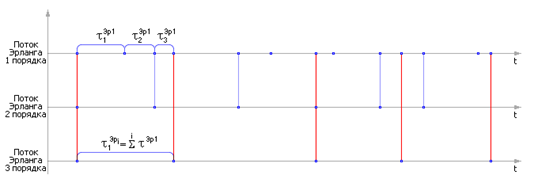
Поток Эрланга k-го порядка — это поток случайных событий, получающийся, если в простейшем случайном потоке сохранить каждое k-е событие, а остальные отбросить. Порядок потока — мера последействия потока. То есть обратной величиной к мере случайности потока является его порядок.

Рисунок – Распределение случайных событий в потоках Эрланга

Получение потока Эрланга базируется на Центральной предельной теореме – сумма случайных величин есть величина неслучайная. Чем больше слагаемых, тем менее случайной является их сумма. То есть поток становится детерминированным. Так можно управлять случайностью.

Задание 1

Смоделируйте последовательность случайных событий с потоком, равным 9 штук в час с точностью 90%.

Разыгрываем последовательность случайных чисел, равномерно распределенных в интервале [0,1] любым ранее рассмотренным ранее способом.

По формуле τ = –1/9 • Ln(r) преобразуем полученные числа в последовательность временных интервалов.

Начертите горизонтальную прямую - ось времени - и выберите масштаб изображения: клеток в час. Разметьте ось в выбранном масштабе.

На оси времени отложите от нуля вправо первый интервал времени длиной τ в выбранном масштабе времени, установите отметку «1» на конце интервала. От отметки «1» отложите второй интервал соответствующей длины вдоль оси в выбранном масштабе. Поставьте в конце второго интервала отметку «2». Продолжите данную процедуру для остальных сгенерированных интервалов.

Ответим на вопрос, сколько надо использовать интервалов (случайных событий) для достижения точности моделирования 90%.

Проведите вертикальную линию в конце первого часа. Подсчитайте по отметкам количество событий N, которое прошло за данный час: N/1 [шт./час].

Отложите на графике «Среднее число событий за час в зависимости от времени моделирования» точку с координатами (1 час, N/1). Передвигая вертикальную черту каждый раз на 1 час далее и повторяя процедуру измерения количества событий N, попавших в этот измеряемый интервал Т, ставьте точку на график по координатам: (Т, N/T).

По мере увеличения времени моделирования график начнет успокаиваться. Дождитесь момента, когда график зайдет в трубку ошибок ±10%, то есть ±0,1 от уровня N/Т, и больше не выйдет оттуда никогда, и определите критическое время моделирования Ткр.

В реальности процесс моделирования продолжают до момента 2Ткр.

Насколько близко полученное значение к числу «9» к моменту 2Ткр?

В тетради приведите таблицу случайных чисел, временную ось с отметками случайных событий, статистический график, ответ и вывод.

Напишите процедуру, моделирующую данный процесс.

Задание 2 (по желанию)

Смоделируйте поток прибытия вагонов на железнодорожную станцию.

Поезда прибывают на станцию в среднем 6 штук в час. В каждом поезде содержится от 8 до 20 вагонов (включая локомотив). Количество вагонов подчиняется равномерному распределению.

Частота прохода поездов через станцию меняется: с 6-00 до 24-00 поезда идут 8 штук в час, с 0-00 до 6-00 4 штуки в час.

Стоянка каждого поезда на станции – 10 минут.

На станции имеется два параллельных железнодорожных пути длиной 20 вагонов. Определите задержку поездов из-за невозможности въезда их на станцию. (Сумма интервалов задержек всех поездов за все время наблюдения, деленная на время наблюдения). Поезда ожидают своей очереди на подъездных путях друг за другом. Подъездные пути можно считать бесконечными и имеющими две нитки (въезд и выезд со станции). Поезд может подойти как с одной стороны станции, так и с другой (равномерно случайно).

Точность расчета – 80%.

Обратите внимание, что поток вагонов не является стационарным и ординарным.

Указания

Разыгрываем последовательность случайных чисел от стандартного ГСЧрр[0,1] любым способом.

Масштабируем и сдвигаем часть чисел в интервал [8,20], которые будут имитировать количество вагонов А в железнодорожном составе по формуле:

Рисунок – Схема масштабирования чисел

По формуле τ = –1/8 • Ln(r) заготавливаем случайные числа – временные интервалы (в долях часа) В между приходами поездов в дневное время.

По формуле τ = –1/4 • Ln(r) заготавливаем случайные числа – временные интервалы (в долях часа) В между поездами в ночное время.

Определяем для каждой пары чисел А и В признак Р, откуда прибывает поезд, разыгрывая равномерным ГСЧ случайные числа: если r<0.5, то поезд слева, Р=Левый, если r>=0.5, то поезд справа, Р=Правый.

Числа А, В, Р удобно записать в столбцы построчно в две таблицы «День», «Ночь».

Случайные числа в таблицах не должны использоваться повторно.

Поскольку расчет идет в часах, то 10 минут – это 10/60 = 0,167 часа.

Имитируем приход и отъезд поездов со станции на временных шкалах, заготовив счетчики количества стоящих вагонов на каждом из двух путей станции и счетчики-вектора вагонов слева и справа от станции.

Время прибытия поезда на станцию рассчитаем по формуле: t:=t+τ.

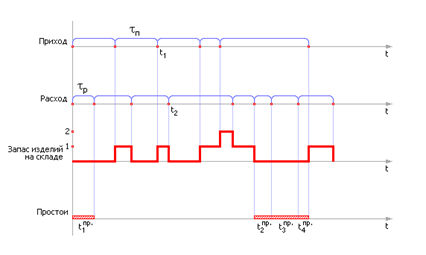
Строим временную диаграмму, подобную изображенной на рисунке, используя сгенерированные числа. Для наглядности начертите горизонтальные параллельные прямые линии: 1 путь, 2 путь, поезда слева, поезда справа.

Заранее выберите масштаб изображения: клеток в час.

Рисунок – Графики моделирования количества изделий на складе

После моделирования снимите статистику ожиданий поездов на подъездных путях, указывая слагаемые в таблицах во время моделирования.

На основе снятой статистики получите ответ.

Рекомендация: получите ответ несколько раз в зависимости от смоделированных поездов. Постройте график улучшения ответа, определите момент успокоения графика на 80%. Дайте окончательный ответ с точностью 80%

К следующему разу каждому студенту подготовить 1 лист миллиметровой бумаги. Разрезать лист миллиметровки вдоль его длинной стороны ровно пополам и склеить по малой его стороне в одну длинную ленту, соблюдая неизменным шаг миллиметровки.

Договориться с другими студентами: о сотрудничестве в коллективе для выполнения общей инженерной работы по расчету системы массового обслуживания. Состав коллектива - 3-4 студента.