Практика 8. Моделирование нелинейностей и конструктивных особенностей

Пример модели статической системы. Логические функции. Для начала рассмотрим простую нелинейность релейного типа и допустим, что функция Y(X) обратима. Такие зависимости называют статическими (значение на входе X однозначно, не зависимо от предыстории процесса определяет значение на выходе Y). Многие производственные процессы могут быть описаны таким способом.

Например, пусть зависимость состоит из трех участков (см. рисунок). Часто характерной особенностью таких зависимостей является наличие в них участка, блокирующего выход, линейного участка и участка насыщения. Первый участок указывает на то, что, не подавая сырья (X = 0) на вход производственного процесса, нельзя надеяться на какой-либо результат (Y = 0). Второй участок указывает на тот факт, что, увеличивая количество сырья на входе, мы обеспечиваем увеличение готовой продукции на выходе. И, наконец, понятно, что если сырья будет очень много (Y >> 0), то какие-либо ограничения производственного процесса (например, производительность оборудования, квалификация персонала, финансовые, энергетические ресурсы) все равно не позволят переработать все это сырье и выпустить соответствующее количество продукции. В сложных системах такой участок насыщения присутствует обязательно.

Рисунок - Зависимость релейного типа

Обратите внимание на то, что каждый из участков можно легко описать в отдельности. Представленная на рисунке зависимость математически описывается тремя функциями. Три строки в записи означают, что в каждый отдельный момент (то есть, при определенном значении X) из описания используется одна из строк (первая, вторая или третья). То есть подразумевается (но явно не записывается), что строки соединены знаком ИЛИ. Когда имеют дело с вычислительной техникой и языками программирования, где умалчивать — опасно, эту конструкцию записывают в строку:

Y := (0 при X ≤ 0) ИЛИ (X • c/b при 0 < X ≤ b) ИЛИ (c при X > b).

Если процессы аналоговые, то есть если мы имеем дело с любыми (рациональными) значениями Х, роль операции ИЛИ играет знак «+»:

Y := (0 при X ≤ 0) + (X • c/b при 0 < X ≤ b) + (c при X > b).

В самом деле: если условия исключают друг друга, то в любой момент времени может реализоваться только одно из трех условий. Оно и даст требуемый ответ в сумму. От остальных слагаемых в сумму придет ноль. Сложение искомого значения с нолями сформирует правильный ответ в целом.

Рассмотрим теперь отдельно одну из конструкций, например, c при X > b. Ее использование означает следующую фразу (которую не пишут и не произносят полностью исключительно в целях экономии места и времени): «если X больше b, то Y присвоить c». Воспользуемся единичной функцией Хевисайда (см. рисунок) для перевода данной фразы на формальный язык. Напомним, что значение единичной функции равно 0, если ее аргумент меньше или равен 0, и равно 1, если ее аргумент больше 0.

Рисунок - Единичная функция Хевисайда Y = ed(X) или Y=one(X)

В результате получим: Y := c • ed(X – b). Проверим полученную формулу. Действительно:

• если X < b, то аргумент (X – b) единичной функции отрицателен, следовательно, сама функция равна 0, поэтому Y = 0;
• если X = b, то аргумент (X – b) единичной функции равен нулю, следовательно, сама функция равна 0, поэтому Y = 0;
• если X > b, то аргумент (X – b) единичной функции положителен, следовательно, сама функция равна 1, поэтому Y = c.

Заметим, что в нашей формуле Y := c • ed(X – b) знак умножения играет роль логического И, поскольку для получения окончательного результата нам, во-первых, требуется значение «c» И, во-вторых, чтобы истиной (то есть, единицей) было значение выражения ed(X – b).

Как видите, словесная логическая конструкция

если Условие, то Искомая_величина := Факт

соответствует типовой математической конструкции

Искомая_величина := Факт • ed(Условие).

ВАЖНО! Итак, неравенство превращается в единичную функцию (в математике единичная функция эквивалентна понятию ПРЕДИКАТ), логическое ИЛИ заменяется на знак сложения, логическое И заменяется на знак умножения. Знак «:=» выражает причинно-следственную связь, увязывая причину и следствие в явном виде. В случае неявного задания функции роль этого знака будет играть знак уравнивания «=».

Теперь переведем вторую часть выражения, Y := X • c/b при 0 < X ≤ b, на формальный язык: Y := X • c/b • ed(X) • ed(b – X). Заметим, что правильный результат получится, если будет соблюдено уже три условия одновременно: (X • c/b) И (X > 0) И (X ≤ b). Так же поступим и с оставшейся частью: Y := 0 при 0 ≤ X. Формальный перевод имеет вид: Y := 0 • ed(0 – X).

Собирая все три части вместе, имеем:

Y := 0 • ed(0 – X) + X • c/b • ed(X) • ed(b – X) + c • ed(X – b).

Обратите внимание, что первое слагаемое вообще-то можно не писать, так как оно всегда равно 0. Остается:

Y := X • c/b • ed(X) • ed(b – X) + c • ed(X – b).

Еще одно замечание. Если протестировать функцию в точке X = b, то окажется, что и первое слагаемое, и второе одновременно равны 0, а вся функция будет иметь вид, показанный на рисунке. Такая ситуация называется прощелкой. (А есть ли прощелка между 0 • ed(0 – X) и X • c/b • ed(X) • ed(b – X)? Если «да», то при каком X? Проверьте себя.)

Рисунок - Вид логической функции с ошибкой типа прощелки в описании

Чтобы избежать прощелок, надо писать формулы аккуратнее:

Y := X • c/b • ed(X) • not(ed(X – b)) + c • ed(X – b).

Действительно, в этом случае либо not(ed(X – b)) (из первого слагаемого), либо ed(X – b) (из второго слагаемого) окажется обязательно равным 1, и прощелка исчезнет. Заметим, что можно не вводить дополнительную операцию not(q), а использовать ее аналог: 1 – ed(q).

Итак, обобщим: если в записи зависимости имеется n отрезков и при этом X на i-ом отрезке удовлетворяет условию: a_i < X ≤ a_{i + 1}, то имеем:

Обратите внимание. Функция получилась однозначной, то есть одному и тому же X всегда соответствует одно и то же Y . Удобство таких описаний в том, что Y вычисляется в любой момент для любого X , достаточно подставить нужное любое значение X в формулу.

Вид записи зависит от системы, которой придется исполнять такую запись. Если система не понимает запись, то она не сможет ее исполнить, и такая запись бесполезна. Язык такой мертв и ничего не означает, так как не служит средством коммуникации, передачи информации от одного агента другому. (Забегая вперед, отметим, что у языка есть и еще другие функции, например, способность манипуляции объектами, которые он описывает, функция исчисления.) К примеру, если исполнителем является алгоритмическая машина, то конструкция

Y := X • c/b • ed(X) • not(ed(X – b)) + c • ed(X – b).

будет иметь вид, показанный на рисунке.

Рисунок - Алгоритмическая реализация производственных моделей в виде логических функций с использованием условных конструкций

Как видите, есть соответствие в языках описания. Условная конструкция в алгоритмах соответствует «многоэтажной» формуле в математике или конструкции

в формализованном языке моделирования. Или, с использованием логических функций И, ИЛИ, НЕ:

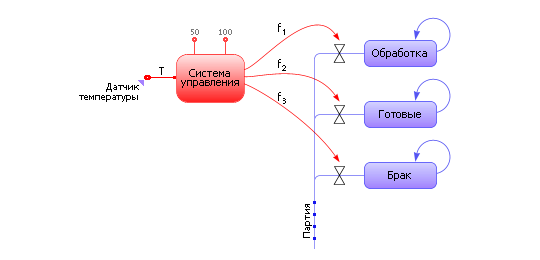
Пример модели динамической системы. Обработка партии изделий в термической печи.

Рассмотрим обработку партии изделий в термической печи. Если температура в печи до 50 градусов, то партия снова поступает в обработку. Если температура в печи между 50 и 100 градусами, то партия уходит на склад готовых изделий. Если температура в печи больше 100 градусов, то партия поступает в брак.

Блок информационных сигналов имеет вид:

f₁ := ed(50 – T);

f₂ := not(ed(50 – T)) • ed(100 – T);

f₃ := not(ed(100 – T)).

Блок имитации материальных процессов:

Обр := Партия • f₁;

Готовые := Готовые + Партия • f₂;

Брак := Брак + Партия • f₃.

Обратите внимание: на схеме модели (рисунок) отдельно сформированы все возможные и существенные для процесса условия «ed(Условие)», отдельно сформированы информационные сигналы (f₁, f₂, f₃), отдельно описаны материальные потоки.

Рисунок - Схема модели «Обработка изделий в термической печи»

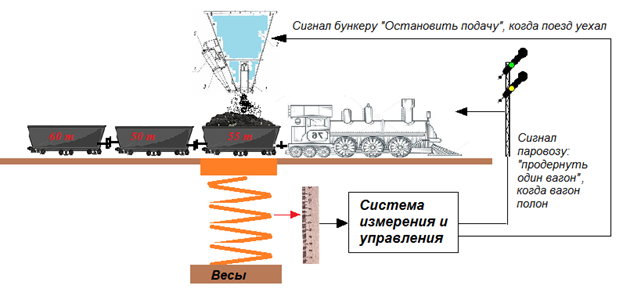
Задание 1

Построить модель системы управления погрузкой поезда.

Рисунок – Схема системы управления погрузкой поезда