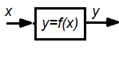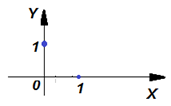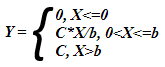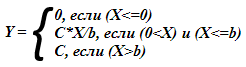Практика 4. Моделирование функций, технических устройств и процессов

Теория

Обычные функции Y=f(X) в программировании реализуются конструкцией вычислительного оператора.

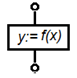
В технической нотации:

Рассмотрим более сложную математическую конструкцию:

Y=f(X)

Z=g(Y)

Или как систему уравнений:

Или как композицию: Z=g(f(X)).

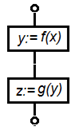
Последовательность функций в программировании описывается «точкой с запятой», в блок-схеме – последовательностью вычислительных блоков.

В технике последовательность (а точнее «композиция») функций представляется как каскад блоков:

В науке и технике широко используют функцию Хэвисайда для конструирования различного рода функций и выражений.

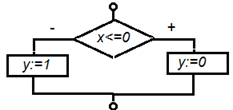
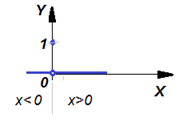
Функция Хэвисайда принимает значения ноль, если ее аргумент меньше нуля, и принимает значение единица, если ее аргумент не меньше нуля. В программировании функция Хэвисайда аналогична условному оператору if (ЕСЛИ):

ЕСЛИ (X<=0) ТО (Y:=0) ИНАЧЕ (Y:=1)
If (x<=0) then y:=0; else y:=1;

Однако функция Хэвисайда удобнее условного оператора, так как позволяет работать с ней методами классической математики – брать производную, интегрировать, решать уравнения, брать обратную функцию, комбинировать с другими функциями, осуществлять композицию функций, складывать и т.д. .

В литературе функция Хэвисайда обозначается Y=one(X), или Y=1[X], или Y=ed(X).

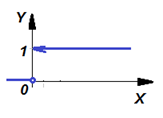
По определению функция Хэвисайда:

имеет график:

Рисунок – График функции Хэвисайда, Y=one(X) или 1(X)

Примечание: в различных приложениях значение Y в точке X=0 принимают как 0, так и 1 (в зависимости от вкусов автора).

Полезными инструментами являются также функция Дирака, которая является производной функции Хэвисайда. Функция Дирака называется «дельта»-функцией, обозначается: Y=delta(X) или Y=δ(Х).

Рисунок – График функции Дирака, Y=delta(X)

Полезной также является функция Y=not(X).

Рисунок – График функции Y=not(X)

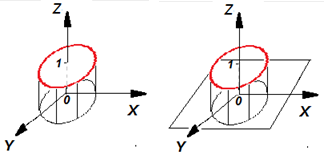
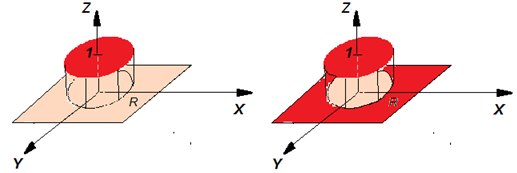
Функция (Y=f(X)) всегда превращается в уравнение (Y-f(X)=0), но уравнение не всегда записывается в виде функции. Например, уравнение окружности (Y²+X²=R²) после выражения Y через Х имеет вид: Y=±√(R²-X²). На графике видно, что одному значению Х соответствует 2 значения Y, что противоречит функции по ее определению.

Если использовать функции Дирака и Хэвисайда, то запись будет корректной:

Z = δ(X² + Y² - R²) – на границе,

Z = one(R² - X² - Y²) – во внутренней области окружности: X²+Y²<R²

Задание 1

На графике изображена однозначная ломаная линия. Напишите аналитическую функцию, реализующую модель графика.

Рисунок – График ломаной однозначной функции

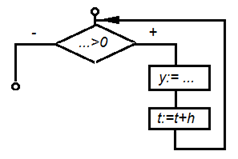
В программировании модель такой функции можно реализовать:

Рисунок – Структура, реализующая модель ломаной однозначной функции

Математик традиционно запишет такую функцию так:

Или так:

Сразу заметим, что работать с такой записью сложно.

1. Не ясен смысл фигурной скобки.

2. Не ясен смысл слова ЕСЛИ.

3. Запись имеет вид несколько этажей.

4. Не ясен смысл запятых.

5. Запись содержит неравенства, с которыми аналитически трудно работать.

6. Записью оперировать в математических выкладках внутри других выражений не удобно.

7. Запись (не в одну строчку) крайне неудобна при компьютерном наборе текста.

8. Не ясно, как брать производные, интегралы, композицию, обратную и другие операции. Текст начинает разбиваться на множество случаев и словесных рассуждений.

9. Вся математика двигалась резко вперед, если вводилась формальная однозначная запись вместо слов и, более того, компактная запись - знак. (Традицию современной математической записи положил Виет, основоположник символической алгебры).

Поэтому попробуем записать такую функцию в одну строку, соблюдая точность и однозначное прочтение всех ее знаков: Y := (0 И (X<=0)) ИЛИ ((c*X/b) И (X>0) И (X<=b)) ИЛИ (c И (X>b))

Избавляясь от знаков «И», «ИЛИ»:

Y := 0*(X<=0) + (c*X/b)*(X>0)*(X<=b) + c* (X>b)

или

Y := (c*X/b)*(X>0)*(X<=b) + c* (X>b), именно так, в принципе, запишет функцию программист на языке СИ++ и получит правильный результат после ее выполнения.

Теперь избавимся от знаков неравенств, с которыми трудно работать:

Y := (c*X/b)*one(X)*one(b-X) +c*(1-one(b-X))

С функцией в такой записи позволяются любые математические операции!!

Обобщая сказанное для функций аналогичного типа, запишем:

Y := ИЛИ (Значение i) И (Условие i) по индексу i

(Знак «ИЛИ» означает тоже, что и знак суммы ∑)

Y := ∑(Значение i)*(Условие i) по индексу i

Y := ∑A_i * one(B_i-X)*one(X-C_i) по индексу i

Задание 2

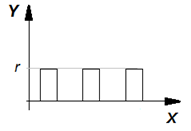
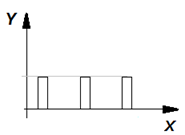
Смоделируйте периодическую бесконечно повторяющуюся функцию, изображенную на графике:

В программировании модель реализуется циклической структурой:

Опишите модель в математической однострочной нотации. Приведите ее аналог в виде схемы технического устройства.

Задание 3

Смоделируйте функцию с произвольной скважностью. Скважность – отношение времени ненулевого сигнала к величине периода функции.

Задание 4

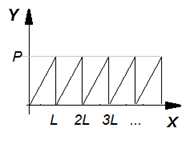
Смоделируйте пилообразную периодическую функцию, изображенную на графике.

Задание 5

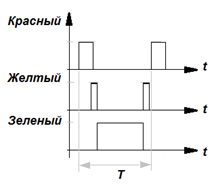
Смоделируйте модель работы светофора, у которого заданы время горения красного, желтого и зеленого света.

Задание 6

Смоделируйте работу коммутатора, который в разные моменты времени поочередно передает входной сигнал на одну из трех выходных линий. Работа коммутатора повторяется периодически и бесконечно.

Задание 7

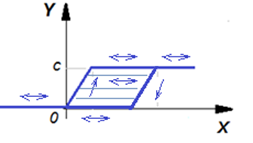
Смоделируйте функцию «гистерезис», вид ее изображен на графике. Функция неоднозначна в своей средней области.

Обратите внимание: в средней области функция, имеющая координаты (X,Y), может перемещаться как вперед (увеличивая значение Х), так и назад (уменьшая значение Х). На границах области такое поведение невозможно.

Задание 8

Нарисуйте произвольную функцию, ограниченную на участке 0<=X<=T и периодически повторяемую далее. Представьте функцию в виде ряда Фурье. Представьте функцию в виде полиномиального ряда.

Задание 9

Реализуйте из типовых элементов модель елочной гирлянды, замкнутой в кольцо. Гирлянда должна передавать сигнал от одной лампы к другой с заданной задержкой. При создании конструктора минимизируйте количество его элементов при этом обеспечьте максимальное разнообразие реализуемых собираемых схем систем.

Задание 10

Напишите уравнение системы.

Печь обрабатывает изделия. Если изделие находится в печи от 10 до 12 минут при температуре от 100 до 110 градусов, то изделие считается готовым. Если условие не выполняется, то изделие уходит в брак.

Температура печи колеблется случайным образом вокруг 105 градусов с разбросом 15 градусов. Время обработки колеблется случайным образом вокруг 11 минут с разбросом 2 минуты.

Предусмотреть обработку последовательности 100 изделий друг за другом и счетчики количества годных и бракованных изделий.

Задание 11

Напишите уравнения системы.

Имеется железнодорожный состав из тепловоза и двух вагонов, последовательно к нему подцепленных, с грузоподъемностью 10 и 15 тонн. Вагоны подаются тепловозом последовательно под погрузку зерном из бункера.

Первый вагон с помощью продергивания состава встает на весы, что определяет датчик весов. В него начинает подаваться переменным потоком зерно из бункера, который открывается, как только вагон встает под погрузку. Команду бункеру (сыпать/не сыпать) на погрузку и ее прекращение дает датчик весов, находящихся под вагоном, в который дополнительно поступает информация о грузоподъемности вагона. Как только вагон полностью загружен, датчик подает сигнал тепловозу, который продергивает состав на один вагон, и процесс повторяется со вторым вагоном. В конце погрузки состава датчик дает сигнал на отправку всего состава и закрытие погрузочного бункера.

Задание 12

Дана технологическая линия (ТЛ), состоящая из типовых узлов обработки (УО). Каждый элемент ТЛ (УО) состоит из входного склада для хранения сырья, ожидающего обработки в этом узле и обрабатывающего органа (станка). Склад характеризуется максимальной емкостью Xm (кг), станок – максимальной производительностью обработки Um (кг/час). Текущее количество сырья на складе – Х (кг). Надо учесть, что часть обработанной продукции (постоянный заданный процент) становится браком, остальная продукция поступает на следующий УО для дальнейшей обработки.

Если на складе по какой-либо причине сырье отсутствует, то станок данного УО останавливается (простой). Если склад переполняется, то станок предыдущего УО останавливается. Количество сырья на входе ТЛ – неограниченно. УО останавливается также, если станок ломается.

УО бывают трех типов: слияние (два предшествующих потока сбрасывают сырье для УО на его входной склад), сборка (два предшествующих потока должны поставлять два потока в оговоренной пропорции А:В для получения одного сборочного изделия на текущем УО), разделение (УО разделяет обработанный станком поток на два в оговоренной пропорции C:D, подавая эти потоки на две разные ветки ТЛ).

Задайтесь видом ТЛ. Напишите уравнения системы.

Постройте конструктор из УО для набора компьютерной модели любой ТЛ. Установите регуляторы на переменные производительности обработки станков ТЛ. Промоделируйте систему в автоматическом режиме. Приведите графики несколько вариантов поведения ТЛ.