|
Практика 3. Регрессионная модель динамической системы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| X | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Y | 0 | 1.9 | 5.1 | 6.8 | 6.5 | 5.3 | 4.4 | 4.3 | 4.8 | 5.2 | 5.3 |
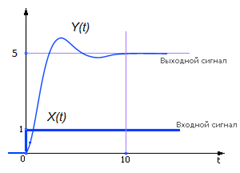
Нарисуйте графики X(t) и Y(t) в осях координат XOt и YOt, то есть установите на график точки из таблицы экспериментов и соедините их плавной кривой линией. Оцените поведение системы, предложите вид гипотезы, описывающей данную систему, – уравнение.
|
|
| Рисунок – График одного из вариантов поведения системы второго порядка |
По графику видно, что система обладает колебательными свойствами. Это означает, что ее порядок не может быть меньше 2. Простейшей гипотезой о динамической системе второго порядка является уравнение:
A*Y’’+R*Y’+M*Y = K*X, где A, R, M, K – коэффициенты, значения которых надо определить, линейного дифференциального уравнения при нулевых начальных условиях, а Y(t) задана таблично, X(t)=1.
Переформулируйте уравнение, избавившись от необходимости определения одного коэффициента. (Один коэффициент такого уравнения произвольно можно задать равным 1, от этого суть уравнения не изменится).
Проинтегрируйте дважды выбранное дифференциальное уравнение, превратив его в интегральное уравнение второго порядка.
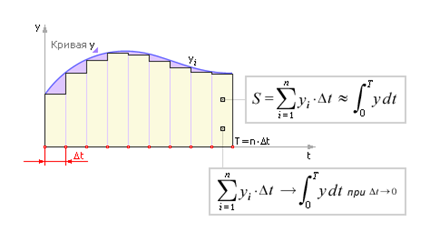
Замените интегралы их дискретными аналогами - суммами. ∫xdt ≈ ∑xi*Δt. Не забудьте ввести индекс i для переменных из-за замены аналоговой величины x(t) на дискретную xi. На рисунке показана простейшая схема дискретизации аналогового сигнала методом прямоугольников.
|
|
| Рисунок – Замена непрерывной кривой ее дискретным аналогом методом прямоугольников |
Учтите, что при двойном интегрировании вместо ∫∫x(t) с интегралами от 0 до промежуточного τ у внутреннего интеграла и от 0 до текущего момента времени t у внешнего интеграла, где τ<t, в ряде случаев появляется двойная сумма ∑(∑(хj*Δt))*Δt с индексами j (у внутренней суммы от 0 до i) и i (у внешней суммы от 0 до m).
Из таблицы видно, что расстояние между двумя временными отсчетами Δt=1 (частный случай).
Следует также учесть, что при формировании выражения расчета суммарной ошибки F будет необходимо третий раз просуммировать все N значений заданных нам экспериментальных точек по индексу m от 0 до N, где N=10.
Схема расчета двойных сумм показана на рисунке:
|
Далее следует минимизировать функцию F от трех переменных, приравняв производные от F по этим коэффициентам нулю. Упростите уравнения, приведя подобные и записав систему в традиционном матричном виде. Решите систему линейных алгебраических уравнений с тремя неизвестными коэффициентами методом Крамера. Определив значения коэффициентов, установите их в изначальное дифференциальное уравнение. Запишите для него начальные условия и x(t)=1.
Решите полученное линейное дифференциальное уравнение второго порядка с известными коэффициентами и начальными условиями любым известным вам методом из курса высшей математики, например, операторным методом.
Найдите решение уравнения, найдя функцию Y(t)=f(Х(t)), то есть формулу Y(t)=… в явном виде.
Начертите расчетный график полученной функции Y(t) на тех же осях, где изображена экспериментальная кривая, рассчитав значения Y в точках t=0,1,2, … ,10.
Найдите суммарную ошибку F=∑E2, где сумма ошибок берется по 10 точкам для t от 1 до 10 шагом 1.
Найдите относительную ошибку σ, приведенную на одну точку.
Удобно вторую часть расчетной (расчет ошибок, проверка) таблицы иметь в следующем виде.
Таблица - Расчет параметров гипотезы методом наименьших квадратов
| Экспериментальные данные | Расчетные данные | Расхождение теории и эксперимента | Проверка, ответ | ||||
| № точки | Xi | Yi | YTi | Ei=YTi -Yi | Ei2 | YTi- сигма | YTi+ сигма |
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | |||||||
| 7 | |||||||
| 8 | |||||||
| 9 | |||||||
| 10 | |||||||
| N=10 | Cумма Xi | Cумма Yi | F – сумма Ei2 | L точек попало в интервал [YTi – сигма, YTi + сигма] | |||
| A=…, R=…., M=…. | Сигма=√(F/n) | Гипотезу принимаем или не принимаем, так как … | |||||
Постройте параллельно расчетной кривой YT еще две кривые на расстоянии ±δ от нее. Получится коридор точности. Определите, сколько экспериментальных точек попадает в коридор точности ±δ. Определите, сколько точек попадает в коридор точности удвоенной ширины ±2δ.
Если попавших в коридор точности точек не менее 68% и в удвоенный коридор точности не менее 95%, то гипотеза принимается.
Сделайте и запишите вывод.
Подсказка. Некоторые контрольные числа для самопроверки: -5191.7, -39979.9, -47091.3, 4.69, -0.13, 0.62, -1.99, 26.08, 1.70.
Примечание. Метод аппроксимации дифференциальных уравнений интегрированием с последующей дискретизацией можно упростить, если замену осуществлять методом Рудольфа Калмана (замена производных конечными разностями).
| О руководителе курса «Моделирование систем» | Лекция 02. Линейные регрессионные модели | ||||||||||||||||
|
|||||||||||||||||