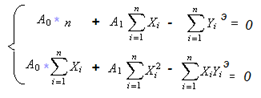|
Практика 2. Регрессионные модели
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
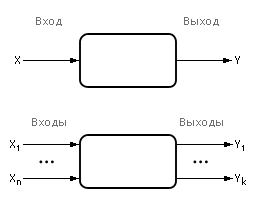
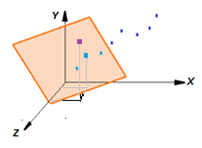
| Рисунок - Одномерная и множественная модели черного ящика |
Задание 1. Одномерная линейная статическая регрессионная модель
Постройте две взаимно перпендикулярные оси X и Y, оцифруйте и подпишите их. Например, X – количество использованной предприятием электроэнергии, Y – количество выпущенной продукции.
Поставьте на осях 10 точек, стараясь попасть в узлы сетки (так легче считать). N=10. Реально координаты таких точек определяют экспериментом, а точки называются экспериментальными.
Например:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| X | 1 | 3 | 3 | 4 | 6 | 7 | 8 | 9 | 12 | 15 |
| Y | 0 | 2 | 4 | 4 | 5 | 6 | 9 | 11 | 10 | 18 |
При установке точек исключите две крайности – не устанавливайте точки ровно по одной линии и не распределяйте точки равномерно по всему полю. В первом случае поиск закономерности становится тривиальным, во втором – закономерность вовсе отсутствует.
|
|
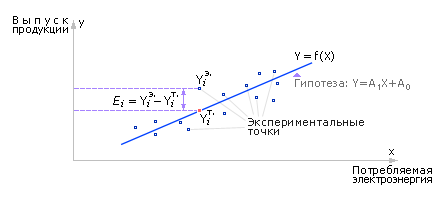
| Рисунок – График теоретической зависимости (гипотезы) и экспериментально наблюдаемые точки. Показаны ошибки (промахи) экспериментальных точек относительно теоретической линии |
На черновике проведите несколько прямых линий, стараясь расположить их так, чтобы прямая проходила как можно ближе сразу ко всем точкам. Такая линия называется теоретической. Разумеется, пройти точно через все точки, имеющие разброс, прямая не может.
Как точно найти наилучшую прямую?
Для этого надо подобрать наилучшие параметры (коэффициенты) прямой линии A0 и А1. При изменении значений А0 и А1 прямая линия перемещается и вращается. Среди всех возможных ее положений надо найти такое, у которого точки теоретической прямой для заданных Х располагаются ближе всего к экспериментальным точкам с такими же значениями Х. На математическом языке это означает, что суммарная ошибка F всех точек должна быть минимальной.
F -> min(A0,A1)
Суммарная ошибка F – сумма ошибок Ei каждой из точек. Ошибка точки – это разность между значением Y экспериментальной точки и значением Y точки на искомой теоретической прямой с той же координатой Х, что и соответствующая экспериментальная точка.
F = ∑(Yтi-Yэi)2 -> min(A0,A1) – сумма для всех i, которые меняются от 1 до N, i – номер точки в экспериментальной таблице. В квадрат выражение под суммой мы возвели для того, чтобы точки выше прямой, имеющие значение (Yтi-Yэi) меньше нуля, не компенсировались точками ниже прямой, имеющим значения (Yтi-Yэi) больше нуля. В этом случае ошибка F была бы равна нулю (или примерно равна 0), хотя точки и имели бы значительные разброс. Чтобы исключить ситуацию, когда точки имеют ошибку, но она математически не обнаруживается, берут ошибки одного знака, возводя их значения в квадрат.
Так так Yт=A0+A1*X, то F=∑(A0+A1*Xi -Yэi)2 -> min(A0,A1)
Рядом с символом «min» обязательно надо указывать, за счет чего вы собираетесь достигать такого минимума, каким ресурсом вы свободно располагаете, меняя его значение. В нашем случае изменение F происходит за счет параметров предполагаемой функции A0 и A1. Разумеется, в техническом устройстве должна быть возможность менять такие величины по своему усмотрению.
Для начала мы предположили, что функция линейна: Yт=A0+A1*X – гипотеза о виде теоретической функции. Мы выбрали наиболее простую функцию, ориентируясь на вид ее графика. Если в конце концов окажется, что такая гипотеза не удовлетворит нас после ее проверки, то надо будет гипотезу изменить, а функцию усложнить. Такой подход основывается на принципе, который называется «бритва Оккама»: «Не вводи сущностей без надобности». В нашем случае прямой линии (линейной функции) сущностями являются A0 и А1 – две степени свободы, благодаря изменению значений которых прямая может подбираться ближе к экспериментальным точкам, оставаясь прямой.
Плавно меняя значения А0 и А1, плавно будет меняться расстояние F от экспериментальных точек до теоретической прямой. Таким образом, F является непрерывной функцией аргументов A0, A1: F(A0, A1). А, значит, у функции F можно найти экстремум. По практическим соображениям максимума функция F не имеет, а минимум у нее есть обязательно и он единственный.
Функция F – это непрерывная гладкая функция двух аргументов, поэтому, чтобы найти ее минимум, необходимо найти производную по каждой из ее переменных А0 и А1. А так как в точке экстремума F ее производные равны нулю (математическое свойство производной в точке экстремума), то для того, чтобы найти численные значения параметров А0 и А1, следует выражения производных приравнять нулю.
|
|
| Рисунок – Примерный вид функции ошибки F |
Получится два уравнения с двумя неизвестными А0 и А1, которые можно решить и найти значения А0 и А1. Это и будут те параметры, которые определят наклон и положение искомой прямой Y=f(X), которая будет одновременно ближе сразу ко всем экспериментальным точкам.
Итак, dF/dA0=0 и dF/A1=0.
То есть, используя правило взятия производной от сложной функции, получаем:
dF/dA0 = ∑2*(A0+A1*Xi - Yэi)
dF/A1 = ∑2*(A0+A1*Xi - Yэi)*Xi
или
или
|
для i, меняющихся от 1 до N в знаках сумм.
Имеем систему двух линейных уравнений с двумя неизвестными A0 и A1. Все значения Xi, Yi – известны (смотри график и таблицу).
|
В уравнениях раскрыты скобки и отмечен тот факт, что 2*Z=0 предполагает, что из двух сомножителей 2< >0, а, значит, Z=0.
Для лучшего понимания представьте данные выражения в виде 10 слагаемых, раскройте скобки, перегруппируйте слагаемые, приведите подобные.
В результате запишем систему уравнений в традиционном матричном виде:
|
С помощью метода Крамера найдем формулы для расчета А0 и А1:
|
Подставляя в формулы значения Xi, Yэi для i от 1 до N из экспериментальной таблицы, рассчитаем значения А0 и А1. Рекомендуем для расчета воспользоваться Excel.
| Экспериментальные данные | Расчетные данные | Расхождение теории и эксперимента | Проверка, ответ | ||||||
| № точки | Xi | Yi | Xi2 | Xi*Yi | YTi=A0+A1*Xi | Ei=YTi -Yi | Ei2 | YTi - сигма | YTi + сигма |
| 1 | 2 | 3 | |||||||
| 2 | 3 | 2 | |||||||
| 3 | 4 | 5 | |||||||
| 4 | 2 | 4 | |||||||
| 5 | 3 | 6 | |||||||
| 6 | 6 | 7 | |||||||
| 7 | 7 | 9 | |||||||
| 8 | 8 | 10 | |||||||
| 9 | 9 | 11 | |||||||
| 10 | 10 | 15 | |||||||
| N=10 | S – Cумма Xi S= | P – cумма Yi P= | M – cумма Xi2 | K – cумма Xi*Yi | F – сумма Ei2 | L точек попало в интервал [YTi – сигма, YTi + сигма] | |||
| A0=(P*M-S*K)/(n*M-S*S) A1=(N*K-S*P)/(n*M-S*S) Y = A0+A1*X | Сигма=√(F/n) | Гипотезу Y=A0+A1*X принимаем или не принимаем, так как … | |||||||
Конкретно:
| i | Xi | Yэi | X2i | Xi*Yi |
| 1 | 1 | 0 | 1 | 0 |
| 2 | 3 | 2 | 9 | 6 |
| 3 | 3 | 4 | 9 | 12 |
| 4 | 4 | 4 | 16 | 16 |
| 5 | 6 | 5 | 36 | 30 |
| 6 | 7 | 6 | 49 | 42 |
| 7 | 8 | 9 | 64 | 72 |
| 8 | 9 | 11 | 81 | 99 |
| 9 | 12 | 10 | 144 | 120 |
| 10 | 15 | 18 | 225 | 270 |
| N=10 | ∑Xi=68 | ∑Yi=69 | ∑X2i=634 | ∑XiYi=667 |
| (∑xi)2=4624 |
Итого:
А0=(69*634-68*667)/(10*634-4624)=-1610/1716 = -0.94
A1 = (10*667-68*69)/(10*634-4624) = 1978/1716 = 1.15
Схема компьютерной реализации расчета коэффициентов выглядит следующим образом:
|
|
| Рисунок – Схема технической реализации расчета коэффициентов линейной гипотезы черного ящика с использованием данных об экспериментах |
Дополним таблицу. Зная значения А0=-0.94 и А1=1.15, вычисляем yтi точки на прямой, соответствующие значениям xэi, а также ошибку каждой точки E2i=(yтi-yэi)2 и суммарную ошибку всех точек F.
| i | Xi | Yэi | X2i | Xi*Yi | Yтi=A0+A1*Xi=-0.94+1.15*Xi | Ei=Yтi-Yэi | E2 |
| 1 | 1 | 0 | 1 | 0 | 0.21 | 0.21 | 0.04 |
| 2 | 3 | 2 | 9 | 6 | 2.51 | 0.51 | 0.26 |
| 3 | 3 | 4 | 9 | 12 | 2.51 | -1.49 | 2.22 |
| 4 | 4 | 4 | 16 | 16 | 3.66 | -0.34 | 0.12 |
| 5 | 6 | 5 | 36 | 30 | 5.96 | 0.96 | 0.92 |
| 6 | 7 | 6 | 49 | 42 | 7.11 | 1.11 | 1.23 |
| 7 | 8 | 9 | 64 | 72 | 8.26 | -0.74 | 0.55 |
| 8 | 9 | 11 | 81 | 99 | 9.41 | -1.59 | 2.531 |
| 9 | 12 | 10 | 144 | 120 | 12.86 | 2.86 | 8.18 |
| 10 | 15 | 18 | 225 | 270 | 16.31 | -1.69 | 2.86 |
| N=10 | ∑Xi=68 | ∑Yi=69 | ∑X2i=634 | ∑XiYi=667 | ∑E2i=18.91 | ||
| (∑xi)2=4624 | F = 18.91 |
Примечание. Обратите внимание: точек с E>0 и точек с E<0 примерно равное количество. Это говорит о том, что найденная теоретическая прямая проходит через совокупность экспериментальных точек «по середине».
Вычислим относительную ошибку, приходящуюся на одну точку из N=10, и извлечем квадратный корень (так как ранее возводили ошибку в квадрат F=∑E2):
δ=√(F/(N-p))=1.54,
где p – количество использованных степеней свободы в составе гипотезы (в нашем случае p=2).
Проверим, насколько обоснованно мы приняли гипотезу о том, что искомая функция – линейная (с графиком в виде прямой линии).
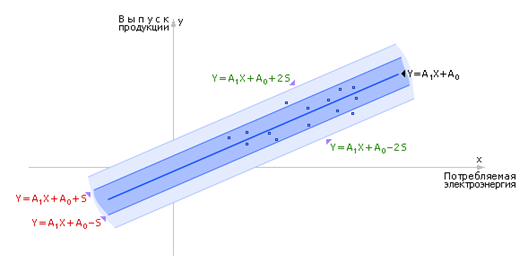
Для этого прочертите в осях XОY найденную Вами прямую Y=A0+A1*X. В моем примере: Y = -0.94+1.15*X. Прямая должна пройти через середину совокупности экспериментальных точек.
Проведите на расстоянии ±δ две прямые, параллельные полученной теоретической прямой (выше и ниже ее на расстоянии δ). Пересчитайте количество точек, попавших в коридор точности [yт-δ≤yэ≤yт+δ].
|
|
| Рисунок – График линейной гипотезы и коридоров точности с экспериментальными точками |
Чтобы принять гипотезу, необходимо, чтобы в коридор точности ±δ попало не менее 68% экспериментальных точек и в коридор [yт-2δ≤yэ≤yт+2δ] попало не менее 95%.
|
|
| Рисунок – Обоснование ширины коридоров точности предположением о нормальном распределении ошибки |
Таким образом, наша гипотеза – не есть полный произвол, как это может показаться сначала. Гипотеза, чтобы ее принять или отвергнуть (и перейти к другой), обязательно в конце расчета проверяется.
Если условия принятия гипотезы не выполняются, то необходимо выдвинуть более сложную гипотезу и провести все ранее описанные шаги с ней заново.
Задание 2. Нелинейная одномерная статическая регрессионная модель
Не важно, принялась Ваша линейная гипотеза или нет, в учебных целях, проведите усложнение (уточнение) Вашей гипотезы и с теми же экспериментальными точками проведите еще раз этот расчет – найдите формулы расчета и значения коэффициентов новой регрессионной модели, проведите проверку гипотезы, сделайте прогноз 2-3 новых точек. Оцените точность новой нелинейной модели по сравнению со старой (линейной моделью). Сделайте вывод – принимается новая гипотеза или нет. Приведите геометрическую иллюстрацию модели.
Теория
На роль более сложных гипотез могут претендовать функции с нелинейным поведением и (или) с бо’льшим числом степеней свободы (количеством коэффициентов). Например, Y=A2*X2+A1*X+A0, Y=A0+A1*sin(A2*X+A3), Y=A0*exp(A1*X)+A2 и т.п..
При выборе функции надо ориентироваться на вид графика функции.
Повышать количество степеней свободы следует постепенно, каждый раз проверяя - выполнится условие принятия гипотезы или нет («Не вводи сущностей без надобности»). В сложных случаях может появиться даже дерево постепенно усложняющихся гипотез.
Примечания.
1. Надо ли для 10 точек применять сразу полином 9 степени? Конечно, полином 9 степени пройдет точно через 10 точек. Хорошо ли это? - Нет. Так как добавление следующей экспериментальной точки приведет к тому, что достигнутая ранее 100%-я точность не будет сохранена. В данном случае достигнутая точность – иллюзия, с которой надо быть осторожнее.
2. Если некоторые точки при одном и том же значении X имеют разные значения Y – вертикально расположенные точки (при одной причине – разные следствия), то это может означать, что мы имеем дело: – с ошибкой измерения. Следует проверить полученные ранее экспериментальные значения точек.
|
|
| Рисунок – Вертикальные точки на графике – одна и та же причина Х1 привела к разным следствиям Y1 и Y2 |
- с дополнительным входным фактором Z, действующим на наш черный ящик. Например, по понедельникам, средам и пятницам при Х=5 черный ящик показывает Y=2, а по вторникам, четвергам и субботам при Х=5 черный ящик на выходе показывает значение Y=4. Можно предположить, что, видимо, по нечетным дням за стеной лаборатории включают электромагнитное поле, которое незаметно для нас влияет на работу черного ящика переменной Z. Одна из гипотез в этом случае может выглядеть так: Y=A0+A1*X+A2*Z. Дополнительный фактор Z вносит свою лепту в результат Y.
В системотехнике это соответствует новому дополнительному элементу, который надо ввести в систему. На входе появляется новый дополнительный вход Z, модель становится множественной. Размерность модели увеличивается. Система статическая.
|
|
| Рисунок – Появление плоскости при введении третьей координаты - при (X1,Z1) функция принимает значение Y1, при (X1,Z2) - значение Y2 |
3. Если в отдельной области множества Х прямая начинает заваливаться (искривляться), отклоняться от своего поведения в других областях, то это означает, что имеет место влияние факторов друг на друга или самих на себя: X*Z, X2, exp(x). Это говорит о том, что в структуре системы появляются дополнительные внутренние связи. Например, та же самая экспоненциальная функция скрывает в себе внутренние связи:
|
Модель становится нелинейной, например, с обратными связями. Система нелинейная статическая.
|
|
| Рисунок – При Х>X1 график функции меняет свою тенденцию |
4. Метод (как наименьших квадратов, так и научный, вообще) может обманывать. Например, точки описывают две зависимости (показано серым цветом), но общий результат дает совсем другую зависимость (показано красным цветом).
|
Научный метод обнаруживает четкую связь (корреляцию) между потреблением маргарина и количеством утонувших в бассейнах. Но есть ли в самом деле такая причинно-следственная связь?
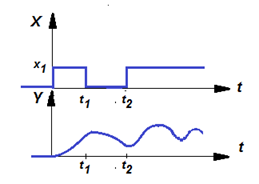
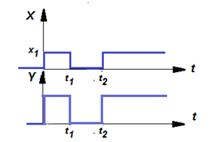
5. Если в момент t1 черный ящик на значение входа Х отвечает значением Y, а в момент t2 на то же значение входа Х отвечает другим значением Y, то черный ящик – динамический. В этом случае система является системой с памятью и описывается формулой, содержащей производные (или интегралы). Выход динамической системы зависит не только от того, каков ее входной сигнал, но и от того, в каком состоянии находилась система в предыдущий момент (от истории поведения системы).
Если значение выходного сигнала системы зависит от нескольких предыдущих состояний от текущего, то говорят, что динамическая система имеет порядок n>1, то есть ее запись содержит производные, включая n-ую степень, где n – порядок старшей производной. Статическая система имеет n=0 и памяти о прошлых своих состояниях не имеет.
|
|
| Рисунок – Динамическая система: на один и тот же сигнал X1 в разное время t1 и t2 (при разных обстоятельствах) характер и значения отклика системы Y(t) разные |
|
|
| Рисунок – Статическая система: на один и тот же сигнал X1 в разное время t1 и t2 значение выходного сигнала Y(t) одно и тоже |
6. Система (связи и элементы) сама перестраивается в зависимости от текущего собственного состояния и принимаемых входных сигналов. Такие системы, борющиеся с окружающей средой, имеющие собственную цель, которую они стремятся постоянно достигать, называются рефлексивными и рассматриваются в дисциплине «Искусственный интеллект».
7. Еще более сложным случаем является присутствие случайного фактора. Точки «пляшут». Эксперимент при одних и тех же условиях может давать разные значения выходного сигнала. Система – стохастическая. Это может свидетельствовать о недостаточном нашем знании о действующих факторах и связях в системе. Неспособность представить себе все элементы и связи такой большой и сложной системы говорит о слабой предсказуемости нами ее поведения. Типичный пример такой системы – человек и его поведение. В этом случае оперируют средними значениями переменных.
8. Иерархические системы также являются достаточно сложным новым случаем.
Случаи 2,3,4,5,6,7 будут рассмотрены далее отдельно.
Кроме указанной проверки могут использоваться дополнительные проверки. Количество проверок ничем не ограничено. Чем больше проверок, тем надежнее подтвержденный ими результат. (Однако следует иметь в виду, что даже при бесконечном количестве проверок нельзя сказать, что результат гарантирован на 100%).
Прогноз. Зная полученную формулу зависимости Y=A0+A1*X, например, Y = - 0.94+1.15*X, можно предсказывать положение новых точек, отсутствующих в экспериментальной таблице. Например, подстановкой X=10 в полученную формулу получаем значение Y=10.56 и т.д.. Модель (формула, уравнение) демонстрирует прогнозирующую роль в отличие от таблицы данных, выполняя познавательную функцию.
Вывод
Собственно, ради прогноза, то есть получения новой информации, и осуществляют регрессионный анализ. Кроме этого, получение информации о составе и структуре «черного» ящика (он становится «белым») дает нам знания о том, как он устроен и как его построить. Метод, которым мы воспользовались, называется метод наименьших квадратов. Процедура – обобщение.
Примечание
К результатам регрессионного анализа следует относиться с осторожностью. Следует правильно интерпретировать его данные.
Например, регрессионная модель формально может показать, что количество маргарина X, потребляемого на душу населения в Пермском крае, коррелирует с интенсивностью разводов в Перми Y или с количеством утонувших в бассейнах. Хотя очевидно, что прямой такой связи реально не существует. Со временем растет и та, и другая величина, но причинно-следственной связи между этими явлениями нет.
Еще пример. В нашем случае при X=0 (отсутствие потребления предприятием электроэнергии) следует ожидать отсутствие выпуска предприятием продукции. Однако модель предсказывает Y=-0.94, что означает выпуск какого-то отрицательного количества продукции.
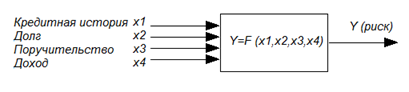
Задание 3 (вариант 1). Многомерная линейная статическая регрессионная модель
Описание задачи
Эксперт – банковский служащий, решающий вопрос о выдаче кредита клиентам. Наблюдение за экспертом показало, что в результате 14 экспериментов эксперт спрашивал у клиентов и принимал во внимание «Кредитную историю», «Наличие долга у клиента», «Наличие поручителей», «Доход клиента».
При этом Кредитная история могла быть плохой, неизвестной, хорошей,
Долг – высокий или низкий,
Поручительство – нет или адекватное,
Доход – 0-15 тысяч рублей, 15-35 тысяч рублей, более 35 тысяч рублей.
Решением эксперта являлась оценка риска невозврата кредита, которую эксперт оценивал как высокую, среднюю, низкую .
То есть обозначим:
Y – риск невозврата кредита (высокий В, средний С, низкий Н),
x1 – кредитная история (плохая П, неизвестная Н, хорошая Х),
x2 – долг (высокий В, низкий Н),
x3 – поручительство(нет Н, адекватное А),
x4 – доход (0-15 тысяч рублей М, 15-35 тысяч рублей С, более 35 тысяч рублей В),
Y, x1, x2, x3, x4 – это атрибуты базы данных, переменные закона, признаки.
Значения признаков, числа – это свойства.
На технических схемах это выглядит так.
|
|
| Рисунок – Инженерная схема, отражающая зависимость риска Y от действующих на него причин (x1-кредитная история, x2- долг, x3-поручительство, x4-доход) |
Ищем функцию Y=F(x1,x2,x3,x4) или в наших обозначениях Р=F(К, Дг, П, Дд).
Из наблюдений за экспертом и его общением с клиентами удалось заполнить следующую экспериментальную таблицу фактов. Всего было зафиксировано 14 случаев (14 клиентов, 14 записей базы данных).
Таблица – Экспериментальные данные
| Эксперимент (пример решения) | Риск (Р) | Кредитная история (К) | Долг (Дг) | Поручительство (П) | Доход (Дд) |
| 1 | В | П | В | Н | 0-15 |
| 2 | В | Н | В | Н | 15-35 |
| 3 | С | Н | Н | Н | 15-35 |
| 4 | В | Н | Н | Н | 0-15 |
| 5 | Н | Н | Н | Н | >35 |
| 6 | Н | Н | В | А | >35 |
| 7 | В | П | Н | Н | 0-15 |
| 8 | С | П | Н | А | >35 |
| 9 | Н | Х | Н | Н | >35 |
| 10 | Н | Х | В | А | >35 |
| 11 | В | Х | В | Н | 0-15 |
| 12 | С | Х | В | Н | 15-35 |
| 13 | Н | Х | В | Н | >35 |
| 14 | В | П | В | Н | 15-35 |
В столбце «Риск» базы данных отмечены решения, сделанные на практике экспертом. В столбце «Эксперимент. Пример» - конкретный случай, номер записи базы данных.
Перед применением регрессионного анализа перекодируем содержание таблицы числами в непрерывной области.
Кредитная история – {0,1,2}={П,Н,Х}
Долг – {0,1}={В,Н}
Поручители – {0,1}={Н,А}
Доход – {0,1,2}={0-15,15-35,>35}
Риск – {0,1,2}={Н,С,В}
Рассмотрите датасет отдела кредитования в банке. Составьте регрессионную модель. Нарисуйте геометрическую интерпретацию ответа.
Задание 3 (вариант 2)
Введите в рассмотрение новую дополнительную переменную X2, оставив для переменной X индекс X1. Для этого в экспериментальной таблице предусмотрите дополнительный столбец Х2. Выдвиньте гипотезу о виде зависимости Y=f(X1, X2) и найдите ее коэффициенты методом наименьших квадратов.
Рекомендуется к имеющимся точкам, например, Y=f(5)=10, добавить еще точки, например, Y=f(5)=12. С точки зрения физики это соответствует появлению двух следствий Y=10 и Y=12 при одной и той же причине Х1=5. Естественно предположить при этом существование скрытой переменной Х2, влияющей на Y также, как и X1. Например, при Х2=0 имеем (X1,Y)=(5,10). При X2=1 имеем (X1,Y)=(5,12).
Примечание: все значения чисел здесь примерные. Задаваться надо своими значениями. Рисунок - точки Y=f(X1,X2) - привести в трехмерных координатах.
Примечание: переменные X в расчетных формулах теперь имеют двойной индекс. Первый индекс – номер переменной. Второй индекс – номер экспериментальной точки.
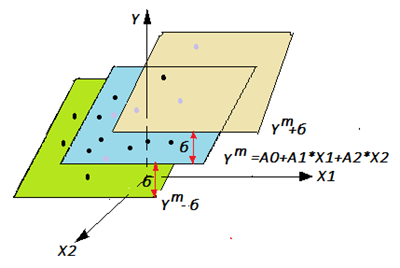
Воспользуйтесь уже выведенной системой уравнений для определения коэффициентов А0, А1, А2 линейной гипотезы: Y=A0+A1*X1+A2*X2.
|
В нашем случае матрица размерностью 3*3 будет соответствовать трем уравнениям с тремя неизвестными: А0, А1, А2.
По таблице с заданными экспериментальными значениями функции вычислите соответствующие коэффициенты системы уравнений и ее свободных членов. Найдите методом Крамера значения неизвестных A0, A1, A2.
Определив значения A0, A1, A2, постройте в системе координат теоретическую плоскость Yт=A0+A1*X1+A2*X2. Плоскость можно построить по трем точкам или по двум прямым (по двум сечениям плоскости) в общем положении. Предположительно плоскость пройдет между экспериментальных точек. Нанесите на рисунок экспериментальные точки по их координатам. При необходимости для наглядности проекционного изображения поверните рисунок относительно осей координат. Заштрихуйте плоскость, по-разному пометьте на рисунке точки, находящиеся выше и ниже теоретической плоскости.
Рассчитайте ошибку гипотезы ±δ. Проведите коридор точности (еще две плоскости, параллельные построенной теоретической плоскости, на расстоянии ±δ от нее, то есть Yт+δ и Yт-δ) и определите количество и процент точек, попавших в слой Yт±δ.
Легче определить эти точки по таблице численно, отметив, – какие точки лежат между двумя крайними плоскостями, а какие – нет.
Отметьте эти точки на рисунке. Сделайте письменно вывод о принятии (или отбрасывании) выдвинутой гипотезы.
|
Важное замечание.
Дополнительные переменные X1, X2, X3, X4, … в состав гипотезы вводят последовательно, проверяя на значимость каждой для результата.
Для определения первой переменной исследуют все входные переменные на корреляцию с выходной переменной.
Линейный коэффициент корреляции указывает, есть ли между двумя переменными X и Y линейная зависимость и какой силы. Вычисляется по следующей формуле:
mx, my, mxy — математическое ожидание x, y, xy:
Дисперсия σx2 и σy2 показывает, насколько разбросаны точки от средней величины:
Отбирают для ввода в формулу переменную X с самым большим по модулю значением KR. После определения коэффициента при введенной переменной проверяют значимость коэффициента при ней. Он должен быть больше нормативно заданного.
Дальнейшие дополнительные переменные вводят последовательно, ориентируясь на коэффициент корреляции каждой из них с выходной переменной Y – от больших значений к меньшим. Каждый раз после определения соответствующего коэффициента, с которым вводится переменная в гипотезу, необходимо проверить значимость этой переменной для гипотезы.
Если ошибка гипотезы F после ввода в нее очередной переменной становится меньше заданного значения (например, 5), то введение новой переменной можно считать нецелесообразным.
Ошибка считается по формуле:
Er=∑(Yiт-my) для i=1,n
Em=∑(Yi-Yiт) для i=1,n
F=1 - Er*(n-k-2)/Em
k – счетчик новых дополнительных переменных к первой.
При введении новой дополнительной переменной коэффициенты при всех ранее введенных переменных меняют свои значения и должны быть пересчитаны.
Второе важное примечание.
«Усложнение гипотезы с точки зрения специалиста по системам»
Если в гипотезу Вы вводите дополнительную входную переменную, то это соответствует появлению новой сущности (например, X2). Сущность – это элемент будущей системы, новое понятие, физическая (или логическая) величина. Сущность выражается чаще всего именем существительным (влажность, температура, … ) и влияет на состав системы. При этом будущее устройство увеличивается на один и более элементов.
Сущности находятся во внешнем мире.
Если в гипотезу Вы вводите дополнительную нелинейность (второй степени, третьей и т.д.), то это соответствует появлению внутри черного ящика (проектируемого устройства) новых связей. Связь – это действие, операция над сущностями (например, X2=X*X – умножить), соединяющая их, устанавливающая их взаимовлияние. Связь выражается чаще всего глаголом (сложить, вычесть, умножить, …) и влияет на структуру системы. Ваше будущее устройство и его поведение усложняется внутри за счет увеличения связей между элементами.
Связи (действия) находятся внутри устройства и составляют его суть. Построить устройство – это значит провести связи между физическими (логическими) элементами.
Система – это элементы и связи.
В матрице множественной линейной регрессионной модели дополнительные элементы влияют на размерность матрицы, а связи между элементами влияют на коэффициенты матрицы (все со всеми). Значения ячеек матрицы – силы связей между переменными. Там, где в матрице стоят нулевые (или малые) значения, связи между соответствующими переменными (сущностями) отсутствуют. Чем больше значение соответствующей ячейки матрицы, тем сильнее связь между этими элементами. Индексы ячейки матрицы – это номера (имена, идентификаторы) связываемых элементов.
Степень взаимосвязи между переменными, сила связи называется корреляцией.
Таким образом, вводя нелинейности и дополнительные входы, Вы усложняете ящик за счет элементов и связей. И то, и другое уточняет гипотезу о черном ящике. Что важнее – определяет исследователь, сравнивая точность различных гипотез.
В общем смысле можно сказать, что хорошие устройства - те, которые имеют больше элементов и меньше связей. Если количество связей равно количеству элементов, то это идеальная линейная структура.
| О руководителе курса «Моделирование систем» | Лекция 02. Линейные регрессионные модели | ||||||||||||||||
|
|||||||||||||||||