|
Практика 1. Формула Ньютона
|
|
|
| Рисунок - Задача о разрезании фигуры на заданное число кусков |
Из рисунка видно, что при 0 разрезах образуется 1 кусок, при 1 разрезе образуется 2 куска, при двух — 4, при трёх — 7, при четырёх — 11. Можете ли вы сейчас сказать наперёд, сколько потребуется разрезов для образования, например, 821 куска? По-моему, нет! Почему вы затрудняетесь? — Вам неизвестна закономерность K = f(P), где K — количество кусков, P — количество разрезов. Как обнаружить закономерность?
Составим таблицу, связывающую известные нам числа кусков и разрезов.
Таблица 1.2. Таблица соответствия разрезов и получающихся фрагментов фигуры
| Разрезы | 0 | 1 | 2 | 3 | 4 | ... |
| Куски | 1 | 2 | 4 | 7 | 11 | ... |
Пока закономерность не ясна. Поэтому рассмотрим разности между отдельными экспериментами, посмотрим, чем отличается результат одного эксперимента от другого. Поняв разницу, мы найдём способ перехода от одного результата к другому, то есть закон, связывающий K и P.
Таблица 1.3. Таблица соответствия разрезов и получающихся фрагментов фигуры
| Разрезы | 0 | 1 | 2 | 3 | 4 | ... | |
| Куски | 1 | 2 | 4 | 7 | 11 | ... | |
| Первые разности | – | 1 = 2 – 1 | 2 = 4 – 2 | 3 = 7 – 4 | 4 = 11 – 7 | ... | ... |
Уже кое-какая закономерность проявилась, не правда ли?
Вычислим вторые разности.
Таблица 1.4. Таблица соответствия разрезов и получающихся фрагментов фигуры
| Разрезы | 0 | 1 | 2 | 3 | 4 | ... | |
| Куски | 1 | 2 | 4 | 7 | 11 | ... | |
| Первые разности | – | 1 = 2 – 1 | 2 = 4 – 2 | 3 = 7 – 4 | 4 = 11 – 7 | ... | ... |
| Вторые разности | – | 1 = 2 – 1 | 1 = 3 – 2 | 1 = 4 – 3 | ... | ... |
Очевидно, что далее продолжать процедуру вычисления разностей смысла нет.
Теперь все просто. Функция f называется производящей функцией. Если она линейна, то первые разности равны между собой. Если она квадратичная, то вторые разности равны между собой. И так далее.
Функция f есть частный случай формулы Ньютона:
Коэффициенты a, b, c, d, e для нашей квадратичной функции f находятся в первых ячейках строк экспериментальной таблицы 1.5.
Таблица 1.5. Таблица соответствия разрезов и получающихся фрагментов фигуры
| Разрезы | 0 | 1 | 2 | 3 | 4 | ... | |
| Куски | a = 1 | 2 | 4 | 7 | 11 | ... | |
| Первые разности | – | b = 1 | 2 = 4 – 2 | 3 = 7 – 4 | 4 = 11 – 7 | ... | ... |
| Вторые разности | – | c = 1 | 1 = 3 – 2 | 1 = 4 – 3 | ... | ... |
Итак, закономерность есть, и она такова:
K = a + b • p/ + c • p • (p – 1)/2 = 1 + p + p • (p – 1)/2 = 0.5 • p2 + 0.5 • p + 1.
Теперь, когда закономерность определена, можно решить обратную задачу и ответить на поставленный вопрос: сколько надо выполнить разрезов, чтобы получить 821 кусок? K = 821, K = 0.5 • p2 + 0.5 • p + 1, p = ?
Решаем квадратное уравнение 821 = 0.5 • p2 + 0.5 • p + 1, находим корни: p = 40.
Составленная по ряду данных модель дала возможность находить ответы на любые вопросы, связанные с ней. Произошло это за счет установления причинно-следственной связи между переменными К и р.
Задание 1
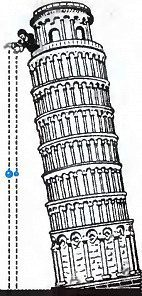
Галилео Галилей пытался найти связь между пространством и временем. Для этого он бросал предметы с башни в городе Пиза. Во время эксперимента он фиксировал путь, пройденный брошенным телом, и время его полета.
|
|
| Рисунок – Опыты Галилея |
Получилась такая экспериментальная таблица
| Время, t | 0 | 1 | 2 | 3 | 4 | 5 |
| Путь, S | 0 | 5 | 20 | 45 | 80 | ... |
Найдите связь между пространством S и временем t для нашей планеты. Обратите внимание на то, что эта формула напрямую связывает пространство и время без посредников.
Примечание. Галилей, наблюдая за качающейся от ветра люстрой в соборе (находится напротив падающей башни в Пизе), открыл еще одну связь между пространством и временем. Первый закон Галилея описывал прямолинейное движение. Второй – вращательное. В природе существует всего два вида движения: прямолинейное и вращательное (колебательное). Все остальные – есть комбинации этих двух движений.
|
|
Задание 2
У куба в зависимости от размерности пространства (N=0,1,2,3,4, …) можно экспериментально определить и указать количество вершин В (нульмерных объектов), ребер Р (одномерных объектов), граней Г (двухмерных объектов), тел Т (трехмерных объектов) и так далее (любых К-мерных объектов).
|
|
| Рисунок – Одномерный, двухмерный, трехмерный, четырехмерный куб (в различных ракурсах) |
Используя таблицу экспериментальных данных, найдите зависимость В(N), Р(N), Г(N), Т(N), …, К(N).
Обобщите полученные формулы в одну алгебраическую конструкцию.
Обратите внимание. Вам придется учесть, что Вы будете иметь дело с производящей формулой 2 порядка сложности.
Важное примечание
1. Неверные данные приводят к неверным законам. Поэтому надо использовать только проверенные данные. Чистота данных важнее их количества.
2. Если данные в отдельной области ведут себя, например, линейно, то это не означает, что они будут вести себя также и в другой области. Например, законы Ньютона верны, пока скорости тел небольшие. Однако, если скорости близки к скорости света в законе существенной становится поправка из общей теории относительности: √(1-v2/c2). А график функции, отражающей закон графически, начинает изгибаться, становится нелинейным. Просто при значениях v<<c этот сомножитель близок к 1, поправка несущественна. И вообще. Не верьте в линейные законы, всякому росту есть предел. Все в итоге нелинейно.
3. Через любое количество конечных точек можно провести бесконечное количество кривых. Экспериментально снять удается только конечное число точек.
Пример.
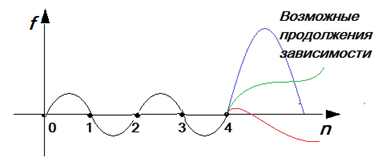
Как вы считаете, увидев последовательность чисел: 0,1,2,3,… какое будет следующе число?
Логика подсказывает, что «4», и напрашивается закон f1=n.
Однако, я могу предложить такой закон: f2=n+n*(n-1)*(n-2)*(n-3)/24.
Можете проверить с калькулятором в руках, этот закон также генерирует последовательность 0,1,2,3,…, но дальнейшее ее продолжение удивляет …5,10,21, … .
Просто f2 сложнее, чем f1, f2 содержит f1 внутри себя. И с увеличением и разнообразием экспериментов выясняется, что мир сложнее, чем мы его себе представляли.
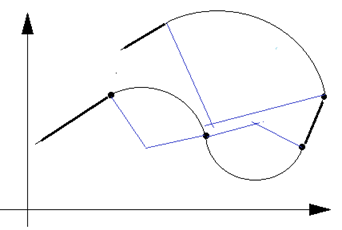
Поставьте несколько точек на график. Проведите различные кривые, которые проходят через эти точки. Таких кривых можно построить бесконечно много.
|
Чтобы определиться с такими ситуациями, в науке используют принцип Оккама: «Не вводи сущностей без надобности». Скажем так, большая часть точности достигается простыми законами, сложные поправки дают меньший вклад в точность ответа. В дальнейшем, при осознанной необходимости добавляют: «от простого к сложному». Сначала испытай простое, если точности не хватает, вводи новые сущности и связи.
4. Получение такого мощного инструмента как формула Ньютона порождает эйфорию в руках исследователя: достаточно просто наблюдать, измерять все вокруг и подставлять в формулу и тебе откроются все законы.
Однако может ли научный метод обманывать?
- Да!
Проведем эксперименты:
1. Водка + вода = алкогольный напиток
2. Джин + вода = алкогольный напиток
3. Коньяк + вода = алкогольный напиток
4. Виски + вода = алкогольный напиток
Из экспериментов следует вывод, что
«вода, добавленная к любой жидкости, это алкоголь».
Однако, мы знаем, что это не так, хотя нами и был применен научный метод. Ошибочный вывод получился из-за того, что количество экспериментов конечно, а вывод касается ВСЕХ (бесконечное число) жидкостей. Просто в выборку не попали мазут, молоко, яблочный сок и т.д.. Разнообразие примеров недостаточно.
Имеет смысл запомнить, что 1 опровергающий теорию контрпример лучше, чем 1000 подтверждающих примеров.
«Лучше принять палку за змею, чем змею за палку». Это то, что называется modus tollens.
| О руководителе курса «Моделирование систем» | Лекция 02. Линейные регрессионные модели | ||||||||||||||||
|
|||||||||||||||||