|
Практическое занятие «Нейроны и нейронные сети»
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
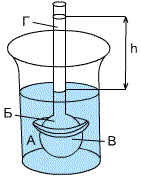
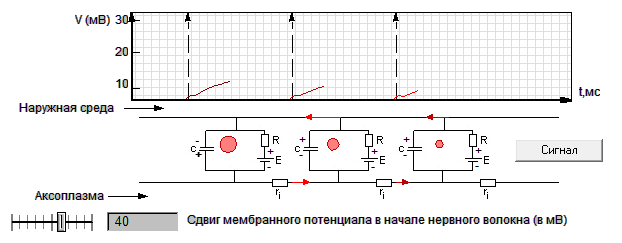
| Рисунок 1.1 – Схема биологического нейрона |
Перечислим основные особенности нейрона, представленные в его модели.
1. В модели Мак-Каллока-Питтса нейрон может находиться в двух состояниях: 0 или 1, то есть 0 – не возбужден, 1 – возбужден. Если нейрон возбужден, то на его выходе поддерживается сигнал 1, если не возбужден – 0.
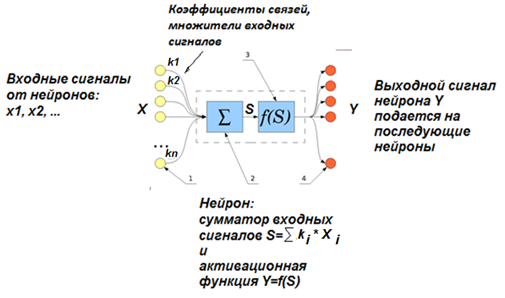
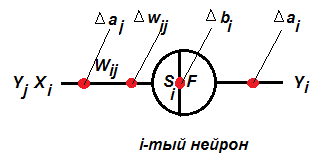
2. Внутри сам нейрон состоит из двух частей: сумматора и активационной функции (рис.1.2).
|
|
| Рисунок 1.2 – Схема искусственного нейрона (1 - предыдущие нейроны сети, 2 – сумматор входных сигналов, 3 – активационная функция, 4 – последующие нейроны сети) |
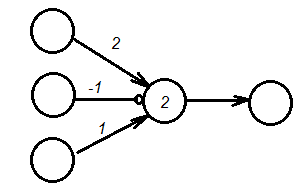
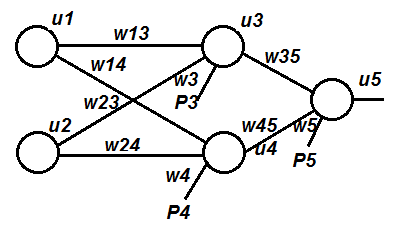
На технических схемах нейрон обозначается кружком (вершиной графа), а связи нейронов – стрелками (связями в графе). На связях ставится вес связи. В кружке указывается значение порога. Нейронная сеть представляется графом.
|
|
| Рисунок 1.3 – Пример нейронной сети из пяти нейронов, связанных между собой |
3. Задача сумматора – получить сигналы X от других нейронов, приходящих к данному нейрону по его входным связям, умножить каждый из них на соответствующее число (k - вес связи) и сложить эти сигналы в общую сумму S по формуле S = Сумма(1, i, ki*xi). Здесь, i – номер входной связи. То есть,
S = k1x1 + k2x2 + … + kixi + … + knxn,
мы имеем дело с линейной функцией S(X). Часто на схемах вес связи обозначают w.
4. Задача активационной функции - нелинейно преобразовать суммарный сигнал S в единственный выходной сигнал нейрона Y:
Y = f(S).
Y является состоянием нейрона и одновременно удерживаемым им его выходным сигналом. Пока состояние Y нейрона не изменится, не изменится его выходной сигнал. Исследователи рассматривают несколько видов функции Y = f(S): ступенчатая, линейчатая (max(0, x) или ReLu), смешанная, сигмоидальная, sign (рис. 1.4). Выбор активационной функции влияет на точность расчетов нейронной сети, наиболее «физичная» из них - сигмоидальная.
|
|
| Рисунок 1.4.1 – Виды активационных функций. Активационная функция представляет собой простейшую нелинейность – скачок, единичную функцию. |
Активационной функция называется потому, что она «решает», возбудится ли нейрон от суммы входных сигналов или нет. Нейрон возбудится, если сумма входных сигналов с учетом весов связей S окажется больше или равна h. Если сумма S окажется меньше h, то нейрон молчит, не возбуждается. Величина h называется порогом возбуждения. Если входные сигналы преодолели порог, то на выходе нейрона появляется 1, если не преодолели – то 0.
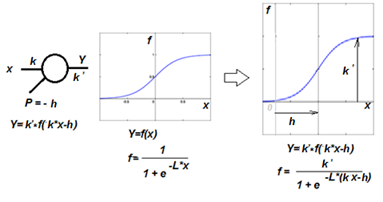
У активационной функции с математической точки зрения, таким образом, есть два параметра – крутизна подъема функции L и сдвиг по оси абсцисс h. Нейрон сдвигает порогом h функцию активации Y = f(x) по оси X и весовым коэффициентом связи масштабирует ее в k’ раз по оси Y:
f = k'/(1 + e(-L*(k*x - h))).
Коэффициент L (и весовой коэффициент k) регулирует крутизну функции.
|
|
| Рисунок 1.4.2 – Математическое описание функции преобразования нейрона Y = f(x) |
Так как у параллельных нейронов сигналы на выходе суммируются, то таким образом можно сложить несколько элементарных функций активации Y = f(X). Кроме того, нейроны, расположенные последовательно, дают возможность чередовать линейную функцию и простейшую (единичную) нелинейную функцию. Эти два механизма объясняют универсальность и высокую гибкость нейронных сетей при моделировании окружающего нас мира, которые могут реализовать по своей сути функцию любой сложности.
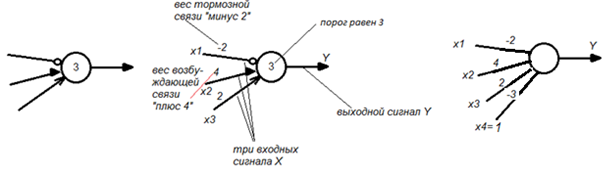
Замечу, порог h в старых схемах часто рисуют в виде числа внутри кружка, изображающего нейрон (рис. 1.5). В новых вариантах изображения сетей порог выносят в виде связи с постоянным значением (–h) и входного сигнала, равного 1 (пример на рисунке), что аналогично в математическом смысле вычитанию значения порога из общей суммы входных сигналов. Последнее время с целью упрощения изображений также перестали рисовать связи, оканчивающиеся стрелками и кружками, заменив их на прямые линии. При этом подразумевается, что сеть передает сигналы слева направо, а знак весового коэффициента указывает на тип связи.
|
|
| Рисунок 1.5 – Изображения нейронов на схемах |
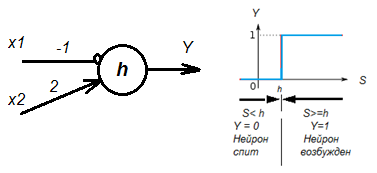
Пример.
На вход нейрона подадим сигналы: X1 = 1, X2 = 1, X3 = 0. Тогда в сумме с учетом входных сигналов и весов связей получится: S = X1*k1 + X2*k2 + X3*k3 + X4*k4 = 1*(-2) + 1*4 + 0*2 + 1*(-3) = -2 + 4 + 0 - 3 = -1. Y = one(-1) = 0. Так как получилось, что S = -1, то есть S < 0, то нейрон «спит», не возбуждается. На выходе нейрона Y = 0.
На вход нейрона подадим сигналы: X1 = 0, X2 = 1, X3 = 1. Тогда в сумме с учетом входных сигналов и весов связей получится: S = X1*k1 + X2*k2 + X3*k3 + X4*k4 = 0*(-2) + 1*4 + 1*2 + 1*(-3) = 0 + 4 + 2 - 3 = 3. Y = one(3) = 1. Так как получилось, что S = 3, то есть S > 0, то нейрон возбужден. На выходе нейрона Y = 1.
Разумеется, могут быть и другие наборы входных данных.
На графиках рисунков 1.4, 1.6 по оси абсцисс отложена переменная S, по оси ординат – переменная Y. Таким образом, активационная функция «передает» сигнал с входа на выход, поэтому ее часто еще называют передаточной функцией. Наиболее часто используют ступенчатую функцию, которая в инженерии называется «функцией Хэвисайда» или единичной функцией Y = one(S) (рис. 1.6).
Порог h может быть любой величиной и настраивается в дальнейшем самой сетью. В примере 1 мы будем сами настраивать пороги. В примере 2 сеть сама настроит пороги, как это реально происходит в «жизни». Порог h сдвигает функцию Y(S(X)) по горизонтальной оси (влево-вправо) на величину его значения.
|
|
| Рисунок 1.6 – График единичной функции Хэвисайда с положительным значением порога h>0 |
Теперь для активационной функции первого типа можно математически записать:
S = k1x1 + k2x2 + … + kixi + … + knxn,
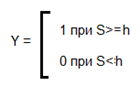
Y = one(S - h) или Y = 1(S - h) или Y:=(S>h).
По-другому, можно записать так:
S = k1x1 + k2x2 + … + kixi + … + knxn,
|
В программировании модель нейрона имеет вид условного оператора:
S = k1x1 + k2x2 + … + kixi + … + knxn,
If (S>=h) then Y:=1 else Y:=0.
Или совсем круто по-программистски (язык СИ++): Y:=1*(S>=h)+0*(S<=h) или сокращенно: Y:=(S>=h).
Или собирая все в одну строку: Y:=((k1*x1 + k2*x2 + k3*x3 - h)>=0).
ВАЖНО! Легко заметить, что h играет роль такого же входного сигнала, как и любой xi. В последних версиях нейросетей h объявляют таким же входным сигналом, как и x (пример 2), а порог ставят равным нулю всегда. Так открывается возможность управлять порогами нейронов сети (то есть логикой сети), унифицируется математическая запись, исчезает необходимость вводить лишнюю сущность (порог).
5. Связи. Далее нейроны объединяют в нейронные сети путем передачи сигналов с выходов Y каждого из них на определенные входы X других с помощью связей. Связь изображается линией, соединяющей нейроны. Связи бывают возбуждающие (k>0) и тормозные (k<0). Если связи нет, то коэффициент связи между соответствующими нейронами равен 0. Один выходной сигнал Y может транслироваться на любое количество входов X других нейронов. Конкретные конфигурации соединений задают конкретную сеть. Конфигурация всей сети задается схемой или (в компьютере) матрицей коэффициентов k, в которой указаны их значения. Квадратная матрица связей сети при этом имеет размер, совпадающий в количеством нейронов сети, которые последовательно пронумерованы.
Принято изображать сеть, упорядочивая нейроны слоями.
6. Потерь уровня сигнала при его раздаче от одного ко многим не происходит. Переход сигнала от нейрона к нейрону происходит за один такт, то есть имеет задержку «единица». Если удерживать входные сигналы в нейронной сети постоянными, то через некоторое время в сети устанавливается постоянство всех состояний и сигналов. (Здесь имеется в виду сеть без обратных связей).
7. Самые первые нейроны в сети - рецепторы (сенсоры, датчики) - получают информационные сигналы из окружающей среды, передавая их интернейронам. Существуют рецепторы шести типов: механорецепторы, электрорецепторы, хеморецепторы, фоторецепторы, терморецепторы, осморецепторы. На выходе сети находятся выходные нейроны: эффекторы или мотонейроны, они прикрепляются к мышцам и заставляют их сокращаться, выполнять команды нейросети (рис. 1.7-1.8). Если вес возбуждающей (заканчивается стрелкой) связи не указан, то он равен «+1». Если вес тормозящей (заканчивается кружком) связи не указан, то он равен «-1». Если в кружке (обозначение нейрона) не указано число, то оно подразумевается равным 0. Если вес связи не равен по модулю единице, то он должен быть указан числом над изображением связи (прямой линией). Если связь идет из «ниоткуда», то это дополнительная связь, задающая «порог».
|
|
| Рисунок 1.7 – Пример изображения вымышленной нейросети |
|
|
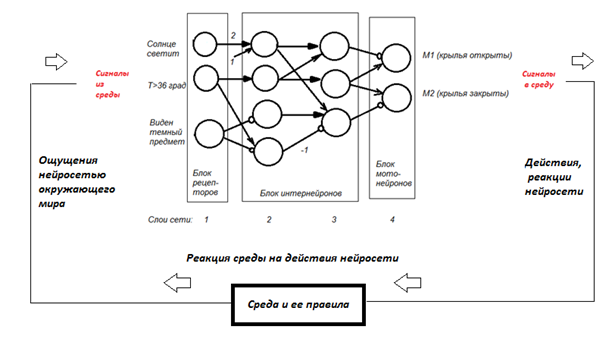
| Рисунок 1.8 – Взаимодействие нейросети и среды |
Исследование свойств нейрона и проектирование нейронной сети
Упражнение 1 «Логические функции, реализуемые нейронами»
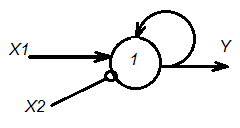
Исследуем свойства нейрона, изображенного на рисунке 1.9.
|
|
| Рисунок 1.9 – Схема нейрона и его активационной функции |
При пороге h = -1 просчитаем реакцию нейрона Y на все возможные варианты входных сигналов X1 и X2 (таблица 1.1).
Таблица 1.1 – Реакции нейрона при h = -1
| X1 | X2 | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Например, рассчитаем выходной сигнал и состояние нейрона Y при входных сигналах X1 = 1, X2 = 1 имеем: S = (-1)*1 + 2*1 = 1, Y = one(S - h) = one(1 - (-1)) = one(2) = 1.
При входных сигналах X1 = 0, X2 = 1 имеем: S = (-1)*0 + 2*1 = 2, Y = one(S - h) = one(2 - (-1)) = one(3) = 1.
При входных сигналах X1 = 1, X2 = 0 имеем: S = (-1)*1 + 2*0 = -1, Y = one(S - h) = one(-1 - (-1)) = one(0) = 1. (Единичная функция возвращает при нулевом аргументе единицу).
При входных сигналах X1 = 0, X2 = 0 имеем: S = (-1)*0 + 2*0 = 0, Y = one(S - h) = one(0 - (-1)) = one(1) = 1.
Видно, что порог h здесь настолько низок, что пропускает все сигналы, проходящие через нейрон, который все время возбужден.
Логическая функция нейрона при h = -1: Y = 1 (нейрон всегда возбужден, независимо от входных сигналов), такой нейрон может служить в нейросетях генератором сигналов.
Еще примеры реакций нейрона при различных значениях величины порога нейрона h.
При пороге h = 0 просчитаем реакцию нейрона на все возможные варианты входных сигналов (таблица 1.2).
Таблица 1.2 – Реакции нейрона при h = 0
| X1 | X2 | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическая функция нейрона при h=0: Y = НЕ (x1) ИЛИ x2. Заметим, что логическая функция изменилась, ИЛИ.
При пороге h = 1 просчитаем реакцию нейрона на все возможные варианты входных сигналов (таблица 1.3).
Таблица 1.3 – Реакции нейрона при h = 1
| X1 | X2 | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическая функция нейрона при h = 1: Y = x2. Заметим, выход Y повторяет один из входов Х2.
При пороге h = 2 просчитаем реакцию нейрона на все возможные варианты входных сигналов (таблица 1.4).
Таблица 1.4 – Реакции нейрона при h = 2
| X1 | X2 | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Логическая функция нейрона при h = 2: Y = НЕ (x1) И x2. Заметим, что функция нейрона сменилась на логику И.
При пороге h = 3 просчитаем реакцию нейрона на все возможные варианты входных сигналов (таблица 1.5).
Таблица 1.5 – Реакции нейрона при h = 3
| X1 | X2 | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Логическая функция нейрона при h = 3: Y = 0. Заметим, что в данном случае выход Y тождественно равен нулю. Нейрон закрыт всегда и никакие сигналы через себя не пропускает.
Анализируя таблицы 1.1-1.5, обратите внимание на то, что в столбце Y появляется все больше нулей, нейрон с увеличением порога h прикрывается, его логика становится жестче. Обобщая примеры, имеем (таблицу 1.6).
Таблица 1.6 – Логические функции нейрона при различных h
| Порог h | Функция Y=one(S-h) | Комментарий |
| <= -1 | Y= 1 | Нейрон возбужден всегда, генератор сигналов |
| 0 | Y=НЕ (x1) ИЛИ x2 | Функция «ИЛИ» |
| 1 | Y= x2 | Нейтральная функция «повторитель» |
| 2 | Y= НЕ (x1) И x2 | Функция «И» |
| >=3 | Y= 0 | Нейрон всегда заперт, тупик, ловушка для сигналов |
Вывод. В зависимости от уровня порога h нейрон может менять логику работы: от мягкой до жесткой, от ИЛИ до И, от «открыто всегда» к «закрыто всегда».
В процессе работы (познания окружающего нас мира) мозг меняет значения порогов, управляя весами связей, меняет логику, то есть правила работы, реакции на мир. Мозг, меняя правила, обучается, находит способ правильно реагировать на окружающую среду. Мозг строит модель. Модель «находится» в связях k и имеет вид уравнений-неравенств. Логика – это связи. Знания – это связи. В биологическом смысле, это означает, что во время обучения у нас вырастают или отмирают, усиливаются или ослабляются аксоны – связи между нейронами, сеть перестраивается. Уравнения задают границы областей, неравенства задают области в многомерном пространстве рецепторов, то есть переменных X.
Задание для самостоятельной работы: нарисуйте три типовых нейрона, каждый из которых реализует логическую схему первый - И, второй - ИЛИ, третий - НЕ. Рассчитайте и запишите таблицу истинности для каждого типа нейрона. Проверьте предложенный вариант описания выхода нейрона в десятичных рациональных числах.
Как известно любую логическую статическую сложную схему можно собрать из комбинации логических элементов: И, ИЛИ, НЕ. Данные нейроны могут служить для Вас элементами конструктора при дальнейшем построении сложной нейронной сети.
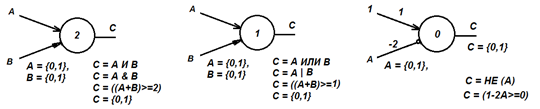
- Нейрон с функцией «И»: С = A&B, C = (A + B >= 2) = (A + B - 2 >= 0) = (-A - B + 2 <= 0)
- Нейрон с функцией «ИЛИ»: C = A|B = (A + B >= 1) = (A + B - 1 >= 0) = (-A - B + 1 <= 0)
- Нейрон с функцией «НЕ»: C = ¬A = (1 - 2A >= 0) = (2A - 1 <= 0)
|
- Любая логическая функция – это комбинация функций И-ИЛИ-НЕ, соединенных последовательно или/и параллельно.
- Любая логическая функция может быть представлена алгебраическим неравенством (равенством).
- Любая алгебраическая система равенств (неравенств) может быть изображена геометрически как некоторое тело в пространстве переменных (рецепторов).
- Любая база статических данных может быть представлена логической функцией в пространстве атрибутов-рецепторов {0,1}.
- Любая база статических данных может быть представлена в виде нейронной сети.
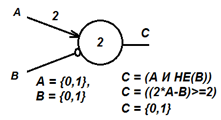
Пример. C = A&НЕ(B)
Заметим, что C = A&НЕ(B) = (2A - B >= 2) = (2A - B - 2 >= 0) = (-2A + B + 2 <= 0) – математическая модель нейрона.
|
|
| Рисунок – Обозначение на инженерных схемах |
Таблица истинности (трассировочная таблица)
| A | B | A&НЕ(B) | 2А-В>=2 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
|
|
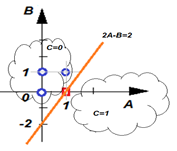
| Рисунок – Геометрическая иллюстрация |
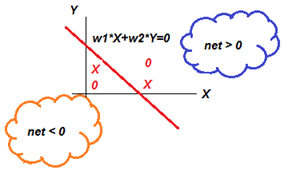
Геометрическая иллюстрация:
- оси координат – рецепторы А и В,
- шкала осей координат - значения рецепторов 0 и 1,
- уравнение нейрона в виде разделяющего правила - прямой линии 2А-В=2,
- две полуплоскости С=1 (нейрон возбужден, правило выполнено) и С=0 (нейрон спит, правило не выполнено),
- точки с координатами из строк таблицы истинности (нейрон спит С=0, нейрон возбужден С=1).
Один нейрон – одна прямая линия, делящая пространство рецепторов на две области (две полуплоскости).
Упражнение 2 «Собака»
Спроектировать нейронную сеть, реализующую задачу.
Задача. Если хозяина нет на кухне, то собака ест мясо как со стола, так и из миски. Если хозяин находится на кухне, то собака не ест мясо со стола, но ест из миски. Если мяса нет, то собака мясо не ест. (Если отдельный сюжет в задаче не оговорен, то принимается любой логичный).
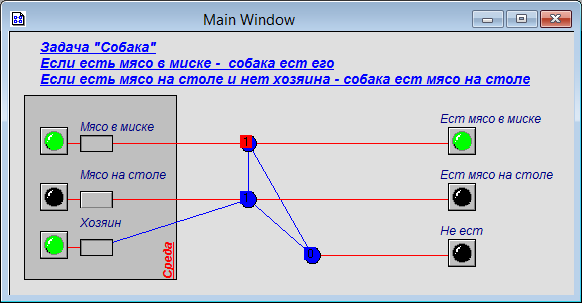
На рисунке 1.10 показан один из вариантов решения задачи в одной из нотаций схем – нейросеть, реагирующая на мясо и хозяина.
|
|
| Рисунок 1.10 – Нейросеть «Собака» |
Покажем еще варианты решения задачи (с использованием среды моделирования Stratum) – рис. 1.11-1.13.
|
|
| Рисунок 1.11 – Реакция сети «Собака» при входных сигналах «мясо на столе»=1, «хозяин»=1 - «не ест»=1 |
|
|
| Рисунок 1.12 – Реакция сети «Собака» при входных сигналах «мясо на столе»=1, «хозяин»=0 - «ест со стола»=1 |
|
|
| Рисунок 1.13. – Реакция сети «Собака» при входных сигналах «мясо в миске»=1, «хозяин»=0 – «ест из миски»=1 |
Пороги указаны в кружках нейронов на схеме. Когда нейрон возбужден и его Y = 1, нейрон на схеме становится красным. Когда нейрон спокоен и его Y = 0, нейрон на схеме становится синим. Наличие входного сигнала на рецепторе (эффекторе) обозначено зеленым цветом. Приведем общую таблицу реакций сети «Собака» (табл. 1.7).
| Рецепторы | Эффекторы | ||||
| Мясо в миске | Мясо на столе | Хозяин на кухне | Ест из миски | Ест со стола | Мясо не ест |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
Математическая модель нейрона: Ест = (2*Мясо - Хозяин + Миска >= 2).
Примечание: любую нейронную сеть, выполняющую заданную функцию, можно собрать бесконечным числом вариантов.
Упражнение 3 «Таракан»
Спроектировать нейронную сеть, реализующую задачу.
Задача. Если есть встречный поток воздуха и ноги касаются земли, то таракан включает микропрограмму «бег». Если есть встречный поток воздуха и ноги не касаются земли, то таракан расправляет крылья и планирует. Если нет встречного потока воздуха, то таракан находится в покое.
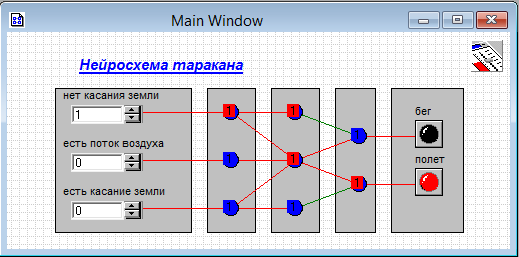
На рисунке 1.14 показан один из вариантов решения задачи в одной из нотаций схем – нейросеть, реагирующая на потоки воздуха и касание земли.
|
|
| Рисунок 1.14 – Нейросеть «Таракан» в одной из нотаций (стрелки не указаны, а подразумеваются с k=1) |
Другое решение приведено на рисунках 1.15-1.17.
|
|
| Рисунок 1.15 – Реакция сети «Таракан» при входных сигналах «нет касания»=1 – «полет»=1 |
|
|
| Рисунок 1.16 – Реакция сети «Таракан» при входных сигналах «есть поток»=1, «есть касание»=1 – «бег»=1 |
|
|
| Рисунок 1.17 – Реакция сети «Таракан» при входных сигналах «нет касания»=1, «есть поток»=1 – «полет»=1 |
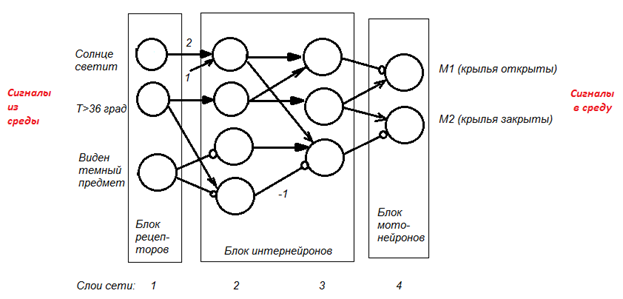
Упражнение 4 (для самостоятельной работы) «Бабочка»
Спроектировать нейронную сеть, реализующую задачу.
Задача. Если солнце есть и температура более 36 градусов, то бабочка складывает крылья, спасаясь от ожога. Если солнце есть и температура T<=36 град., то бабочка раскрывает крылья (греется). Если солнца нет, то крылья сложены (ловить нечего, а тепло не стоит расходовать).
Нарисовать сеть. Обозначить рецепторы. Подписать пороги и весовые коэффициенты связей. Структурировать рисунок сети по слоям.
Оттестируйте построенную схему нейросети. Приведите таблицу истинности.
Запишите формулы нейронов с учетом их связей, то есть модель нейросети. Постройте геометрическую иллюстрацию по модели в осях координат «рецепторы». Подпишите на графике точки, прямые линии, области.
ВАЖНО! Вариантов решения одной и той же задачи множество. Такова природа биологических объектов. Решения отличаются друг от друга разнообразием реакций, надежностью работы схемы по отношению к ошибочному срабатыванию рецепторов, устойчивостью работы сети при случайном обрыве связей.
Продумайте, что произойдет, если у бабочки не будет работать один из рецепторов (ошибка 1-го рода).
Продумайте, что произойдет, если у бабочки один (неизвестно какой) из рецепторов начнет «глючить», то есть вместо 0 выдавать 1 и наоборот (ошибка 2-го рода).
Предусмотрите такие ситуации в схеме для надежности ее срабатывания.
Занятие 2. «Статические нейросети»
Упражнение 1 «Сравниватель на ступенчатых нейронах»
На вход нейросети подается два числа X1 и X2. На выходе находится три нейрона.
Постройте нейросеть, которая реагирует одним нейроном, если X1 > X2, или другим, если X1 < X2.
Если X1 = X2, то срабатывает третий нейрон на выходе.
Таблица 2.1 – Формальное задание поведения нейросети
| Рецепторы | Эффекторы | |||
| Х1 | Х2 | У1 | У2 | У3 |
| 2 | 2 | 0 | 0 | 1 |
| 2 | 5 | 0 | 1 | 0 |
| 5 | 2 | 1 | 0 | 0 |
| 5 | 5 | 0 | 0 | 1 |
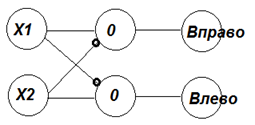
Человек имеет две ушные раковины, размещенные на определенном расстоянии друг от друга. Когда звук раздается слева от человека, то на левую перепонку давит бОльшее звуковое давление, чем на правую. Нейросеть, определит, что Х1>Х2 и даст команду мышцам на разворот головы влево.
Когда звук раздается справа (Х1 < Х2), то формируется команда «поворот вправо». При равенстве звуковых сигналов нейросеть блокирует повороты влево-вправо.
|
|
| Рисунок 2.1 – Движение головы, как реакция на звук |
Простейшая схема управления поворотом головы при детекции звука.
|
Дефектом схемы является «тремор» - подергивание головой в окрестности точки X1 = X2. Улучшим схему. Здесь СА обозначен спонтанно активный нейрон, постоянный генератор сигнала.
|
Упражнение 2 «Сравниватель на линейных нейронах»
Теория.
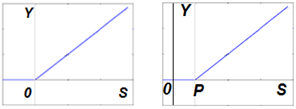
Примем активационную функцию в виде, показанном на рисунке. Если есть ненулевой порог P, то функция сдвигается вправо.
Математическая запись: Y=(X-P)*one(X-P), или Y=max(0, X-P), или Y=(X-P)/2+abs(X-P)/2. Электронщики называют такое устройство диодом. Программист запишет: if (X>P) then Y:=X-P else Y:=0. Традиционно в теории нейросетей такой нейрон называют ReLu (Rectified Linear Unit).
|
Пример. Если на сумматоре нейрон накопил сигнал величиной 5, а порог равен 2, то на выходе нейрона будет сигнал 5 - 2 = 3.
|
На входе нейросети подается два любых неотрицательных числа X1 и X2. На выходе находится один нейрон.
Постройте нейросеть, которая из двух чисел пропускает на выход максимальное из них.
Таблица 2.2 – Формальное задание поведения нейросети
| Рецепторы | Эффектор | |
| Х1 | Х2 | У |
| 3 | 3 | 3 |
| 3 | 7 | 7 |
| 7 | 3 | 7 |
| 7 | 7 | 7 |
Легко заметить, что в арсенале нейросхем появляется эквивалент логического оператора (IF). Напомню, что базисом в алгоритмизации являются: присвоение, условный оператор и циклический оператор.
IF (X1>X2) THEN Y:=X1 ELSE Y:=X2
До этого мы сумели реализовать любые логические функции, имея в арсенале элементы: И, ИЛИ, НЕ.
Упражнение 3 «Детектор цвета»
Человек различает цвета. Примем для простоты 5 цветов: фиолетовый (длина волны - 400 нм), зеленый (500 нм), желтый (550 нм), оранжевый (600 нм), красный (700 нм). Постройте нейросеть, которая на входе получает два сигнала Х1 и Х2 от рецепторов глаза, анализирует их значения и определяет демонстрируемый человеку цвет.
На рисунке показан график чувствительности глазных рецепторов. Рецепторы имеют различную чувствительность к разным цветам. Кроме того, рецепторы образуют сдвиг кривой чувствительности друг относительно друга. Именно это дает им возможность определить конкретный цвет по разнице Х1 и Х2.
|
|
| Рисунок 2.2 – График чувствительности рецепторов Х1 и Х2 к длине волне (цвету) |
Соберите сеть, которая имеет на входе 2 рецептора: Х1 и Х2, а на выходе имеет 5 эффекторов (синий, зеленый, желтый, оранжевый, красный). Преобразуйте комбинацию сигналов Х1 и Х2 в цветовые ощущения цвета.
Добавьте в схему условие «мелкий и движущийся предмет». Например, известно, что лягушка хватает и проглатывает темные, мелкие и движущиеся предметы.
Упражнение 4 «Черепаха Уолтера»
В истории известна реализация кибернетического устройства, собранная из 3 колес, платформы, аккумулятора, фотоэлемента, лампы и бампера с упругим контактом, которая осуществляла:
- движение на свет (приближалась к слабоосвещенным предметам и удалялась от сильно освещенных),
- поисковые движения, исследуя пространство вокруг себя,
- обход препятствий,
- движение к подзарядке по мере истощения заряда аккумулятора,
- узнавание себя в зеркале по отражению в нем собственной лампы.
Соберите схему сети.
Упражнение 5 «Латеральная сеть» (обратное упражнение)
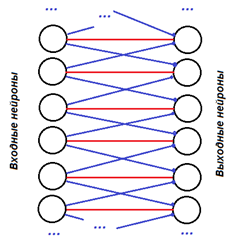
В области лба у человека обнаружены регулярные структуры – нейросети. Определите их предназначение (синим обозначены тормозные связи, красным - возбуждающие) для интеллектуальной деятельности человека.
|
|
| Рисунок 2.3 – Латеральная сеть |
Нарисуйте в тетради латеральную сеть, нарисуйте типичный входной и выходной сигналы на рецепторах и эффекторах, сделайте и запишите в тетради вывод: «что делает данная сеть и для чего она нужна живым организмам».
Занятие 3. «Динамические нейросети»
Динамические сети позволяют реализовать системы с памятью. Естественно, динамическая система обязательно в своем составе будет иметь обратную связь. С точки зрения программирования, это дает возможность реализовать циклы (FOR, WHILE), связанные со счетчиками и другими структурами.
Упражнение 6
Спроектировать нейронную сеть, реализующую задачу.
Задача. Цыпленок с момента рождения клюет все подряд (зерно, мух, ос). Однако, если однажды он клюнет осу, то она его ужалит. И он, почувствовав боль, никогда уже не будет клевать ос, но будет продолжать клевать мух и зерна. У него выработается в процессе опыта отвращение к желтым полосатым объектам.
Это явление называется условным рефлексом. Нейросеть, чтобы вырабатывать у существ условный рефлекс, должна стать динамической. А, как мы знаем, динамические системы – это системы с памятью, с обратной связью. Понятно, что надо уметь запоминать ситуации, приводящие к неприятностям, чтобы избегать их в дальнейшем по появляющимся на горизонте признакам.
На рисунке 3.1 показан нейрон, реализующий запоминание входного сигнала x1. Даже в случае, когда сигнал x1 сначала появляется, а потом исчезает, нейрон помнит о том, что сигнал был. Для этого этот сигнал возвращается по обратной связи на вход нейрона. Чтобы забыть этот факт, достаточно подать сигнал по входу x2, который стирает информацию из памяти (reset). (В сумматоре эти два сигнала гасят друг друга). В инженерии такое устройство называется триггер.
|
|
| Рисунок 3.1 – Сеть, реализующая процесс запоминания, ячейка памяти |
Формально, описать триггер можно функцией: Y:=one(Y + X - R), где Y – выходной сигнал, X – сигнал записи в триггер, R – сигнал сброса состояния триггера. Особенностью записи является то, что она является неявной, уравнением.
Покажем схему условного рефлекса, собранную на двух нейронах (рис. 3.2).
|
|
| Рисунок 3.2 – Сеть, реализующая условный рефлекс |
Первый раз сигнал X пробить нейрон В не может (Y=0) из-за порога h=2, но этот сигнал, тем не менее, проходит на нейрон А и запоминается в нем возбужденным состоянием этого нейрона. На выходе Q теперь постоянно висит сигнал Q=1, помнящий о том, что один раз факт X был.
Когда придет сигнал X второй раз, сеть сработает окончательно (Y станет равной 1), так как двух сигналов X и Q в сумме достаточно, чтобы пробить второй нейрон В. Таким образом сеть умеет считать до двух и запоминать «неприятности», меняя логику на дальнейшие действия. Такие схемы можно сравнить с железнодорожными стрелками, которые закрывают одни пути прохождения сигналов (поездов) и открывают другие по условию.
Сеть, реализующая задачу «Цыпленок. Условный рефлекс» может выглядеть так, как показано на рисунке. В качестве рецепторов принято: «полосатая желтая опасность» и «вкусная и здоровая пища». В качестве эффекторов – «бежать» и «клевать».
|
|
| Рисунок 3.3 – Нейросеть с памятью для реализации условного рефлекса |
Упражнение 7 «Ворона»
Условный рефлекс может быть весьма сложным. Например, было замечено, что вороны умеют считать до 7.
Ворона жила на дереве около замка. На подоконнике окна башни лежал сыр. В дверь башни заходил человек. Ворона, понимая, что в башне есть человек, не рисковала лететь за лакомством. Когда в башню заходили еще три человека, а потом выходило два, ворона все еще не летела за сыром, так как вычисляла, что в башне спрятались два человека. Люди входили и выходили, а ворона считала. Прилетала ворона, чтобы съесть сыр только тогда, когда количество людей в башне было, по ее подсчетам, равно нулю. Сбилась ворона при количестве людей, равном 7.
Спроектируйте сеть, которая умеет считать до 7.
Упражнение 8. Самый известный пример условного рефлекса – собака Павлова.
У собаки выделяется слюна на мясо. Если одновременно с мясом зажигать свет, то через некоторое число повторений этого опыта собака будет выделять слюну на свет, даже если мясо уже будет отсутствовать. У собаки вырабатывается условный рефлекс. Далее, можно повторить опыт со светом и колокольчиком (без мяса). Условный рефлекс вырабатывания слюны перейдет на звук колокольчика. Есть звук – есть слюна, нет звука – нет слюны. Это явление названо Павловым вторичным условным рефлексом. В принципе можно выработать причинно-следственную связь (закон реагирования действием Y на раздражитель X) на любые сигналы (например, на картину Малевича «Черный квадрат»). И только многократный обман, количество которых сеть то же подсчитает, позволит обнулить рефлексы. Так что рефлексы надо время от времени поддерживать, иначе они пропадают.
Спроектируйте сеть «Собака Павлова».
Собака считает количество положительных примеров и количество отрицательных в двух разных счетчиках, сравнивая постоянно их значения между собой. О емкости таких счетчиков в сетях говорят коэффициенты авантюрности и консерватизма, проявляющиеся у отдельных особей (здесь уместно вспомнить автоматы Цетлина).
Упражнение 9.
Реализуйте нейросеть, которая может складывать числа и умножать их (так называемый регистр в вычислительных структурах).
Вывод. Использование логических и динамических систем с памятью открывает пути построения вычислительных систем на их основе.
Занятие 4. Обучение нейронной сети
«Ошибки надо не признавать, их надо смывать кровью».
Занятие. Автоматическое построение нейронных сетей
Упражнения 3.1-3.9 показывают, как вручную можно спроектировать нейросеть. Однако, природа создала сети биологических объектов естественным путем, этот процесс называется «самосборка». По сути, сеть все время ищет равновесное состояние со средой и внутренним своим устройством.
Для этого объект, неверно реагирующий на окружающую среду, наказывается средой (сеть испытывает чувство боли), что приводит к изменению весов связей, сеть перестраивает свою логику. Меняются веса связей (связи появляются и исчезают, усиливаются или ослабляются), меняется структура сети, меняется сама сеть, меняются ее реакции на действия среды. Если объект правильно реагирует на окружающую среду, то он поощряется, сеть не перестраивается.
При получении наказания сеть слегка меняет веса связей и снова вступает во взаимодействие со средой. По мере получения множества наказаний и поощрений сеть медленно флуктуирует в сторону правильной структуры и в конце концов настраивается.
Если среда в последствии изменит уже однажды установившиеся правила игры (случай изменчивости правил у недетерминированной стохастической среды), то сеть почувствует это вновь появившейся болью даже на ситуации, которые ранее поощрялись средой, и снова начнет перестройку своей структуры. Структура задается множеством весов связей нейронов сети.
Биологические объекты всегда учатся, непрерывно реагируя на поступающую информацию. Модель строится непрерывно. Успешность объекта проявляется:
- в способности понять правила (процент адекватных реакций модели на реакции среды в отношении к сумме удачных и неудачных реакций),
- в скорости установления наиболее адекватной модели.
В результате сеть строит свою модель, которая является моделью правил окружающей среды (система математических формул, уравнений, неравенств). Происходит информационный процесс отражения окружающего мира в мозге (нейросети обучаемого).
Как ранее говорилось, искусственный интеллект осуществляет:
- обучение (обобщение) по отдельным данным, строя модель,
- прогноз (экспертизу, предсказание) на построенной модели (с учетом полученного ранее опыта и обобщенного в правила), порождая новые ранее неизвестные данные, упреждая возможные наступающие неприятности, пытаясь избежать их (управление собой и ситуациями).
Моделью сети является набор уравнений-неравенств в многомерном пространстве рецепторов, которые геометрически представляют собой множество областей в этом пространстве, разделенных линиями-границами.
Удивительным является факт угадывания сетью «в какую сторону следует изменять и какие веса», чтобы приблизиться к правильной реакции на действия окружающей среды. Это чутье называется «дельта-правило» и «алгоритм обратного распространения ошибки».
Чтобы построить правильную модель, сеть тратит колоссальные временные ресурсы. Процесс изменения уравнений модели идет очень малым шагом. Оценки показывают, что мозг высокоразвитого существа тратит на мышление бо’льшую часть энергии.
«Мозг, имея массу не более 1,5—2% от массы тела, потребляет 25% всей энергии», «Мозговая деятельность среднестатистических мужчины и женщины ежедневно использует около 450 и 350 ккал в день соответственно, при этом пик работы головного мозга приходится на 5-6-летний возраст, когда этот орган способен использовать до 60% от всей полученной телом энергии».
Огромное время жизни тратится на перестройку модели. Перестройка нейросети мозга происходит во время сна. Сон занимает 50% времени существования биологического объекта. Отсутствие сна лишает его адекватного поведения, разрушает модель мира в его мозге. Во время перестройки нейросети человеку снятся необычные сны, как комбинации уже им пережитого с ошибочными промежуточными коэффициентами нейронных связей. Во время бодрствования (движения, охоты, еды, других активных действий) перестраивать веса связей опасно. Мозг содержит 1011 нейронов, 1015 связей нейронов, а организм состоит из 37,2 триллионов клеток, 4750*1027 атомов (показатель сложности модели), работая с очень большой скоростью (1 000 000 000 операций в одной клетке в 1 секунду, 100 триллионов операций в секунду – скорость работы мозга, скорость роста биологических тканей – 1 нм в сек), имея гигантскую размерность пространства (9 000 вкусовых рецепторов, около 6–7 млн колбочек и 110–125 млн палочек в сетчатке глаз, от 12 000 до 20 000 слуховых рецепторов и 100-200 рецепторов на 1 см2 кожи). Мозг человека поддерживает 1018 бит памяти. Мощнейшая машина!
Человек обладает 75 км нервов, по которым идут нервные импульсы со скоростью 90 м/сек, в головном мозге человека происходит 100 000 химических реакций в секунду, мозг генерирует в день больше импульсов, чем все телефоны мира.
Медуза имеет 800 клеток мозга, муха – 100 000, таракан – 1 миллион, кошка – 109, обезьяна – 7*109, человек – 86*109. В качестве входных (рецепторов) у человека выступают: фоторецепторы, хеморецепторы, терморецепторы, электрорецепторы, механорецепторы, осморецепторы, что соответствует зрению, слуху, осязанию, обонянию, чувству вкуса. Кроме этого, нельзя отрицать существование у человека чувства равновесия, силы тяжести, мышечных ощущений, способностей ощущать температуру, боль, голод, жажду.
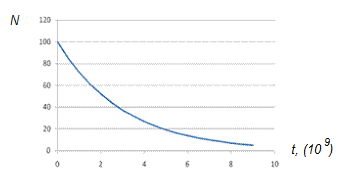
Реально перестройка сети идет по ниспадающей экспоненте (рис. 4.1) количества ошибок N: N ~ N0*et (109 тактов обучения t).
Интересно, что экспонентой быстро определяется грубое правильное решение (быстрый и ранний спад основного количества серьезных ошибок) и долгая тонкая настройка (длинный хвост экспоненты числа незначительных по величине ошибок). Мозг быстро схватывает общую суть в целом и долго усваивает детали, исключения. Сходство – быстро, различия – медленно.
|
|
| Рисунок 4.1 – Характерный экспоненциальный характер падения ошибок при обучении нейросети |
Впервые такую процедуру самонастройки сети осуществил Розенблатт в 1957 году, назвав такую сеть персептроном (от лат. perceptio - восприятие).
Задание
Необходимо построить нейронную сеть, которая будет осуществлять диагностику авиационного двигателя.
Двигатель – сложное техническое устройство и управлять им в силу его запутанных связей и сложных реакций – крайне непросто. Поэтому по внешним реакциям двигателя попробуем в целом понять его модель, не заглядывая внутрь, реализуя концепцию «черного ящика».
При испытаниях двигателей человек-эксперт давал субъективные оценки работы разных двигателей. Он обращал внимание на температуру изделия x1 и вибрацию x2. Однако эксперт не смог сформулировать закон связи технологических параметров двигателя с показателем опасности функционирования Y (опасно – (-1), безопасно – (+1)). Соответственно без такой модели нет возможности построить техническое устройство, сигнализирующее об опасности работы авиадвигателя по значениям его параметров.
|
|
| Рисунок 4.2 – Авиационный двигатель |
Построим такую модель. Точнее модель построит себя сама. Для этого нужен только материал для построения – сеть нейронов, которая будет самонастраиваться по мере поступления информации извне о том, «что такое хорошо и что такое плохо».
Имеются результаты 10 испытаний в виде таблицы 4.1 (базы данных).
Таблица 4.1 – Реакции объекта для настройки сети
| Пример | X1 (температура) | X2 (вибрация) | X3 (порог) | Y (опасность) |
| 1 | 1 | 1 | 1 | 1 (безопасно) |
| 2 | 9.4 | 6.4 | 1 | -1 (опасно) |
| 3 | 2.5 | 2.1 | 1 | 1 |
| 4 | 8.0 | 7.7 | 1 | -1 |
| 5 | 0.5 | 2.2 | 1 | 1 |
| 6 | 7.9 | 8.4 | 1 | -1 |
| 7 | 7.0 | 7.0 | 1 | -1 |
| 8 | 2.8 | 0.8 | 1 | 1 |
| 9 | 1.2 | 3.0 | 1 | 1 |
| 10 | 7.8 | 6.1 | 1 | -1 |
С помощью дельта-правила настроим нейросеть (построим модель) по предъявленным данным.
Построить модель нейросети означает найти значения весов ее связей (k1, k2, k3).
Предположим (для простоты), что сеть имеет вид одного нейрона: Y = f(x1, x2, x3). x3 – порог нейрона, оформленный в виде отдельного входа, х3 = 1. В качестве функции активации f возьмем функцию Y = sign(S) (рис. 4.3), где S = k1*x1 + k2*x2 + k3*x3.
|
|
| Рисунок 4.3 – Структура сети и функция активации нейрона sign(x) |
Примем случайным образом настройку сети: веса связей (k1, k2, k3), например,
(k1 = 0.75, k2 = 0.5, k3 = - 0.6).
Примем шаг обучения C = 0.2.
Примечание. Теории выбора наилучшего значения шага обучения не существует. Подбор величины шага (увеличение или уменьшение по ходу расчета) осуществляется подбором по виду функции ошибок.
Эпоха 1.
Шаг 1.
На первый пример из первой строки таблицы 4.1 (x1 = 1, x2 = 1, x3 = 1) при таких настройках весов связей (k1 = 0.75, k2 = 0.5, k3 = -0.6) сеть ответит: S = 0.75*1 + 0.5*1 + (-0.6)*1 = 0.65.
Далее: net = sign(S) = sign(0.65) = 1.
Эксперт ожидал от сети на эти значения X ответ: Y = 1.
То есть ответы эксперта и сети совпали: net = Y. Значит, переобучать сеть не надо.
Вектор весов связей остался прежним (k1 = 0.75, k2 = 0.5, k3 = -0.6).
Шаг 2.
На второй пример из второй строки таблицы 4.1 (x1 = 9.4, x2 = 6.4, x3 = 1) при таких настройках весов связей (k1 = 0.75, k2 = 0.5, k3 = -0.6) сеть ответит: S = 0.75*9.4 + 0.5*6.4 + (-0.6)*1 = 9.65.
Далее: net = sign(S) = sign(9.65) = 1.
А эксперт ожидал от сети на эти значения X другой ответ: Y = -1.
То есть ответы эксперта и сети НЕ совпали. Значит, переобучать сеть надо.
Обучение сети идет по «дельта-правилу»:
Или подставляя:
kновое := kстарое + C*(Y - net)*X,
Здесь dk – изменение значений вектора k (весов связей), C – шаг обучения, X – вектор значений состояний (сигналов). Приняли, С = 0.2.
Итак, dk1 = 0.2*((-1) - 1) * 9.4 = - 3.76, k1 новое := k1 старое + dk1 = 0.75 - 3.76 = -3.01.
То есть вес первой связи: k1 новое := - 3.01. Связь вместо возбуждающей, стала тормозной, так как сеть слишком оптимистично приняла первые значения весов. Сейчас она корректирует веса связей.
Продолжаем, dk2 = 0.2*((-1) - 1) * 6.4 = - 2.56, k2 новое := k2 старое + dk2 = 0.5 - 2.56 = -2.06.
То есть вес второй связи: k2 новое := - 2.06.
И еще раз, dk3 = 0.2*((-1) - 1) * 1 = - 0.4, k3 новое := k3 старое + dk3 = -0.6 - 0.4 = -1.
То есть вес третьей связи: k3 новое := - 1.
Вектор весов связей изменился и стал (k1 = -3.01, k2 = -2.06, k3 = -1).
Шаг 3.
На третий пример из третьей строки таблицы 4.1 (x1 = 2.5, x2 = 2.1, x3 = 1) при новых настройках весов связей (k1 = -3.01, k2 = -2.06, k3 = -1) сеть ответит: S = (-3.01)*2.5 + (-2.06)*2.1 + (-1)*1 = -12.84.
Далее: net = sign(S) = sign(-12.84) = -1.
А эксперт ожидал от сети на эти значения X другой ответ: Y = 1.
То есть ответы эксперта и сети НЕ совпали. Значит, переобучать сеть снова надо.
Обучение сети идет по «дельта-правилу»:
Итак, dk1 = 0.2*(1-(-1)) * 2.5 = 1, k1 новое := k1 старое + dk1 = -3.01 + 1= -2.01.
То есть вес первой связи стал: k1 новое := - 2.01.
Продолжаем, dk2 = 0.2*(1-(-1)) * 2.1 = 0.84, k2 новое := k2 старое + dk2 = - 2.06 + 0.84 = -1.22.
То есть вес второй связи: k2 новое := - 1.22.
И еще раз, dk3 = 0.2*(1-(-1)) * 1 = 0.4, k3 новое := k3 старое + dk3 = -1+ 0.4 = -0.6.
То есть вес первой связи: k3 новое := - 0.6.
Вектор весов связей снова изменился и стал (k1 = -2.01, k2 = -1.22, k3 = -0.6).
Обратите внимание, сеть сначала была чересчур оптимистична (положительные связи: k1 = 0.75, k2 = 0.5, k3 = -0.6) и на втором примере вместо Y = -1 выдала net = +9.65. И на этом (втором шаге) обучения сеть сильно этого несоответствия испугалась и свои до этого положительные значения связей стала резко менять на тормозные (отрицательные). Сила испуга dk пропорциональна входному сигналу Х, ошибке (Y - net) и темпераменту обучения С = 0.2. Все это и привело к большим тормозным значениям связей k1 = -3.01, k2 = -2.06, k3 = -1.
Однако на третьем шаге выяснилось, что сеть чересчур резко ушла в тормозные отрицательные значения весов связей, так как на входной сигнал третьего примера, когда ожидался положительный сигнал Y = 1, сеть очень пессимистично выдала отрицательный сигнал net = -12.84.
И поэтому сеть снова начала переобучаться, но уже в другую сторону, поднимая веса связей в сторону положительных возбуждающих значений с (k1 = -3.01, k2 = -2.06, k3 = -1) до (k1 = -2.01, k2 = -1.22, k3 = -0.6).
Далее аналогично вычисляем изменения весов связей, рассматривая примеры из остальных строк таблицы 4.1. Проделайте 7 оставшихся шагов самостоятельно. Найдите вектор весов связей на конец эпохи 1 (k1, k2, k3).
Так как после 10 шагов (10 строк таблицы, 10 примеров) выяснится, что сеть перестраивалась 6 раз (допустила шесть ошибок), то надо провести эпоху 2, рассчитывая примеры снова от 1 до 10 с новыми (k1, k2, k3), меняя их далее.
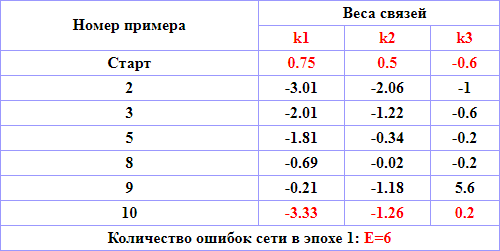
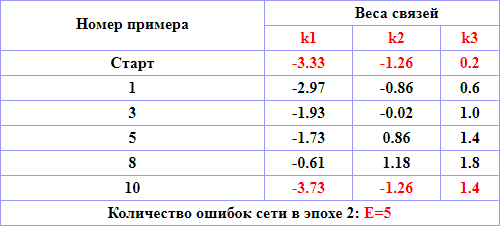
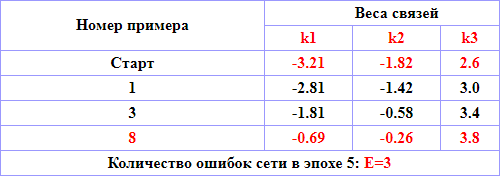
Таблица 4.2 – Расчет значений коэффициента связей нейросети, эпоха 1
|
Вычисляя коэффициенты весов связей нейрона, можно одновременно геометрически проиллюстрировать пространство входных и выходных сигналов в осях (х1,х2). Посмотрим это на примере итерации 2:
| Пример | k1 | k2 | k3 |
| 2 | -3.01 | -2.06 | -1 |
Очевидно, что уравнение -3.01*х1 - 2.06*х2 - 1 = 0, которое получилось в результате второй итерации первой эпохи, представляет собой прямую линию, которая делит пространство (x1 - температура, x2 – вибрация, х3 – порог в уравнении нейрона: k1*x1 + k2*x2 + k3*x3 = 0, x3 = 1) на две части:
-3.01*х1 - 2.06*х2 - 1 > 0
-3.01*х1 - 2.06*х2 - 1 < 0
Одна часть полупространства соответствует безопасным (Y>0) условиям эксплуатации двигателя (пары x1 и x2), вторая – опасным (Y<0). На рисунке 4.4 показана эта прямая линия -3.01*х1 - 2.06*х2 - 1 = 0 под номером 2.
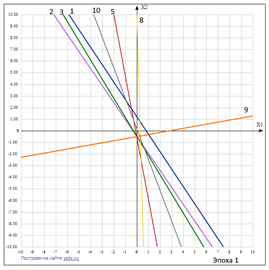
По мере обучения нейросети значения коэффициентов ее связей меняются. Значит, меняется и положение прямой линии. Она вращается и смещается. На рис. 4.4 видны изменения положения прямой во время эпохи 1, соответствующие примерам 1, 2, 3, 5, 8, 9, 10.
Поскольку сеть ошибается (6 ошибок за эпоху 1), то ее продолжают обучать, прогоняя еще раз все примеры заново с уже скорректированными значениями коэффициентов связей. Это называется эпохой 2.
Повторение эпох происходит до тех пор, пока сеть не обучится. Признаком обученности сети является факт отсутствия изменений значений вектора весов связей (k1, k2, k3) при проверке всех десяти примеров таблицы 4.1. Количество ошибок E сети будет постепенно уменьшаться и достигнет значения нуля.
|
|
| Рисунок 4.4 – Положение разделяющего правила нейрона во время прохождения обучения эпохи 1 |
Признак о постепенном обучении работает, если параметры обучения выбраны удачно.
Однако следует иметь в виду. Если шаг обучения С большой, то сеть начнет разбалтываться. В этом случае количество ошибок от эпохи к эпохе не уменьшается, а остается постоянным или увеличивается. При этом ошибки появляются все время в разных примерах (эффект «то это помним, то другое»). Кривая ошибок колеблется вверх-вниз и не идет монотонно вниз.
Если значение шага обучения С слишком мало, то сеть обучается слишком медленно. Ей приходится многократно повторять одни и те же примеры, чтобы она сменила реакцию на них с неправильной на правильную. Кривая ошибок постоянна и не падает.
В таблицах 4.3 - 4.7 показаны промежуточные результаты расчета. Всего сеть сделала 19 ошибок за все время обучения, при этом количество ошибок снижалось по мере того, как сеть обучалась.
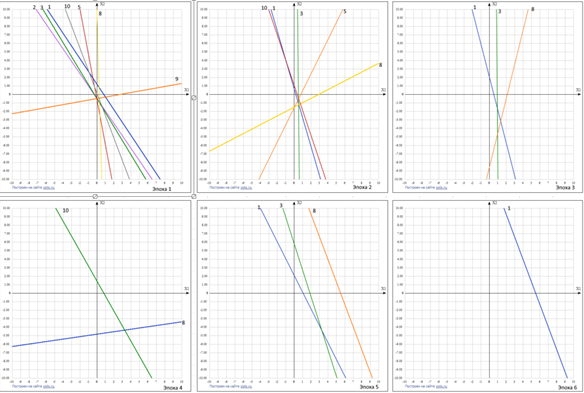
На рисунках 4.5 - 4.9 показано как изменяется линия «модель нейрона» в процессе расчета (обучения), то есть перестройки весов связей (меняется наклон и смещение линии). Номер линии указывает на номер примера в базе данных. Оси координат – входные сигналы (рецепторы).
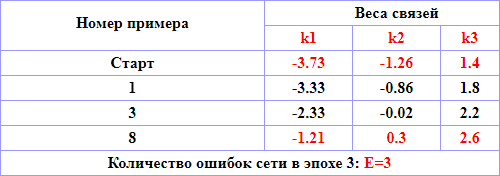
Таблица 4.3 – Расчет значений коэффициента связей нейросети, эпоха 2
|
|
|
| Рисунок 4.5 – Положение разделяющего правила нейрона во время прохождения обучения эпохи 2 |
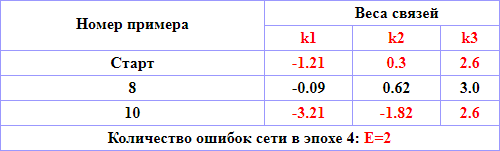
Таблица 4.4 – Расчет значений коэффициента связей нейросети, эпоха 3
|
|
|
| Рисунок 4.6 – Положение разделяющего правила нейрона во время прохождения обучения эпохи 3 |
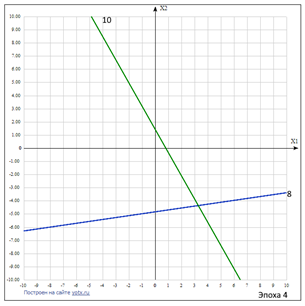
Таблица 4.5 – Расчет значений коэффициента связей нейросети, эпоха 4
|
|
|
| Рисунок 4.7 – Положение разделяющего правила нейрона во время прохождения обучения эпохи 4 |
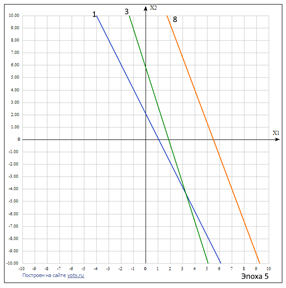
Таблица 4.6 – Расчет значений коэффициента связей нейросети, эпоха 5
|
|
|
| Рисунок 4.8 – Положение разделяющего правила нейрона во время прохождения обучения эпохи 5 |
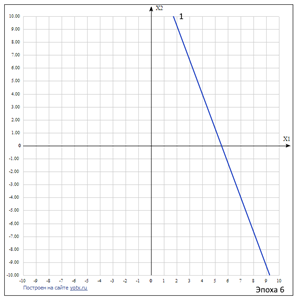
Таблица 4.7 – Расчет значений коэффициента связей нейросети, эпоха 6
|
|
|
| Рисунок 4.9 – Окончательное положение разделяющей линии нейрона, обученного на 10 примерах в течение 6 эпох |
|
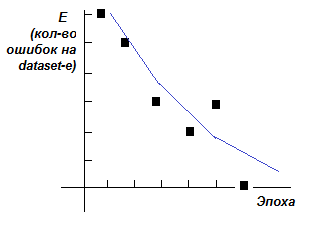
|
| Рисунок 4.10 – График количества ошибок, сделанных сетью, в зависимости от количества эпох обучений. По мере обучения (с ростом номера эпохи) количество ошибок уменьшается |
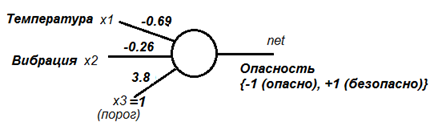
Ответ задачи: S = -0.69*х1 - 0.26*х2 + 3.8 при S>0, S<0, S=0
Y = sign(-0.69*х1 - 0.26*х2 + 3.8) при Y = -1, Y = 0, Y = +1
или в терминах предметной области (математическая модель):
Опасность = sign(-0.69*Температура – 0.26*Вибрация + 3.8)
|
|
| Рисунок 4.10 – Сеть с настроенными весами связей |
Примечание. Появление веса связи нейрона, отличного от 1, означает, что на деле у реального нейрона прорастут дополнительные отростки-связи. Две следующие схемы эквивалентны, а порог внутри нейрона равен 0.
|
|
| Рисунок 4.11 – Вид нейрона с изменением значений связей |
Дробные веса связей, например, {-0.69, -0.26 и 3.80} означают, что у нейрона вырастет {69, 26, 380} отростков у соответствующих связей. Отрицательные веса – связь будет тормозящей, положительные – связь будет возбуждающей.
Геометрическая интерпретация результата
При Y = 0 имеем -0.69*х1 - 0.26*х2 + 3.8 = 0 и X2 = 14.6*x1 - 2.65 – разделяющее правило.
Строим график в осях {x1, x2} и в поле устанавливаем точки-примеры-экземпляры классов (рисунок 4.12).
Обозначаем классы. Видно, что примеры опасной работы двигателя (2,4,6,7,10) из таблицы 4.1 оказались по одну сторону от разделяющего правила, а примеры безопасной работы (1, 3, 5, 8, 9) – по другую. Ошибок нет. Сеть настроена.
|
|
| Рисунок 4.12 – Расположение разделяющего правила (прямой линии) в результате обучения нейросети и областей реакции сети (классов) |
Самостоятельное задание
Дойдите до конца обучения с этим или другим начальным вектором значений весов связей k с этим или другим значением шага С.
Найдите окончательный вид вектора (k1, k2, k3). Приведите в отчете промежуточные его значения на шагах и эпохах. Подсчитайте количество ошибок Е (перестроек) сети в каждую эпоху. Нарисуйте график количества ошибок E от номера эпохи.
Нарисуйте в осях (X1, X2) график S(X1, X2), выразив x2 через x1 из получившегося уравнения S = k1*x1 + k2*x2 + k3*x3, где (k1, k2, k3) – найденные Вами числа, x3 = 1, S = 0.
На график по координатам (X1, X2) нанесите положение 10 точек из таблицы 3. Посмотрите, как расположилась прямая линия S = 0 относительно точек. Выпишите математическую модель, выведенную сетью.
ВЫВОД: В процессе обучения нейросети линия, разделяющая классы, смещалась и вращалась (рис.4.13) в пространстве рецепторов до тех пор пока не установилась так, чтобы разделить (рис.4.12) по одну сторону (полуплоскость) экземпляры одного класса, а по другую – второго класса. Сеть научилась отличать одни ситуации от других.
|
|
| Рисунок 4.13 – Последовательное изменение положения разделяющей линии (правила) |
Отметим скорость, с которой менялись связи.
|
|
| Рисунок 4.14 – Скорость изменения количества ошибок |
Сделайте вывод и приведите его в отчете:
- как изменяется положение прямой S = 0 в процессе обучения сети,
- в какое положение прямая стремится в конце обучения,
- каков закон связи температуры и вибрации авиадвигателя,
- как определить опасность в зависимости от температуры и вибрации двигателя,
- как быстро меняется количество ошибок сети E в процессе обучения,
- как выглядит окончательно сеть после обучения (веса связей).
Объясните роль весовых коэффициентов связей нейронов сети. Объясните роль значения шага C (очень большой шаг, очень маленький шаг).
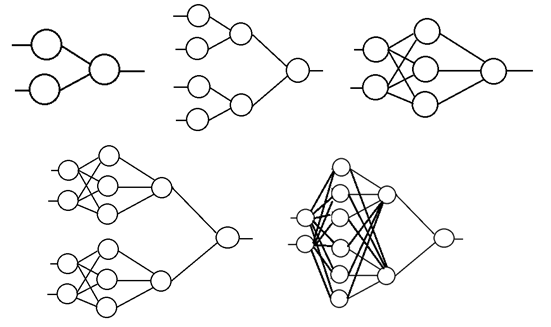
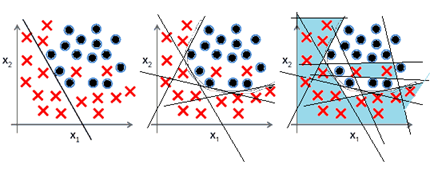
Нарисуйте как выглядит (гипотетически) график и области, в которых сосредоточены точки примеров, при двух нейронах сети, при трех нейронах сети, в случае однослойной сети, двухслойной сети, трехслойной сети. Как меняются рисунки при увеличении числа рецепторов? Как в итоге представлены знания в мозге человека?
Достоинства Перцептрона
1. Перцептрон не знает, как он это делает, но он это делает.
2. Перцептрон решает любую задачу одним и тем же методом.
3. Метод крайне прост.
4. Перцептрон может переучиться, если мир изменится.
5. Перцептрон находит модель, а не запоминает конкретные случаи (таблицу данных), обобщая информацию до уравнения.
6. Перцептрон может на основании построенной им модели отвечать на новые вопросы и порождать новые данные, а не только воспроизводить данные, на которых он обучался.
7. В основе перцептрона лежит естественная простая парадигма: «За правильное поощряют, за неверное – наказывают», «Повторение – мать учения».
8. Перцептрон строит модель окружающего мира. Модель может слегка отличаться от модели реального мира. Перцептрон реализует свое поведение с определенной точностью. Отличие модели мира от модели мира, построенной перцептроном, может быть количественно оценено. Перцептрон обобщает информацию, от данных переходит к уравнениям, от точек к областям, от экземпляров к классам, от арифметики к алгебре, от чисел к буквам-переменным, от фактов к правилам, законам, знаниям.
9. Перцептрон – гипертело в гиперпространстве рецепторов. Нейроны – это гиперплоскости, разделяющие гиперпространство рецепторов на области-классы. Примеры – это экземпляры класса, точки в гиперпространстве. Гипертело – смысл. Построение гипертела – процесс понимания свойств и устройства мира.
10. Мозг устроен просто (сложение, умножение и функция Хэвисайда – простейшая нелинейность), а ведет себя сложно. Мозг осуществляет сдвиг и вращение гиперплоскостей и логические функции с гипертелами.
11. Сеть нейронов представляет собой операцию скалярного умножения вектора входных сигналов и вектора весов нейросети. По определению, скалярное произведение двух векторов Х и К – косинус между векторами сигналов мира X и состояния обучаемого K, мера похожести Х и К.
12. Нейросеть – это система, то есть элементы X и связи K, демонстрирующая новые свойства, отличные от свойств составляющих ее элементов. Свойством здесь является гипертело, которое образуется уравнениями (неравенствами) нейронов-элементов.
13. Память интеллектуальной системы находится в связях между понятиями и представляет собой систему уравнений окружающего мира. Информация – это связи. Связи – это информация. Связь – это число, сомножитель между источником и приемником информации.
14. Связи перцептрона можно отразить матрицей. Знания о мире – матрица. С матрицами возможны операции. Матрица – это гипертело.
15. Перцептрон устойчив к повреждениям, так как умеет доучиваться и переучиваться после того, как часть нейронов вышла из строя или если среда изменила свои правила.
16. В скрытых слоях перцептрона скрывается обобщение.
17. Чем больше знает перцептрон, тем легче ему решить новую незнакомую задачу. Знания- это правильно настроенная матрица, гипертело, которое соответствует правильно построенной системе уравнений.
18. Знания – это модели, а не данные. Модели – это уравнения. Алгоритмы – это суть процесс решения задач, траектории перехода от известных величин к неизвестным. Алгоритм имеет меньшую ценность, нежели модель. Модель порождает алгоритмы – последовательность действий, приводящую к ответу на вопрос, решению. Перцептрон создает программы решения задач, но сам является моделью окружающего мира, которую сам создает.
19. Много ошибок – процесс обучения идет быстро. Мало ошибок – процесс усвоения деталей замедляется.
20. Перцептрон имитирует человеческую мыслительную деятельность, которая появилась эволюционно.
Занятие 5. На что способны нейронные сети
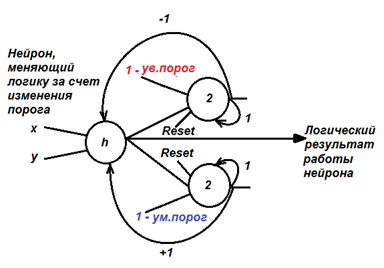
Как нейрон меняет вес своей связи
За счет дополнительных сигналов (увеличить порог на 1, уменьшить порог на 1), поступающих от окружающей среды (от дельта-правила), подаваемых на линейчатый нейрон, можно изменить выходной сигнал вспомогательных нейронов с памятью, поскольку такие нейроны держат сигнал, отслеживая его уровень. Меняя вес связи, мы, таким образом, меняем логику работы нейрона, подстраиваем его модель под примеры. Еще раз напомню, что роль порога играет здесь уровень дополнительной связи.
|
|
| Рисунок 5.1 – Вспомогательный нейрон меняет (увеличивает или уменьшает) порог срабатывания основного нейрона |
Или другой вариант изменения весов связи в нейросети, используя ступенчатые нейроны. С помощью счетчика сигналов можно менять величину сигнала, постепенно накапливая значение суммы в счетчике (рис.5.2).
|
|
| Рисунок 5.2 – Счетчик количества входных сигналов нарастающим итогом |
Один счетчик может накапливать сигналы, имеющие смысл положительного увеличения (1, 2, 3, 4, …). Второй счетчик такой же может накапливать сигналы (1, 2, 3, 4,…), имеющие смысл отрицательной суммы. Далее отдельная схема сравнивает суммы, приходящие с двух счетчиков, находя разность двух значений. Этот результат интерпретируется для нейрона как порог. Изменение значения порога меняет логику нейрона.
Важное примечание
За счет изменения значения веса связи k нейрон реализует операцию умножения сигналов k*X, где Х – вход нейрона. Изменение величины порога реализуется с помощью счетчика сигналов (рис. 5.2). Меняя значение связи, можно получить произведение любых сигналов k и X.
Задание
Нарисуйте сеть, которая вычисляет функцию y = 5x3 - 2x2 + 6x - 2, где Y - выход сети, x – вход.
Нарисуйте сеть, которая вычисляет функцию y = 3*x*z - 2x + x2z.
Обсуждаем и обобщаем результаты – «на что способны нейронные сети»
Представим себе однослойную сеть (рис.5.3).
|
|
| Рисунок 5.3 – Структура однослойной сети и ее свойства |
Она хорошо различает два компактных класса. Пример первого класса отмечен на рисунке 5.3 крестиками, второго – ноликами.
Нейрон – разделяющая линия между классами. Настройка линии – это ее вращение (коэффициенты k связей линейной формы) и сдвиг (порог) в осях координат (рецепторов).
Проблемой является ситуация (задача Минского) исключающего ИЛИ: как одной прямой отделить примеры «Х» от примеров «0» (рис.5.4), удовлетворяющие таблице истинности этой операции? Как бы Вы не проводили прямую линию, она не сможет отделить точки (экземпляры) области (класса) «Х» от точек области «О».
|
Таблица 5.1 – Таблица истинности операции «Исключающего ИЛИ»
| X | Y | Исключающее ИЛИ (X, Y) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
|
|
| Рисунок 5.4 – График и таблица, иллюстрирующие специфическое распределение четырех примеров, демонстрирующих логическую функцию «исключающее ИЛИ» |
Внимание: данное разделяющее правило ошибается и решить поставленную задачу не может!!!
Исходя из таблицы истинности, Минский записал систему ЛИНЕЙНЫХ уравнений этой задачи:
k1*1 + k2*1 = 0
k1*1 + k2*0 = 1
k1*0 + k2*1 = 1
k1*0 + k2*0 = 0
k1, k2 - ?
Естественно, решения в линейной форме такая система не имеет!
Поскольку такое разделение классов одним нейроном невозможно – нельзя разделить двухмерное пространство на 4 области одной прямой линией, – то поставленный Минским вопрос остановил развитие нейронных сетей на несколько лет.
«Нейросети ограничены и потому неинтересны», - так прозвучал ответ.
Однако, если подумать, то можно предложить несколько решений задачи Минского.
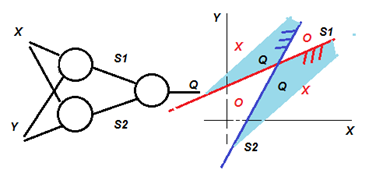
1. Ввести второй нейрон и с ним вторую прямую линию (рис.5.5). Две прямые линии, пересекаясь, разделят пространство на 4 подпространства. Нейрону Q остается решить, кем ему быть: «ИЛИ» или «И» операцией (см. упражнение 1). Настройка связей сети показана на рис.5.6. То есть введение двухслойной сети позволяет решить проблему Минского. Для сравнения на рис.3.18 можно посмотреть реализацию на сети операции И.
|
|
| Рисунок 5.5 – Два нейрона и две их прямые делят пространство на 4 области (4 класса), нейрон Q реализует логическую функцию исключающее ИЛИ (штрихами обозначены области S1>0 и S2>0, закрашенная область – (S1>0)|(S2>0)) |
|
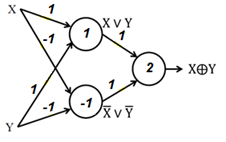
|
| Рисунок 5.6 – Реализация исключающего ИЛИ на двухслойной сети нейронов |
В случай, если нейрон второго слоя реализует функцию «ИЛИ», то можно описать область типа «бабочка» (рис.5.5).
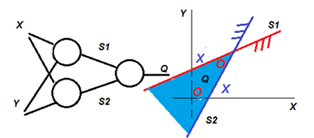
Если нейрон Q реализует логическую функцию «И», то два нейрона первого слоя, деля пространство (X, Y) на 4 подпространства, дают возможность описать класс с топологией «клин» (рис.5.7).
|
|
| Рисунок 5.7 – Два нейрона и две их прямые делят пространство на 4 области (4 класса), нейрон Q реализует логическую функцию И (в закрашенной области одновременно (S1>0) И (S2>0)), то есть: Q = ((S1>0)&(S2>0)) |
2. Второй вариант решения проблемы Минского состоит в ведении двух подклассов одного класса (рис.5.8).
|
|
| Рисунок 5.8 – Два нейрона и две их параллельные прямые делят пространство на 3 класса |
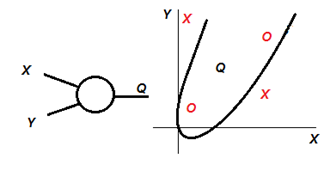
3. Третий вариант – введение в рассмотрение нелинейного нейрона (рис.5.9).
|
|
| Рисунок 5.9 – Сеть с нелинейным нейроном (параболическая функция сумматора) |
4. Ввести дополнительный признак Z, отделив плоскостью один класс от другого (рис.5.10). То, что нельзя сделать в двухмерном пространстве, можно сделать в пространствах большей размерности (трех, четырех, …). Но признак Z (рецептор) должен быть удачно подобран.
|
|
| Рисунок 5.10 – Три рецептора (трехмерное пространство) и один нейрон помогают разделить исключающее ИЛИ на два класса. Точки «0» находятся за плоскостью, отделены плоскостью нейрона от наблюдателя. Точки «Х» находятся между плоскостью нейрона и наблюдателем |
Очевидно, что математическая конструкция
S = k1x1 + k2x2 + … + kixi + … + knxn (скалярное произведение векторов k и x)
Y = one(S - h) или Y:=(S>=h) (функция sign, if)
обеспечивает большое разнообразие представляемых ею функций и откликов сети. А именно, первое выражение – линейная часть этой конструкции, второе (функция Хэвисайда) – простейшая нелинейность. Набор цепочки «линейность-нелинейность-линейность-нелинейность-…» - своеобразный базис для статических конструкций, в котором необходимо настроить вектор весовых коэффициентов {k}.
Задание
Для сетей, топология которых задана на рисунке 5.11, нарисуйте геометрическую интерпретацию пространства классов, которое порождает каждая из представленных сетей (в общем виде).
|
|
| Рисунок 5.11 – Различные варианты задания нейронных сетей |
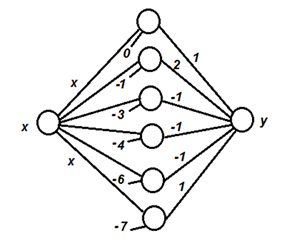
Разберем, как составить сеть, которая будет соответствовать какой-либо заданной наперед функции Y = f(X) (рис.5.12).
|
|
| Рисунок 5.12 – Функция для описания сетью |
Очевидно, что у сети один вход (X) и один выход (Y). Представим запись функции в математическом виде: Y = 1*(x>0) + 2*(x>1) + (-1)*(x>3) + (-1)*(x>4) + (-1)*(x>6) + 1*(x>7).
Или, используя функцию Хэвисайда:
Y = one(x) + 2*one(x - 1) - one(x - 3) - one(x - 4) - one(x - 6) + one(x - 7).
Или, приводя к нормальной форме:
Y = 1*(-x<=0) + 2*(-x+1<=0) + (-1)*(-x+3<=0) +(-1)*(-x+4<=0) + (-1)*(-x+6<=0) + 1*(-x+7<=0).
В результате получаем сеть (рис. 5.13).
|
|
| Рисунок 5.13 – Сеть, моделирующая функцию Y = f(X) |
Задание. Составьте самостоятельно сеть для функции на рис. 5.14.
|
|
| Рисунок 5.14 – Функция для описания сетью |
Часто возникает вопрос об изначальном задании размера сети. Маленькая сеть может не усвоить сложность заданных примеров (смотри пример Минского). Большая сеть – избыточна. А значит, долго обучается, плохо обобщает, излишне учитывая шум.
|
|
| Рисунок 5.14.1 – Недоученная, нормальная и переученная сеть |
Большую роль играет соотношение продольного (количество слоев) и поперечного (количество нейронов в слое) размера сети.
Пример:
Изучая английскую грамматику, требуется знать огромное число понятий. В этом случае однослойная широкая нейронная сеть работает намного лучше, чем глубокая нейронная сеть, которая значительно меньше.
Но в случае моделирования преобразования Фурье ученик (нейронная сеть) должен быть глубоким, потому что не так много понятий, которые нужно знать, но каждое из них достаточно сложное и требует глубокого понимания.
Нерешенные вопросы
До сих пор теоретически не решены вопросы соотношения сложности сети и сложности отображаемого ею мира.
Можно научить сеть складывать числа: 2+5-7, 3+1=4 и так далее. Например, на ста подобных примерах. Вопрос заключается в том, сможет ли сеть после обучения сложить два произвольно длинных числа: 1000023 и 564117?
Известно, что после упражнения в детстве с константами (2 карандаша, 4 яблока, 6 столов) человек приходит к понятию «переменная» и в дальнейшем свободно оперирует им. Как выглядит нейросеть, умеющая это делать?
Может ли сеть решить задачу: если x=a+b, то a=?
Необходимо построить нейросеть, умеющую вычислять длину гипотенузы прямоугольного треугольника по теореме Пифагора: C=√(A*A+B*B). Проблема заключается в том, что каждый нейрон представляет собой прямую линию (гиперплоскость) в пространстве рецепторов. В то время как в данном случае требуется обеспечить нелинейную кривую. Конечно, можно представить себе приближенно окружность как множество отрезков одной ломаной. Другой выход будет состоять в том, чтобы объявить сумматор как S=k1*A+k2*B+k3*A*B+k4*A*A+k5*B*B. Однако, что делать, если потребуются функции третьей степени, четвертой и т.п.? А также степенные функции. В любом случае проблема состоит в том, чтобы ввести в состав нейрона не только сложение, но и умножение сигналов. Актуальной проблемой является также представление в сети обратных операций (деление, извлечение степени).
Модель технического устройства в виде сети
Любое статическое техническое устройство – это функция в системе координат входных-выходных переменных: Y = f(X), где f - один большой закон, собранный подстановкой из простейших законов.
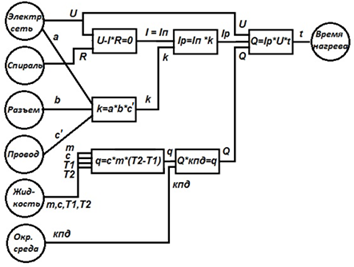
Например, составим модель электрического чайника из законов Ома, Фурье, а также геометрических и логических особенностей конструкции (рис. 5.15).
|
|
| Рисунок 5.15 – Модель электрического чайника |
Модель электрического чайника имеет вид:
R*c*m*(T2 - T1) - U2*q*a*b*c’*t = 0.
Подстановкой одних законов в другие согласно топологии собранной каскадной модели получаем функцию выхода относительно входа (входов) t = f(U, R, a, b, c, m, c’, T1, T2, кпд):
t = R*c*m*(T2 - T1)/(U2*q*a*b*c’).
Или в общем неявном
F(R, c, m, T2, T1, U, q, a, b, c’, t) = 0
и в явном виде
t:=f(R, c, m, T2, T1, U, q, a, b, c’).
Используя линейчатый нейрон (рис.1.4.1.б), постройте сеть, моделирующую электрический чайник.
Обобщение
Нейросеть – геометрическая область в системе координат ощущений, функция. Нейросеть может настроиться на любую функцию, имитировать свойства любого устройства. Нейросеть может управлять любым устройством. Нейросеть может отыскивать другие устройства, отбирая нужные ей по их поведению, так как поведение – это функция.
Обратные связи в нейросети обеспечивают динамические свойства системе, производные, нелинейности, память, циклы.
Нейроны соответствуют также базису программирования: сложение, умножение, условный выбор (IF), цикл (динамические нейронные сети), переход (проращивание связей между слоями нейросети). Ячейки памяти – нейроны с обратными связями.
Обучение сети, заключающееся в настройке весовых коэффициентов, соответствует операции мультипликации (скалярное произведение сигналов). Происходит умножение сигналов входов Х от окружающей среды (соответствуют реальности, экспериментальным данным) на веса связей k (соответствуют памяти, виртуальности, нашим приближенным теоретическим представлениям о реальности, являются моделью реальности): k*X. Операция умножения по смыслу соответствует вычислению степени похожести реальности на виртуальность. Чтобы это понять, достаточно вспомнить метод косинусов. При изменении значений весов виртуальность подтягивается к реальности, а теоретическая модель к экспериментальным данным.
Настройка веса связей – это подстройка виртуальности под реальность, в результате строится модель реального мира.
Выводы.
Принцип Эшби. Сеть не может решить задачу, если количество нейронов в ней не позволяет построить корректное разделение классов. Мощность задачи должна быть не больше мощности сети. Управляющая система должна быть мощнее управляемой. Начальник должен быть умнее (сложнее организован) подчиненного.
Если принцип Эшби не выполняется, то сеть начнет ловить частные случаи и без конца перестраиваться. Количество ошибок сети на dataset-е будет не равно нулю.
Чтобы сеть смогла решить задачу, она должна быть больше определенного размера.
Избыточно мощная сеть порождает не минимальные законы функционирования. Например: правило y = x1 + 3*x2 + 4 может быть представлено y = (2*x1 + 6*x2 + 8)/2 + x1 - x1 + 7 - 4 - 3 и т.д..
Понимание мира мозгом связано с минимально возможной не ошибающейся сетью (Е=0). Ощущение связано с рецепторами.
Количество входов сети (рецепторов) - размерность пространства.
Количество слоев сети – сложность гиперобласти в гиперпространстве рецепторов, сложность (порядок) задачи. Сложность окружающего нас мира – суть количество рецепторов и сложность топологии гиперпространства, образуемого ее размерностью и примерами.
Сложность мира – это сложность гиперфигуры в гиперпространстве, то есть количество ее вершин и граней. Но одновременно, это количество сложений, умножений и количество переменных – сложность получившейся системы уравнений, описывающей мир. Вершины гипертела – переменные, операции - связи.
Нейрон – предикат, функция. Точнее, нейрон – нелинейная функция. Если бы нейрон был только сумматором и не содержал активационной нелинейной функции, то сеть оставалась бы однослойной (линейной) при любом ее количестве слоев. Сеть может создавать любые сколь угодно сложные гиперобласти (фигуры) в гиперпространстве рецепторов при наличии соответствующего количества слоев.
Занятие 6. Обобщение темы
«Понимание мира и его ощущения в нейронной сети. Образование новых сложных понятий»
Задание
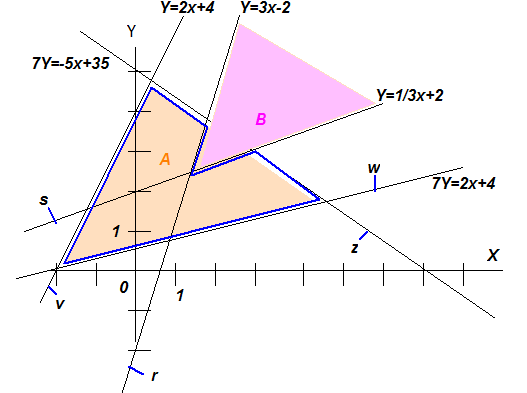
Проиллюстрируйте геометрически область допустимых значений выхода С уже настроенной нейронной сети (рис.6.1) в области ее входных сигналов X и Y. Выделите заливкой область, в которой нейронная сеть будет выдавать выходной сигнал, равный 1. Обозначьте на рисунке буквами сущности: X, Y, r, s, z, v, w, A, B, C.
|
|
| Рисунок 6.1 – Пример нейронной сети, порождающей функцию С=f(X,Y) |
Найдите и нарисуйте функцию С = f(X, Y). Приведите вид математической модели сети.
Примечание.
При описании сети используйте стандартную запись: q = (ax + by + c > 0), которая означает, что переменная q (выход нейрона) равна 1, если неравенство выполняется, и q равна 0, если неравенство не выполняется.
6.1. Конструктор нейросетей
За основу возьмем конструкции И, ИЛИ, НЕ. Как известно, из таких конструкций можно создать любую статическую функцию.
- Любая база статических данных может быть представлена логической функцией в пространстве атрибутов-рецепторов {0,1}.
- Любая база данных – статическая функция.
- Любая логическая функция – комбинация функций И-ИЛИ-НЕ.
- Нейрон с функцией «И»: С = A&B, C = (A + B>=2) = (A + B - 2>=0) = (-A - B + 2<=0)
- Нейрон с функцией «ИЛИ»: C = A!B = (A + B>=1) = (A + B - 1>=0) = (-A - B + 1<=0)
- Нейрон с функцией «НЕ»: C = ¬A = (1 - A>=1) = (1 - A - 1>=0) = (-A>=0) = (A<=0)
6.2. Алгебра нейросетей
Возьмем произвольную нейронную сеть, например трехслойную плюс слой рецепторов (рис.6.1). Пороги нейронов вынесем в качестве дополнительного слагаемого сумматора – дополнительной связи нейрона. Неравенство «>» при необходимости приведем к неравенству «<». Опишем математически эту нейросеть системой уравнений.
Таким образом:
| z = (5x + 7y <= 35) или z = (5x + 7y - 35 <= 0) | (1) |
| v = (-2x + y <= 4) или (-2x + y - 4 <= 0) | (2) |
| w = (-2x + 7y >= 4) или w = (-2x + 7y - 4 >= 0) или w = (2x - 7y + 4 <= 0) | (3) |
| A = z&v&w = (z + v + w >= 3) или A = (-z - v - w + 3 <=0 ) | (4) |
| r = (-3x + y <= -2) или r = (-3x + y + 2 <= 0) | (5) |
| s = (-x + 3y >= 6) или s = (-x + 3y - 6 >= 0) или s = (x - 3y + 6 <= 0) | (6) |
| B = r&s = (s + r >= 2) или B = (s + r - 2 >= 0) или B = (-s - r + 2 <= 0) | (7) |
| C = A&НЕ(B) = (2A - B >= 2) или C = (2A - B - 2 >= 0) или C = (-2A + B + 2 <= 0) | (8) |
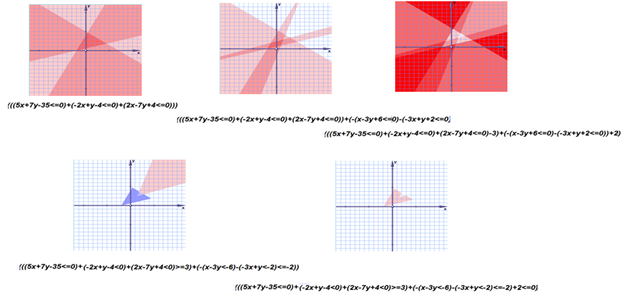
6.3. Геометрия нейросетей
Геометрически 1, 2, 3 уравнение этой системы представляют собой неравенства, которые в пространстве x, y отсекают полуплоскости прямыми линиями типа ax + by + c = 0 и, пересекаясь между собой, образуют области, в которых z (или v, или w) принимают значения 0 или 1. Сложение z, v, w между собой в различных частях пространства x, y (при различных значениях переменных x,y) дают различные результаты: 1, 2 или 3 (рисунок 6.2.а).
Нейрон с выходом А во втором слое сети (уравнение 4) реагирует в частности на значение этой суммы z+v+w, возбуждаясь (А = 1) или нет (А = 0). Возбуждается этот нейрон в области ярко красного треугольника.
На рисунке 6.2.б добавлены полуплоскости неравенств 5 и 6 и показаны дополнительные области образованные суммой переменных r и s в уравнении 7. Области представляют собой трехмерную функцию в пространстве координат x, y, принимающую значения от 0 до 5 в разных частях пространства x*y, что указано цветом (рисунок 6.2.в).
|
|
| Рисунок 6.2. – Геометрическая иллюстрация сигналов внутри нейросети |
Уравнения 4 и 7 с заданными неравенствами выделяют две области (синяя и розовая на рисунке 6.2.г) А и В, которые соответствуют выходам нейронов второго слоя нейросети. Переменные А и В принимают значения 0 или 1 каждая в зависимости от области пространства, то есть значений рецепторов x, y.
Уравнение 8, содержащее значения А и В в линейной комбинации -2А + В + 2<=0 реализует, для примера, логическую функцию С = А И НЕ(В) (А без В) на области допустимых значений аргументов {А, В} = {0, 1}, что можно проверить на таблице истинности.
Таблица 6.1 – Таблица истинности операции вычитания А без В
| А | В | С = А И НЕ(В) = -2А+В+2<=0 |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Это значит, что результирующая область (розовая фигура, соответствующая значениям С=1) имеет вид, показанный на рисунке 6.2.д.
В итоге формула сети (область С с синим контуром) имеет вид (рисунок 6.3):
C = ((-2(-(5x + 7y<=35) - (-2x+y<=4) - (2x-7y<=-4)<=-3) + (-(x-3y<=-6) - (-3x + y<=-2)<=-2))<=-2)
Сколько выходов будет иметь сеть, столько будет подобных выражений-двойников. Выражения предназначены для удобства алгебраического исчисления условий функционирования сети и арифметического вычисления состояния сети.
|
|
| Рисунок 6.3. – Область существования выходного сигнала нейросети (область выделена по контуру синим цветом) |
6.4. Понимание мира нейросетью
Фактически, обобщая, сеть задает гиперобласти (фигуры) в пространстве рецепторов x, y. При этом образование гиперфигур соответствует классам, то есть сложным понятиям, образующимся в сознании сети. Рецепторы соответствуют входным переменным – ощущениям. Таким образом, сеть имитирует понимание классов реакций мозга в пространстве рецепторов (X, Y) – ощущений, то есть связывает простейшие ощущения, поступающие из окружающего мира, со сложным пониманием устройства мира логической формулой - моделью.
Заметим, что x, y – признаки, тип рецептора. Например, х - размер, y - вес.
Значения, которые принимают x, y – свойства, сигнал с рецептора. Например, легкий (y = 0), тяжелый (y = 1), средней тяжести (y = 0.3). В языке описываются прилагательными.
z, v, w – признаки более абстрактного характера. Например, весо-размер. Эти признаки выражаются зависимостями (например, 5x + 7y = 35) неравенствами (например, 5x + 7y - 35<=0), задающими области в пространстве ощущений, поля сложных свойств. Умножения выполняют роль операции И, сложение – ИЛИ. Поэтому определение «кошка», составленное как сложная логическая функция из комбинации И-ИЛИ-операций, представляет собой сеть, каждый нейрон которой – суть уравнение-неравенство, закон. А вся сеть - комбинация законов, модель.
Такие линейные формы соответствуют скалярному произведению вектора ощущений Х на вектор весов понимания k, то есть косинусу угла между ощущениями и пониманием мира (рассматриваются на практике «Классификация. Косинусы»). Косинус – это мера похожести перемножаемых векторов величин.
Во внутренних областях нейросети это принимает форму скалярного произведения вектора понимания на вектор понимания следующей абстракции – образование все более сложных абстракций в представлении сети.
Пересечение свойств задает объекты, элементы. Например, зеленое И круглое И сладкое – это яблоко. Такими в нашей сети являются выражения для А и В, второй слой сети. Поля свойств образуют выпуклые фигуры-понятия, объекты, элементы, описываемые именами существительными.
Третий слой нейросети указывает на отношения (связи) объектов с помощью действий И, ИЛИ, НЕ. Третий слой образует произвольные фигуры в пространстве ощущений, в том числе и вогнутые. По сути третий слой сети – функция, действие, глагол. А также сложные понятия: кошка без шерсти.
После того как определены объекты и связи между ними, появляется система. По определению система – это связанные между собой элементы, порождающие новые свойства. Поэтому третий слой можно рассматривать как новые свойства. Далее триаду «свойства –> элементы –> связи» можно повторять, образуя все более сложные понятия, классы, ощущения, функции, системы за счет введения новых слоев сети. Фактически на этом строится «глубокое обучение». Чем больше слоев сети – тем сложнее и абстрактнее понятия, которыми она оперирует. По сути разум, проявляемый нашим мозгом, есть суть сложная функция, подобная устройству окружающего нас мира, модель мира. Мозг – цифровой двойник мира и даже более того, но при наличии у него более высоких абстракций (слоев сети). Как мир усложняется согласно «Всемирной таблице элементов и систем», так и мозг усложняется в понимании (отражении) мира. Однако, мозг может развиваться быстрее и даже обгонять процесс усложнения мира.
Итог:
x y – признаки–свойства, ощущения мира нейронной сетью
z = (5x + 7y - 35<=0) – неравенство, область-поле, свойство
A = (-z - v - w + 3<=0) – выпуклая замкнутая фигура, пересечение свойств, объект, элемент
C = A&НЕ(B) = (-2A + B + 2<=0) – произвольная область, в том числе вогнутая, функция, действия над объектами, отношения, логика, новое свойство
Самостоятельно нарисуйте сеть, которая может решить задачу на теорему Пифагора.
Предостережение!
Нейрон представляют в литературе базисом для построения любых систем также, как наш мозг может конструировать любые сложные представления о мире внутри себя, отражать любые законы окружающего нас мира. (При этом вектор весов связей w представляется как нечто, что меняется медленно в процессе обучения, а x – быстро в зависимости от реакций окружающего мира).
Однако, для универсализации модель Мак-Каллока-Питтса должна дополнительно разрешать соединять входные сигналы рецепторов с весовыми коэффициентами связей. Входной сигнал должен управлять весовым коэффициентом напрямую. Именно такое соединение обеспечит мультипликацию (умножение) сигналов и конструкции типа x2, x3 и тому подобное. Например, для отражения в мозге законов: x2 + y2 = c2, F=m*a. В реальном нейроне, таким образом, есть нечто, что дает возможность влиять сигналу x непосредственно на вес связи w. И этого не хватает в модели М-П.
Не хватает также реализации на нейронах разложения в известные ряды Уолша, Фурье и так далее. Это является ограничением модели Мак-Каллока-Питтса. Поскольку наш мозг составляет такие конструкции, а модель - нет, то это говорит о нашем неполном знании о природе нейрона.
Как же все-таки справляется модель Мак-Каллока-Питтса с нелинейностями?
- Представляя их в виде ломаных прямых линий. При огромном количестве нейронов сети это возможно. Понятие нелинейности образуется уже в следующем слое, если предыдущий слой достаточно велик.
Пример.
Рассмотрим, как настроить нейронную сеть, которая содержит множество слоев нейронов.
Возьмем для примера двухслойную сеть с двумя рецепторами на входе.
|
|
| Рисунок 7.1 – Нейросеть, 2 слоя, 2 рецептора |
Для настройки нейросети используют алгоритм обратного распространения волны (Backpropagation algorithm), в процессе которого будут изменяться веса связей (и значения порогов, которые тоже вынесены как связи) таким образом, чтобы обеспечить целевой уровень сигнала на выходе сети при заданных входных сигналах. То есть, если вход не обеспечивает заданный уровень выходного сигнала, то значения весов каких-то связей надо увеличить, а каких-то уменьшить.
Дано: набор примеров, на которых обучается сеть. Один из примеров показан в таблице 7.1.
Таблица 7.1 – Вариант примера при обучении нейросети (dataset)
| Входные сигналы сети | Выходной сигнал сети | |
| U1 | U2 | U5 (Цель) |
| 0 | 1 | 1 |
| ... | ... | ... |
Старт начальных условий.
Веса связей сети в самом начале генерируются случайным образом. Например:
w13 = 1; w14 = -1; w23 = 0.5; w24 = 2; w3 = 1; P3 = 1; w4 = 1; P4 = 1; w35 = 1.5; w45 = -1; w5 = 1; P5=1.
Алгоритм состоит в повторении на каждой итерации трех действий, формулы для расчета которых имеют вид:
E0 = 0.5*(Цель - uвыход)2
| E0 = (Цель - uвыход)*uвыход*(1 - uвыход) | (1) |
| Ei = w*Ei-1*ui*(1 - ui) | (2) |
| wijновое = wijстарое + h*Ei*ui | (3) |
1. Прямой проход от входа к выходу сети с целью узнать, насколько обеспечен желаемый выход при текущем уровне связей. Разность текущего значения выхода сети (u) с целевым значением (переменная Цель) называется ошибкой сети Е0 (1).
2. Обратный проход последовательно по слоям от выхода ко входу нейросети.
2.1. При обратном проходе на каждой итерации по значению ошибки на выходе слоя вычисляются ошибки на входе слоя Еj(2).
2.2. Коррекция веса wij связей текущего слоя нейронов с целью уменьшить в дальнейшем ошибку данного слоя Еj(3).
Пункты 2.1 и 2.2 повторяются с каждый очередным слоем от конца к началу сети, меняя по пути веса связей нейронов всех слоев.
Описанную итерацию повторяют для каждого примера, на множестве которых (dataset) обучается сеть. В конце множества примеров проверяют, обучилась сеть или нет по значению ошибки сети (п.1). Эти итерации называются эпохой.
Далее эпохи повторяются до тех пор, пока ошибка сети не станет приемлемой или веса связей перестанут менять свои значения.
Расчет состояния сети будем вести по формулам:
S = wi j*ui + wi+1 j*ui+1 + wi+2 j*ui+2 + … ,
то есть
| uj = f(wi j*ui + wi+1 j*ui+1 + wi+2 j*ui+2 + …) | (4) |
| f = 1/(1 + e(-S*L)) | (5) |
Исходное состояние сети изображено на рисунке 7.2.
|
|
| Рисунок 7.2 – Нейросеть с текущим (стартовым) значением настроек и входом сети (0,1) из примера 1 |
Необходимо, чтобы сеть при u1 = 0 и u2 = 1 на выходе дала u5 = 1 (цель).
Примем функцию активации в виде: f = 1/(1 + e(-S*L)). Шаг обучения h = 0.5. Крутизна функции f: L = 1.
Шаг 1.
Осуществляем прямой проход от входа к выходу сети с целью узнать, насколько обеспечен желаемый выход при текущем уровне связей. Разность текущего значения выхода сети с целевым значением называется ошибкой сети (1).
u1 = 0, u2 = 1,
u3 = f(w13*u1 + w23*u2 + w3*P3) = f(1*0 + 0,5*1 + 1*1) = f(1.5) = 0.82
u4 = f(w14*u1 + w24*u2 + w4*P4) = f((-1)*0 + 2*1 + 1*1) = f(3) = 0.95
u5 = f(w35*u3 + w45*u4 + w5*P5) = f(1.5*0.82 + (-1)*0.95 + 1*1) = f(1.22) = 0.78
То есть на выходе сеть дает u5 = 0.78, в то время как должна дать u5 = 1 (цель).
Ошибка сети составляет E0 = 0.5*(Цель - u5)2 = 0.5*(1 - 0.78)2 = 0.024.
Это означает, что сети не хватает мощности сигнала на выходе. Логика изменений состоит в том, чтобы повысить силу возбуждающих связей и понизить силу тормозящих связей при положительных сигналах.
Шаг 2.1.
Вычисляем ошибки на выходах нейронов сети предыдущего слоя.
E0 = Eu5 = (1 - 0.78)*0.78*(1 - 0.78) = 0.037, то есть E0 = (Цель - uвыход)*uвыход*(1 - uвыход)
Eu4 = Eu5*w45*u4*(1 - u4) = 0.037*(-1)*0.95*(1 - 0.95) = -0.00169, то есть Ei = w*Ei-1*ui*(1 - ui)
Eu3 = Eu5*w35*u3*(1 - u3) = 0.037*1.5*0.82*(1 - 0.82) = 0.00834, то есть Ei = w*Ei-1*ui*(1 - ui)
Шаг 2.2.
Меняем веса связей сети в соответствии с вычисленными ошибками.
Сначала на последнем слое:
w45новое = w45старое + h*E0*u4 = -1 + 0.5*0.037*0.95 = -0.988,
то есть wijновое = wijстарое + h*Ei*ui
Из полученного результата ясно, что тормозная связь w45 должна быть ослаблена с (-1) до (-0.988), чтобы позволить сигналу на выходе вырасти.
w35новое = w35старое + h*E0*u3 = 1.5 + 0.5*0.037*0.82 = 1.515
Возбуждающая связь w35 должна быть еще усилена с 1.5 до 1.515, чтобы позволить сигналу на выходе вырасти.
w5новое = w5старое + h*E0*Р5 = 1 + 0.5*0.037*1 = 1.01865
Связь w5, по сути порог нейрона 5, должна быть усилена (порог уменьшен) с 1 до 1.02, чтобы позволить сигналу на выходе вырасти.
Теперь корректируем веса предыдущего слоя.
w24новое = w24старое + h*Eu4*u2 = 2 + 0.5*(-0.00169)*1 = 1.999
w14новое = w14старое + h*Eu4*u1 = -1 + 0.5*(-0.00169)*0 = -1
Связь w14 оставляем без изменения.
w23новое = w23старое + h*Eu3*u2 = 0.5 + 0.5*0.00834*1 = 0.504
Связь w23 должна быть усилена с 0.5 до 0.504, чтобы позволить сигналу на выходе вырасти.
w13новое = w13старое + h*Eu3*u1 = 1 + 0.5*0.00834*0 = 1
Связь w13 оставляем без изменения.
w4новое = w4старое + h*Eu4*P4 = 1 + 0.5*(-0.00169)*1 = 0.991
Связь w4 должна быть ослаблена с 1 до 0.991, чтобы позволить сигналу на выходе вырасти.
w3новое = w3старое + h*Eu3*P3 = 1 + 0.5*0.00834*1 = 1.00417
Связь w3 должна быть усилена с 1 до 1.00417, чтобы позволить сигналу на выходе вырасти.
Шаг 1.
Проверим реакцию сети с измененными весами связей на сигналы:
u1 = 0, u2 = 1,
u3 = f(w13*u1 + w23*u2 + w3*P3) = f(1*0 + 0,504*1 + 1,004*1) = f(1.508) = 0.8188
u4 = f(w14*u1 + w24*u2 + w4*P4) = f((-1)*0 + 1,999*1 + 0,9991*1) = f(2,9983) = 0.952497
u5 = f(w35*u3 + w45*u4 + w5*P5) = f(1.155*0.8188 + (-0.988)*0.9525 + 1.01865*1) = f(1.32379) = 0.7898
То есть сеть на выходе дает u5 = 0.7898, в то время как должна дать u5 = 1 (цель).
Ошибка сети составляет E0 = 0.5*(Цель - u5)2 = 0.5*(1 - 0.7898)2 = 0.022.
По сравнению с предыдущим шагом ошибка сети на выходе уменьшилась, выходной сигнал приблизился к целевому значению. То есть веса коэффициентов были скорректированы в правильном направлении. Однако, следует продолжать итерации, так как ошибка еще не равна нулю.
Очевидно, при малом значении шага расчет может занять довольно много времени. Чем ближе к решению, тем медленнее сеть обучается.
Смысл примененного правила
Правило, которое было применено при обучении нейронной сети (правило изменения весов связей нейронов), называют дельта-правилом: Δw = const*(D - Y)*X.
Смысл дельта-правила состоит в том, что:
- если при входе Х результат Y = 1 совпал с ожиданием цели D = 1, то значение w не меняется;
- если при входе Х результат Y = 1 НЕ совпал с ожиданием D = 0, то значения весов связей, присоединенных к этим входам, УМЕНЬШАЮТСЯ (D - Y)X = (0 - 1)X = -1X так, чтобы ослабить слишком большой входной сигнал Х;
- если при входе Х результат Y = 0 НЕ совпал с ожиданием D = 1, то значения весов связей, присоединенных к этим входам, УВЕЛИЧИВАЮТСЯ (D - Y)X = (1 - 0)X = 1X так, чтобы усилить недостаточный сигнал Х;
- если вход Х = 0, то веса связей не меняются (D - Y)X = (D - Y)*0 = 0, так как сети этот сигнал безразличен.
В целом алгоритм обратной волны обоснован математически следующим.
Если рассмотреть i-тый нейрон сети (рис. 7.3), то его модель выражается:
Si = ∑Xi*wij или Si = ∑Yj*wij
Yi = 1/(1 + e(-Si))
|
|
| Рисунок 7.3 – Состав нейрона и его особые точки (выделено красным) |
При этом функция Y = f(X) такова, что ее производная выражается через саму себя:
dY/dS = Y*(1 - Y)
Ошибка на выходе сети E0 – отклонение выходного сигнала сети Y от желаемого его значения D – составляет:
E0 = ½*∑(Yi - D)2
Требуется E->min за счет изменения вектора весовых коэффициентов связей w.
Алгоритм состоит в следующем.
Следует выяснить чувствительность выхода Y сети по ее входу X, то есть производную. Чувствительность - это то, на сколько можно изменить коэффициенты весов связей w в формуле:
wновое = wстарое + Δw.
Возьмем производную сложной функции от выхода по входу. Поскольку функция сложная и зависит от каскада преобразований, то берем производную как производную сложной функции, проходя ее от конца к началу через все составляющие нейрона (рисунок 7.3).
1. Δai = ∂E/∂Yi = (Yi - D) – находим изменение ошибки ∂E от изменения величины сигнала на выходе ∂Yi нейрона
2. Δbi = ∂E/∂Si = ∂E/∂Yi*∂Yi/∂Si
Так как ∂E/∂Yi = Δai, а dY/dS = Y*(1 - Y), то:
Δbi = ∂E/∂Si = ∂E/∂Yi * ∂Yi/∂Si = Δai*Yi*(1 - Yi) – находим изменение ошибки Е от изменения суммарного сигнала на входе нейрона.
Это ничто иное как выражение ошибки: E0 = (Yi - D) * Yi*(1 - Yi).
3. Δwij = ∂E/∂wij = ∂E/∂Si*∂Si/∂wij
Так как ∂E/∂Si = Δbi, а ∂Si/∂wij =, то
Δwij = ∂E/∂wij = ∂E/∂Si*∂Si/∂wij = Δbi*Yj
или Δwij = E0*Yj – изменение ошибки от изменения веса связи.
Примечание: это выражение дает возможность вычислить wновое = wстарое + Δw для данного слоя нейросети. (3’)
4. Δai = ∂E/∂Yi = ∑ ∂E/∂Si*∂Si/∂Yj =
Так как ∂E/∂Si = Δbi, а ∂Si/∂Yj =, то
Δai = ∂E/∂Yi = ∑ ∂E/∂Si*∂Si/∂Yj = ∑ Δbi*wij
или Δaj = E0*wij - изменение ошибки от изменения значения сигнала на выходе предыдущего слоя j.
После этого пункты 2-3-4-2-3-4-… выполняются для остальных слоев сети от конца к началу.
Пункт 1 выполняется один раз для выходного слоя.
Пункты 2-4 выполняются для всех слоев нейронной сети. Параллельно выполняется пункт 3’, уточняя веса wij связей всех слоев сети.
Схема расчета wij и движения алгоритма от конца к началу сети по ее слоям показаны на рисунке 7.4.
|
|
| Рисунок 7.4 – Схема алгоритма обратной волны |
Занятие 8. Глубокое обучение и архитектура нейросетей
Глубокое обучение - обширная современная область применения теории нейронных сетей.
В 90-е годы в надежде получить серьезные практические результаты, которые бы нашли свое применение в промышленности, количество слоев нейронов в сети попытались резко увеличить.
Отсюда появился и термин – глубокое (многослойное) обучение.
Кроме того, стали применять различные приемы для обработки результатов работы сети после каждого промежуточного слоя. Оригинальные приемы, которые при этом надо использовать, каждый исследователь придумывал сам. Некоторые реализации при этом работали лучше, некоторые - хуже. Все это напоминает действия шамана. Первым стал искать новые архитектуры сетей Ле Кун. Рассмотрим эти идеи на примере распознавания образов. Поэтому рецепторы будут собраны в двухмерную матрицу и каждый слой интернейронов будет соответственно представлять собой двухмерное поле.
Обработка результатов работы отдельного слоя выполняется с целью:
- уменьшить количество нейронов в следующем слое, обобщить информацию, чтобы из начального множества данных в начале сети в ее конце получить концентрированное (небольшое) множество, модель;
- ввести иерархию признаков, формируя все более абстрактные признаки по мере обобщения информации.
Одним из приемов промежуточной обработки была свертка изображения (отсюда термин «сверточные сети»). Каждой отдельной небольшой области исходного изображения предъявлялась небольшая область с конкретным элементом изображения из конструктора (вертикальная полоска, горизонтальная полоска, развилка и т.д.) и вычислялась похожесть этой области на конкретный элемент конструктора. Таких элементов в составе конструктора было несколько (рис.8.1). Изображения фильтров вводятся со стороны в каждый слой сети. Нейрон представляет собой при этом «сравниватель» дошедшего до него со входа сети сигнала и фильтра.
|
|
| Рисунок 8.1 – Элементы конструктора Крижевского (2012 г.) и конструктора Габора (1947 г.) |
Чтобы узнать похожесть двух фрагментов картинок (например, размером 3*3), достаточно было умножить элемент изображения (пиксель) на соответствующий пиксель отдельного шаблона из конструктора, и далее сложить результаты произведений. Перемещаясь заданным шагом по основной картинке, процедура повторялась с каждой новой частью изображения. Это позволяло найти на исходной картинке более или менее похожие элементы конструктора. О чем сообщалось на второй слой сети, который «видел» уже не саму картинку из пикселей изображения, а некоторую «формулу» - где встречаются те или иные типовые логические части изображений. Поскольку из элементов базиса можно, как известно, составить любую картинку, то достаточно было узнать в какой мере и где эти элементы участвуют в составе исходной картинки.
|
|
| Рисунок 8.2 – Пример обработки элементом конструктора (К, ядро 3*3) части исходного изображения S = I*K = 1*1 + 0*0 + 0*1 + 1*0 + 1*1 + 0*0 + 1*1 + 1*0 + 1*1 = 4. Результат обработки – карта I*K обработки изображения К-тым элементом конструктора |
В сущности, сумма произведений – это мера похожести сравниваемых элементов, косинус угла между ними. Если в конструкторе находится базис, то исходная картинка раскладывается как бы по этому базису и превращается в свой спектр. (Элементы конструктора еще называют шаблонами, ортами, фильтрами). Одновременно стоит отметить, что сумма произведений – это основная операция нейрона, поэтому Ле Кун применил ее вполне законно.
На рисунке 8.3 показано исходное входное изображение (лицо), два фильтра Габора, на которые умножается данное изображение и результат свертки изображения лица и фильтров Габора. Видно, что свертка выделяет некоторую информацию, характерную для изображения, уничтожая детали.
|
|
| Рисунок 8.3 – Свертка изображения с помощью фильтров Габора |
После обработки всего изображения первым элементом конструктора и формирования соответствующей первой карты тоже самое производят со вторым элементом, получая вторую карту, и так далее. В результате получается столько карт, сколько элементов находится в составе конструктора. Этап называется convolution (рис.8.4) – свёртка.
|
|
| Рисунок 8.4 – Архитектура многослойной сети для глубокого обучения Ле Куна |
Многократное применение свертки позволяет выделять все более общие признаки конкретного изображения. На изображениях последних слоев нейросети мы можем видеть что-то очень абстрактное, фактически не узнавая исходное изображение, однако это и есть «портрет» понятия в самом общем виде.
|
|
| Рисунок 8.5 – Изображения в различных слоях свёрточной глубокой сети |
Далее проводят операцию пулинга (pooling), выбрав для этого какую-нибудь функцию (сумма, среднее арифметическое, средне взвешенное, максимальное) для преобразования ячеек второго слоя в третий. Такое преобразование производит действие сродни действию активационной функции в нейроне. На рисунке 8.6 показано применение функции «max» для формирования следующего слоя сети. Поле (предыдущий слой) нейронов разбивается на части, в каждой из которых выбирается максимальное значение из значений содержащихся в нем ячеек. Это позволяет:
- провести операцию, напоминающую работу активационной функции в нейроне,
- внести нелинейность в обработку информации,
- сжать количественно слой нейронов, а, значит, создать предпосылки к обобщению информации.
|
|
| Рисунок 8.6 – Применение операции пулинга с активационной функцией «max» к слою нейронной сети |
Рассмотренные выше операции (свёртка, пулинг) многократно повторяются (рис.8.7), оправдывая термин «глубокое обучение». Применяют также слой, реализующий операцию dropout. Эта операция упрощает полученную модель (происходит регуляризация) путем того, что обнуляет часть весов связей, выбранных случайно, и увеличивая пропорционально веса оставшихся.
|
|
| Рисунок 8.7 – Многослойная архитектура глубокой нейронной сети (ReLu означает линейчатый нейрон y = max(0, x)) |
На рисунке 8.8 показан результат опытов по распознаванию цифр на некотором множестве примеров.
Следует признать, что такой подход Ле Куна заслуженно вызвал в 2010-2020 гг. огромный интерес разработчиков к построению промышленных нейронных сетей в области распознавания графических образов. Видно, что существенное разнообразие начертаний символов преодолевается за счет выделения существенных признаков отдельных цифр, которые обнаруживаются там, где они есть, независимо от их местоположения. Честно сказать, такая сеть распознает цифру там, где не всегда даже человек ее опознает со стопроцентной вероятностью.
|
|
| Рисунок 8.8 – Ручное начертание цифр и их распознавание нейронной сетью |
На рисунке 8.9 показаны отклики нейросети в различных слоях. Видно, как постепенно абстрагируется и обобщается распознаваемое изображение.
|
|
| Рисунок 8.9 – Опознавание элементов и изображений во внутренних слоях нейронной сети |
Сеть обучают на множестве примеров, собранных в dataset. Типичный доступный в Интернете датасет ”ImageNet” (рис.8.10) содержит 1 200 000 изображений, разбитых на 1000 различных классов (гриб, баскетбол, кошка, автомобиль и т.п.) по примерно 1000 разных изображений (примеров) в каждом классе. Каждый пример отмечен человеком-экспертом: «что на нем изображено». После обучения сеть ставят в режим экспертизы, предъявляя новые ранее неизвестные ей изображения, которые она должна правильно опознать. На рис.8.10 под изображениями видны надписи, которые обученная сеть выбирает с определенной долей вероятности. Успешность работы сети зависит от ее архитектуры, выбранных функций пулинга, параметров сверток, количества слоев, на чей счет не существует пока никакой теории. Ниже будут приведены характеристики разных нейронных сетей и их эффективность, а также особенности архитектуры.
Методом проб и ошибок различные исследователи формируют свои архитектуры и свои оригинальные приемы формирования нейросетей (например, добавляя аугментацию). Аугментация – процесс обучения сети копиям изображений, которые по сравнению к исходным примерам поворачивались на случайный угол, масштабировались, зеркалировались, смещались и обрезались (видна часть изображения). Сколько поставить слоев, какие параметры принять, какие операции применить, какие фильтры изобрести – решает исследователь.
На запрос «найти похожие изображения» обученная сеть выдает изображения, которые по ее мнению подобны по смыслу предъявленной пользователем эталонной картинке (рис.8.11).
|
|
| Рисунок 8.10 – Множество примеров изображений предметов и сцен, созданных для обучения сетей распознаванию образов, (слева) и их экспертиза (справа) |
|
|
| Рисунок 8.11 – Множество сцен, на которых изображена по мнению нейросети «игра в баскетбол» |
Подробнее Вы можете узнать про данную технологию, посмотрев видео лекции «Сверточные сети», прочитанные в МГУ:
Data mining. Сверточные нейронные сети
Ниже представлены релизы с различными архитектурами сетей.
Алгоритмы глубоких нейросетей сегодня обрели большую популярность, которая во многом обеспечивается продуманностью архитектур. Рассмотрим историю их развития за последние несколько лет. Более глубокий анализ содержится в этой работе.
|
|
| Рисунок 8.11 - Сравнение популярных архитектур по Top-1 one-crop-точности и количеству операций, необходимых для одного прямого прохода. |
LeNet5
В 1994-м была разработана одна из первых свёрточных нейросетей, положившая начало глубокому обучению. Эта пионерская работа Яна Ле Куна (Yann LeCun) после многих успешных итераций, начиная с 1988-го, получила название LeNet5. Архитектура сети показана на рис.8.4.
Архитектура LeNet5 стала фундаментальной для глубокого обучения, особенно с точки зрения распределения свойств изображения по всей картинке. Свёртки с обучаемыми параметрами позволяли с помощью нескольких параметров эффективно извлекать одинаковые свойства из разных мест. В те годы ещё не было видеокарт, способных ускорить процесс обучения, и даже центральные процессоры были медленными. Поэтому ключевым преимуществом архитектуры оказалась возможность сохранять параметры и результаты вычислений, в отличие от использования каждого пикселя в качестве отдельных входных данных для большой многослойной нейросети. В LeNet5 в первом слое пиксели не используются, потому что изображения сильно коррелированы пространственно, так что использование отдельных пикселей в качестве входных свойств не позволит воспользоваться преимуществами этих корреляций.
Особенности LeNet5:
- Свёрточная нейросеть, использующая последовательность из трёх слоёв: слои свёртки (convolution), слои группирования (pooling) и слои нелинейности (non-linearity) –> с момента публикации работы Ле Куна это, пожалуй, одна из главных особенностей глубокого обучения применительно к изображениям.
- Использует свёртку для извлечения пространственных свойств.
- Подвыборка (subsampling) с использованием пространственного усреднения карт.
- Нелинейность в виде гиперболического тангенса или сигмоид.
- Финальный классификатор в виде многослойной нейросети (MLP).
- Разреженная матрица связности между слоями (аугментация) позволяет уменьшить объём вычислений.
Эта нейросеть легла в основу многих последующих архитектур и вдохновила множество исследователей.
Развитие
С 1998-го по 2010-й нейросети пребывали в состоянии инкубации. Большинство людей не замечали их растущих возможностей, хотя многие разработчики постепенно оттачивали алгоритмы. Благодаря расцвету камер мобильных телефонов и удешевлению цифровых фотоаппаратов пользователям становилось доступно всё больше данных для обучения. Заодно росли и вычислительные возможности, процессоры становились мощнее, а видеокарты превратились в основной вычислительный инструмент. Все эти процессы позволяли развиваться и нейросетям, пусть и довольно медленно. Возрастал интерес к задачам, которые можно было решить с помощью нейросетей, и наконец ситуация стала очевидной…
Dan Ciresan Net
В 2010-м Дан Кирешан (Dan Claudiu Ciresan) и Йорген Шмидхубер (Jurgen Schmidhuber) опубликовали одно из первых описаний реализации GPU-нейросетей. Их работа содержала прямую и обратную реализацию 9-слойной нейросети на NVIDIA GTX 280.
AlexNet
В 2012-м Алексей Крижевский опубликовал AlexNet, углублённую и расширенную версию LeNet, которая с большим отрывом победила в сложном соревновании ImageNet.
|
В AlexNet результаты вычислений LeNet масштабированы в гораздо более крупную нейросеть, которая способна изучить намного более сложные объекты и их иерархии. Особенности этого решения:
- Использование блоков линейной ректификации (ReLU) в качестве нелинейностей. ReLu – это линейчатый нейрон, у которого y=max(0,x), см. рис.1.4.б.
- Использование методики отбрасывания для выборочного игнорирования отдельных нейронов в ходе обучения, что позволяет избежать переобучения модели.
- Перекрытие max pooling, что позволяет избежать эффектов усреднения average pooling.
- Использование NVIDIA GTX 580 для ускорения обучения.
К тому времени количество ядер в видеокартах сильно выросло, что позволило примерно в 10 раз сократить время обучения, и в результате стало возможно использовать куда более крупные датасеты и картинки.
Успех AlexNet запустил небольшую революцию, поскольку свёрточные нейросети превратились в рабочую лошадку глубокого обучения — этот термин отныне означал «большие нейросети, способные решать полезные задачи».
Overfeat
В декабре 2013-го лаборатория NYU Яна Ле Куна опубликовала описание Overfeat, разновидности AlexNet. Также в статье описывались обучаемые bounding boxes, и впоследствии вышло много других работ по этой тематике. Многие считают, что лучше научиться сегментировать объекты, а не использовать искусственные bounding boxes.
VGG
В разработанных в Оксфорде VGG-сетях в каждом свёрточном слое впервые применили фильтры 3х3, да ещё и объединили эти слои в последовательности свёрток.
Это противоречит заложенным в LeNet принципам, согласно которым большие свёртки использовались для извлечения одинаковых свойств изображения. Вместо применяемых в AlexNet фильтров 9х9 и 11х11 стали применять гораздо более мелкие фильтры, опасно близкие к свёрткам 1х1, которых старались избежать авторы LeNet, по крайней мере в первых слоях сети. Но большим преимуществом VGG стала находка, что несколько свёрток 3х3, объединённых в последовательность, могут эмулировать более крупные рецептивные поля, например, 5х5 или 7х7. Эти идеи позднее будут использованы в архитектурах Inception и ResNet.
Сети VGG для представления сложных свойств используют многочисленные свёрточные слои 3x3. Обратите внимание на блоки 3, 4 и 5 в VGG-E: для извлечения более сложных свойств и их комбинирования применяются последовательности 256?256 и 512?512 фильтров 3?3. Это равносильно большим свёрточным классификаторам 512х512 с тремя слоями! Это даёт нам огромное количество параметров и прекрасные способности к обучению. Но учить такие сети было сложно, приходилось разбивать их на более мелкие, добавляя слои один за другим. Причина заключалась в отсутствии эффективных способов регуляризации моделей или каких-то методов ограничения большого пространства поиска, которому способствует множество параметров. VGG во многих слоях используют большое количество свойств, поэтому обучение требовало больших вычислительных затрат. Снизить нагрузку можно, уменьшив количество свойств, как это сделано в bottleneck-слоях архитектуры Inception.
|
Network-in-network
В основе архитектуры Network-in-network (NiN) лежит простая идея: использование свёрток 1x1 для увеличения комбинаторности свойств в свёрточных слоях.
В NiN после каждой свёртки применяются пространственные MLP-слои, чтобы лучше скомбинировать свойства перед подачей в следующий слой. Может показаться, что использование свёрток 1х1 противоречит исходным принципам LeNet, но на самом деле это позволяет комбинировать свойства лучше, чем просто набивая больше свёрточных слоёв. Этот подход отличается от использования голых пикселей в качестве входных данных для следующего слоя. В данном случае свёртки 1х1 применяются для пространственного комбинирования свойств после свёртки в рамках карт свойств, так что можно использовать гораздо меньше параметров, которые являются общими для всех пикселей этих свойств!
|
MLP позволяют сильно повысить эффективность отдельных свёрточных слоёв посредством их комбинирования в более сложные группы. Эта идея позднее была использована в других архитектурах, таких как ResNet, Inception и их вариантах.
GoogLeNet и Inception
Кристиан Жегеди (Christian Szegedy) из Google озаботился снижением объёма вычислений в глубоких нейросетях и в результате создал GoogLeNet — первую архитектуру Inception.
К осени 2014-го модели глубокого обучения стали очень полезны в категоризировании содержимого изображений и кадров из видео. Многие скептики признали пользу глубокого обучения и нейросетей, а интернет-гиганты, в том числе Google, сильно заинтересовались развёртыванием на своих серверных мощностях эффективных и крупных сетей.
Кристиан искал пути уменьшения вычислительной нагрузки в нейросетях, добиваясь высочайшей производительности (например, в ImageNet). Или сохраняя объём вычислений, но всё равно при этом повышая производительность.
В результате команда создала модуль Inception.
|
На первый взгляд, это параллельная комбинация свёрточных фильтров 1х1, 3х3 и 5х5. Но изюминка заключалась в использовании свёрточных блоков 1х1 (NiN) для уменьшения количества свойств перед подачей в «дорогие» параллельные блоки. Обычно эту часть называют bottleneck, подробнее она описывается в следующей главе.
В GoogLeNet в качестве начального слоя применяется stem без Inception-модулей, а также используется average pooling и softmax-классификатор, аналогичный NiN. Этот классификатор выполняет крайне мало операций по сравнению с AlexNet и VGG. Это также помогло создать очень эффективную архитектуру нейросети.
Bottleneck-слой
Этот слой уменьшает количество свойств (а значит и операций) в каждом слое, так что скорость получения результата можно сохранить на высоком уровне. Прежде чем передавать данные в «дорогие» свёрточные модули, количество свойств уменьшается, скажем, в 4 раза. Это сильно сокращает объём вычислений, что и обеспечило архитектуре популярность.
Пусть у нас 256 свойств на входе и 256 на выходе, и пусть Inception-слой выполняет только свёртки 3х3. Получаем 256х256х3х3 свёрток (589 000 операций умножения с накоплением, то есть MAC-операций). Это может выходить за рамки наших требований к скорости вычислений, допустим, чтобы слой обрабатывался за 0,5 миллисекунды на Google Server. Тогда уменьшим количество свойств для свёртывания до 64 (256/4). В этом случае сначала выполним свёртку 1х1 256 -> 64, затем ещё 64 свёрток во всех Inception-ветках, а потом снова применим свёртку 1x1 из 64 -> 256 свойств. Количество операций:
- 256?64 ? 1?1 = 16 000
- 64?64 ? 3?3 = 36 000
- 64?256 ? 1?1 = 16 000
Всего около 70 000, снизили количество операций почти в 10 раз! Но при этом мы не потеряли обобщённости в этом слое. Bottleneck-слои продемонстрировали превосходную производительность на датасете ImageNet, и стали применяться в более поздних архитектурах, таких как ResNet. Причина их успеха в том, что входные свойства коррелированы, а значит можно избавиться от избыточности, правильно комбинируя свойства со свёртками 1х1. А после свёртывания с меньшим количеством свойств можно на следующем слое опять развернуть их в значимую комбинацию.
Inception V3 (и V2)
Кристиан и его команда оказались очень эффективными исследователями. В феврале 2015-го в качестве второй версии Inception была представлена архитектура Batch-normalized Inception. Пакетная нормализация (batch-normalization) вычисляет среднее и среднеквадратичное отклонение всех карт распределения свойств в выходном слое и нормализует их отклики с этими значениями. Это соответствует «отбеливанию» данных, то есть отклики всех нейронных карт лежат в одном диапазоне и с нулевым средним. Такой подход облегчает обучение, потому что последующий слой не обязан запоминать смещения (offsets) входных данных и может заниматься только поиском лучших комбинаций свойств.
В декабре 2015-го вышла новая версия модулей Inception и соответствующей архитектуры. В авторской статье лучше объясняется оригинальная архитектура GoogLeNet, там гораздо подробнее рассказано о принятых решениях. Основные идеи:
- Максимизация потока информации в сети за счёт аккуратного баланса между её глубиной и шириной. Перед каждым pooling-ом увеличиваются карты свойств.
- С увеличением глубины также систематически увеличивается количество свойств или ширина слоя.
- Ширина каждого слоя увеличивается ради увеличения комбинации свойств перед следующим слоем.
- По мере возможности используются только свёртки 3x3. Учитывая, что фильтры 5x5 и 7x7 можно декомпозировать с помощью нескольких 3x3
|
Последняя картинка показывает, как выглядит новый Inception-модуль.
- Фильтры также можно декомпозировать с помощью сглаженных свёрток в более сложные модули:
|
- Inception-модули могут с помощью pooling-а в ходе Inception-вычислений уменьшать размер данных. Это аналогично выполнению свёртки со страйдами параллельно с простым pooling-слоем:
|
В качестве финального классификатора Inception использует pooling-слой с softmax.
ResNet
В декабре 2015-го, примерно в то же время, как была представлена архитектура Inception v3, произошла революция — опубликовали ResNet. В ней заложены простые идеи: подаём выходные данные двух успешных свёрточных слоёв И обходим входные данные для следующего слоя.
|
Такие идеи уже предлагались, например, здесь. Но в данном случае авторы обходят ДВА слоя и применяют подход в больших масштабах. Обход одного слоя не даёт особой выгоды, а обход двух — ключевая находка. Это можно рассматривать как маленький классификатор, как сеть-в-сети!
Также это был первый в истории пример обучения сети из нескольких сотен, даже тысячи слоёв. В многослойной ResNet применили bottleneck-слой, аналогичный тому, что применяется в Inception:
|
Этот слой уменьшает количество свойств в каждом слое, сначала используя свёртку 1х1 с меньшим выходом (обычно четверть от входа), затем идёт слой 3х3, а потом опять свёртка 1х1 в большее количество свойств. Как и в случае с Inception-модулями, это позволяет экономить вычислительные ресурсы, сохраняя богатство комбинаций свойств. Сравните с более сложными и менее очевидными stem-ами в Inception V3 и V4.
В качестве финального классификатора в ResNet используется pooling-слой с softmax. Каждый день появляются дополнительные сведения об архитектуре ResNet:
- Её можно рассматривать как систему одновременно параллельных и последовательных модулей: во многих модулях inout-сигнал приходит параллельно, а выходные сигналы каждого модуля соединяются последовательно.
- ResNet можно рассматривать как несколько ансамблей параллельных или последовательных модулей.
- Выяснилось, что ResNet обычно оперирует блоками относительно небольшой глубины в 20-30 слоёв, работающих параллельно, а не прогоняя последовательно по всей длине сети.
- Поскольку выходной сигнал возвращается назад и подаётся как входной, как это делается в RNN, ResNet можно считать улучшенной правдоподобной моделью коры головного мозга.
Inception V4
Снова отличились Кристиан и его команда, выпустившие новую версию Inception. Inception-модуль, идущий после stem, такой же, как в Inception V3:
|
При этом Inception-модуль скомбинирован с ResNet-модулем:
|
Эта архитектура получилась сложнее, менее элегантной, а также наполненной малопрозрачными эвристическими решениями. Трудно понять, почему авторы приняли те или иные решения, и столь же трудно дать им какую-то оценку.
Поэтому приз за чистую и простую нейросеть, лёгкую в понимании и модифицировании, переходит к ResNet.
SqueezeNet
SqueezeNet опубликовали недавно. Это переделка на новый лад многих концепций из ResNet и Inception. Авторы продемонстрировали, что улучшение архитектуры позволяет уменьшить размеры сетей и количество параметров без сложных алгоритмов сжатия.
ENet
Все особенности недавних архитектур скомбинированы в очень эффективную и компактную сеть, использующую совсем мало параметров и вычислительных мощностей, но при этом дающую превосходные результаты. Архитектура получила название ENet, её разработал Адам Пазке (Adam Paszke). К примеру, мы использовали её для очень точной маркировки объектов на экране и парсинга сцен. Несколько примеров работы Enet. Эти видео не имеют отношения к обучающему датасету.
Здесь можно найти технические подробности ENet. Это сеть на основе кодировщика и декодера. Кодировщик построен по обычной схеме CNN для категоризации, а декодер представляет собой сеть с повышением дискретизации (upsampling netowrk), предназначенную для сегментирования посредством распространения категорий обратно в изображение исходного размера. Для сегментации изображений использовались только нейросети, никаких других алгоритмов.
|
Как видите, ENet имеет наивысшую удельную точность по сравнению со всеми остальными нейросетями.
ENet создавалась из расчёта, чтобы с самого начала использовать как можно меньше ресурсов. В результате кодировщик и декодер вместе занимают всего 0,7 Мб с точностью fp16. И при таком крохотном размере ENet по точности сегментирования не уступает или превосходит прочие чисто нейросетевые решения.
Анализ модулей
Опубликовали систематическую оценку CNN-модулей. Оказалось, что выгодно:
- Использовать нелинейность ELU без пакетной нормализации (batchnorm) или ReLU с нормализацией.
- Применять выученную трансформацию цветового пространства RGB.
- Использовать политику линейного ухудшения скорости обучения (linear learning rate decay policy).
- Использовать сумму среднего и максимального pooling-слоя.
- Использовать мини-пакет размером 128 или 256. Если для конкретной видеокарты это слишком много, то рекомендуется уменьшить скорость обучения пропорционально размеру пакета.
- Использовать полносвязные слои в качестве свёрточных и усреднять прогнозы для выдачи финального решения.
- Если требуется увеличить размер обучающего датасета, то следует удостовериться, что плато в обучении не достигнуто. Чистота данных важнее размера.
- Если невозможно увеличить размер входного изображения, следует уменьшать страйд в последующих слоях, эффект будет примерно таким же.
- Если сеть обладает сложной и высоко оптимизированной архитектурой, как в GoogLeNet, то модифицировать её следует с осторожностью.
Xception
Xception привнесла в Inception-модуль более простую и элегантную архитектуру, которая не менее эффективна, чем ResNet и Inception V4. Вот как выглядит Xception-модуль:
|
Эта сеть понравится кому угодно благодаря простоте и элегантности своей архитектуры.
|
Она содержит 36 этапов свёртки, и в этом схожа с ResNet-34. При этом модель и код просты, как в ResNet, и гораздо приятнее, чем в Inception V4.
Torch7-реализация этой сети доступна здесь, а реализация на Keras/TF — здесь. Любопытно, что авторы недавней архитектуры Xception тоже вдохновлялись работой над отделяемыми (separable) свёрточными фильтрами.
MobileNets
Новая архитектура MobileNets вышла в апреле 2017-го. Для уменьшения количества параметров в ней используются отделяемые свёртки, такие же, как в Xception. Ещё в работе утверждается, что авторы смогли сильно уменьшить количество параметров: примерно вдвое в случае с FaceNet. Полная архитектура модели:
|
После тестирования этой сети на реальной задаче было обнаружено, что она работает крайне медленно на пакете из 1 (batch of 1) на видеокарте Titan Xp. Для сравнения длительность вывода для одного изображения:
- resnet18: 0,002871
- alexnet: 0,001003
- vgg16: 0,001698
- squeezenet: 0,002725
- mobilenet: 0,033251
Другие примечательные архитектуры
FractalNet использует рекурсивную архитектуру, которая пока не тестировалась на ImageNet и является производным или более общим вариантом ResNet.
Будущее
Разработка архитектур нейросетей имеет первостепенную важность для развития глубокого обучения. Для тех, кто будет заниматься сетями, рекомендуем прочитать и обдумать работы, приведённые здесь.
Интересно, почему мы должны тратить столько времени на разработку архитектур, и почему вместо этого не используем данные, которые подскажут нам, что именно применять и как объединять модули? Заманчивая возможность, но работы над этим пока ещё ведутся. Здесь есть некоторые начальные результаты.
Кроме того, мы разговаривали только об архитектурах для компьютерного зрения. В других сферах разработки тоже ведутся, и было бы интересно изучить эволюцию по другим направлениям. Если вас интересует сравнение работы нейросетей и вычислительной производительности, то имеет смысл посмотреть еще одну нашу недавнюю работу.
В публикации https://www.pvsm.ru/algoritmy/70356 проведено сравнение результатов применения разных методов искусственного интеллекта для распознавания лиц.
Занятие 9. Примеры использования нейросетей
Пример 1. Программисты и разработчики компьютерных игр не в состоянии задать все возможные поведения персонажей игры во всех ситуациях. Достаточно использование нейросети, имитирующей поведение каждого персонажа, которую следует обучить на нескольких примерах для того, чтобы персонаж вел себя естественно на новых примерах.
Таблица 9.1 – Пример задания вариантов поведения персонажа компьютерной игры (кодирование выхода сети: 1 – атаковать, 2 – убегать, 3 – прятаться, 4 – уклониться)
| Входные сигналы нейросети | Выходные сигналы нейросети | |||
| Здоровье | Нож | Пистолет | Враг | Поведение |
| 2 | 0 | 0 | 0 | 3 |
| 2 | 1 | 0 | 2 | 4 |
| 1 | 0 | 1 | 1 | 4 |
| 1 | 1 | 1 | 2 | 2 |
| … | … | … | … | … |
Понятно, что примеров должно быть достаточно для построения корректной модели.
Пример 2. Научить сеть арифметическим действиям
Таблица 9.2 – Пример задания для нейронной сети
| Вход сети «a» | Вход сети «b» | Выход сети «с», с=a+b |
| 2 | 3 | 5 |
| 1 | 2 | 3 |
| 1 | 1 | 2 |
| … | … | … |
Сеть обучают на нескольких (не всех) примерах. Затем запрашивают результат на незнакомом примере.
Пример 3. Выявление лжи
С помощью детектора лжи снимают с человека показания, задавая ему вопросы и одновременно регистрируя ответы и состояние 7 параметров кожи. Вопросы (примеры сети) заранее задают такие, на которые человек не будет лгать или будет точно лгать. Сеть обучают на этих достоверных примерах.
Далее, когда сеть настроена, задают интересующие вопросы. Сеть отличает лживые ответы от правдивых. Этим же способом ловят хакеров в Интернете.
Пример 4. Выявление закономерностей изменения валютного курса
Сеть обучают имеющимися большими выборками курса валюты, параллельно давая ей, например, значения солнечной активности или фазы Луны. После обучения сеть может предсказывать курс валюты на завтра по задаваемому ей значению солнечной активности или фазы Луны. Анализ полученных сетью уравнений позволяет определить по величине коэффициентов, влияет ли Солнце или Луна на курс валюты.
Пример 5. Говорящая машина (машина Бриндли)
Сеть обучали 10 000 английских слов, вводя в качестве примеров фразы из 3 слов. Из всех фраз 100 000 фраз имели смысл. На входе сети – 10 000 рецепторов (один рецептор – одно слово).
На экзамене сети задавали два слова, по которым она вспоминала такое третье слово, что фраза имела смысл.
Пример 6. Симметрия изображений
Сети показывали 64 изображения и указывали, на каких изображениях есть симметрия.
На экзамене на новых примерах сеть правильно опознавала симметричные изображения.
Пример 7. Медицина
Сети показывают кардиограммы пациентов с одновременным указанием на наличие у них конкретного заболевания.
Сеть научилась анализировать кардиограммы и ставить предварительные диагнозы.
Пример 8. Машинный перевод
10.07.22 Meta выложила в открытый доступ модель NLLB-200 для перевода текста на 200 языков. Проект «No Language Left Behind» является частью планов Meta по поддержке редко используемых языков и разработке универсального переводчика. Он будет использовать NLLB-200 для улучшения перевода в Facebook, Instagram и, в конечном итоге, в метавселенной.
Подробнее о модели
NLLB-200 — это единая многоязычная модель машинного перевода, которая может переводить на 200 языков с более точными результатами, чем известные на сегодня методы. Модель не требуется сначала преобразовывать текстовый язык в английский, как того требуют другие методы.
Система поддерживает больше языков, чем Google Translate (113) и Microsoft Translator (110). Она переводит менее распространенные языки, такие как лаосский и камба, и 55 африканских языков с «высокоточными результатами». По сравнению с предыдущими моделями ИИ NLLB-200 улучшает качество перевода в среднем на 44%. Точность перевода для некоторых африканских и индийских языков улучшилась на 70%.
Meta выложила исходный код NLLB-200 в открытый доступ, чтобы другие могли использовать или улучшать программное обеспечение.
Пример 9. Google Imagen: генерация фотореалистичных изображений по описанию
Google представила Imagen — модель, трансформирующую текстовое описание в изображение c разрешением 1024?1024 пикселей. Imagen превзошла OpenAI DALL-E 2 по степени реалистичности изображений.
Imagen является комбинацией языковых моделей-трансформеров, используемых для обработки текстового описания, и диффузных моделей для генерации изображений с последовательным улучшением разрешения. Модель была обучена на датасете LAION-400M, содержащем более 400 миллионов пар изображение-текст, взятых из Интернета.
|
Google протестировала Imagen в сравнении с DALL-E 2 с помощью оценок тестировщиков. По итогам этого теста большинство положительных оценок получила модель Google. Помимо этого, Imagen достигла нового state-of-the-art значения FID 7,27 в датасете COCO, хотя не обучалась на изображениях из этого датасета.
В дополнение к Imagen Google представила комплексных бенчмарк text-to-speech моделей DrawBench. На текущий момент компания решила не выпускать модель в открытый доступ, поскольку она подвержена предвзятости данных из обучающего датасета. Посмотреть примеры сгенерированных изображений можно по ссылке.
Пример 10. Генеративное искусство, нейросеть Botto
В последние годы в самых разных отраслях все большее внимание уделяется так называемому генеративному искусственному интеллекту. Это методы машинного обучения, которые могут изучать имеющиеся объекты и использовать полученные знания для получения нового контента: текста, звуков, изображений — и для решения прочих задач.
В проектах использованы технологии генерации изображений и видео на основе заданного текста, алгоритмы распознавания лиц, технологии 3D-печати. Использованы известные нейросети StyleGAN2 и CLIP. Нейросеть Botto была создана международной группой разработчиков и художников.
На примере искусства от Botto видны особенности художника с искусственным интеллектом. Как отмечают его разработчики, во-первых, у него есть серьезные преимущества перед коллегами-людьми. Он может очень быстро изучить историю живописи, анализируя и каталогизируя ее и запоминая все, что он когда-либо видел. Там, где художник-человек должен работать над холстом в течение нескольких дней, месяцев или даже лет, ИИ может создать свои работы за считанные минуты. Конечно, такое искусство является скорее подражанием, чем самостоятельным произведением, но то же самое можно сказать и о подавляющем большинстве художников-людей.
Алгоритм этот состоит в следующем. В начале Botto генерирует случайную последовательность слов и предложений, которую передает в обученную на произведениях искусства нейросеть, а обратно получает изображение. Другая программа определяет, насколько близок этот результат к представлению исходной последовательности слов, и заставляет нейросеть настраивать параметры созданного изображения до тех пор, пока оно не наберет определенный балл. После создания окончательного изображения программа генерирует уже название картины: случайные комбинации из двух слов загружаются в программу до тех пор, пока она не найдет ту, которая, по ее мнению, хорошо согласуется с содержанием изображения.
Из 300 начальных запросов в день Botto создает 300 изображений, которые затем передаются на оценку членам сообщества Botto, голосующим за представленные им произведения, и каждую неделю победитель продается с аукциона на платформе SuperRare.
При этом оценки людей, выставленные при голосовании, также используются для обучения ИИ. Botto извлекает уроки из всей этой обратной связи. Он ищет закономерности в том, что нравится сообществу, и адаптирует свое искусство на основе полученных результатов.
|
Подобные примеры привели разработчиков к построению нового типа компьютерной памяти, более соответствующего человеческой памяти: гетероассоциативной, автоассоциативной, интерполятивной, двунаправленной ассоциативной.
Гетероассоциативная память – если набор входных сигналов близок какому-то из выученных сетью наборов, то на выходе сети появлялся соответствующий этому набору сигнал. Сеть вспоминала ассоциацию. xвх ≈ xi -> yвых ≈ yi.
Автоассоциативная память – сеть восстанавливала полный вектор входных сигналов по его части (например, восстановление всего лица по его части).
Интерполятивная память – если x = xi + d, то f(x) = f(xi + d) = yi + e. Фактически память имитировала процесс индукции.
Двунаправленная ассоциативная память – ассоциативная память, которая работала в обе стороны, от входа к выходу и от выхода ко входу.
Занятие 10. Биология нейрона, нейронной сети и нервной деятельности
Часть 10.1 Явление осмоса
Сок по дереву вверх гонит сила осмотического давления. Осмос - сила самопроизвольного проникновения растворителя (воды) в раствор (вода с сахаром), отделенного от него перепонкой (пленкой, полупроницаемой мембраной), через которую проходит растворитель, но не проходит растворенное вещество. Разность давлений по обе стороны мембраны называется осмотическим давлением. Явление осмоса чрезвычайно разнообразно и во многом определяется природой мембраны и компонентов раствора. Примерами перепонок в природе являются - кожа лягушки, мочевой пузырь, глина. Мембрана характеризуется проведением различных веществ через себя в различные стороны с различной способностью.
Поясним. Внутрь мешочка из мембраны в качестве границы нальем раствор NaCl в H2O. Снаружи налита просто вода.
Смысл здесь в том, что нейтральная молекула NaCl в водной среде распадается на анион Na+ (положительно заряженный ион) и катион Cl- (отрицательно заряженный ион) – так их растаскивает вода, молекулы которой являются диполями (слабыми магнитами). Например, молекула NaCl распадается на крупный катион Cl- и меньший по размеру анион Na+. Если дырки в мембране таковы, что по размеру одни частицы проходят сквозь нее, а другие – нет, то возникает односторонняя проводимость.
Согласно фундаментальному явлению диффузии эти частицы молекулы беспорядочно двигаются, проскакивая через отверстия мембраны, однако не все, а только мелкие Na+. Частицы Cl- через мембрану не проходят, слишком велики. Происходит частичный переход растворимого вещества в среду чистого растворителя из замкнутого мембраной пространства.
Далее в ход идут электрические свойства частиц. Положительно заряженная частица Na+, пройдя через отверстия мембраны на волю, отойти далеко от отрицательно заряженных частиц Cl- не может, ее держат силы притяжения. Частицы, конечно, все время двигаются, однако, возникает динамическое равновесие. Положительно заряженные частицы снаружи мембраны и отрицательно заряженные частицы с ее внутренней стороны образуют природную разность потенциалов, возникающую спонтанно на любой мембранной поверхности, называемую потенциалом Нернста (-80 mB). Заметим, что другие анионы и катионы подойти к этой границе сред не могут, их отталкивают те, которые уже собрались в этот слой, поэтому потенциал Нернста стабилен по величине, устойчив, наблюдается у любого живого организма. Именно потенциал Нернста является первопричиной нервной проводимости сигналов по поверхности клеток.
|
|
| Рисунок 10.1 - Простейший осмометр: А - сосуд с растворителем, Б - трубка с раствором, В - полупроницаемая пленка (мембрана), Г - шкала для измерения разности уровней h. Снаружи мембраны в сосуде – чистый растворитель, внутри мембраны – раствор вещества в растворителе |
Представим, что сосуд с двумя горлами для залива раствора разделен мембраной M (рис. 10.2). В каждую часть сосуда зальем растворы, отличающиеся только концентрацией. Поскольку мольные доли растворителя по обе стороны мембраны не совпадают, то стремление их к выравниванию приведет к переходу части растворителя в ту часть сосуда, где концентрация растворенного вещества больше. Увеличение количества растворителя эквивалентно возрастанию давления, и если мембрана способна к деформации, она изогнется в сторону с меньшей концентрацией растворенного вещества (рис. 10.2 а).
|
|
| Рисунок 10.2 - Схема разности осмотических давлений при χ1 < χ2 при эластичной (а) и жесткой (б) мембранах |
Если мембрана жесткая, то в отсеке с большей концентрацией количество растворителя будет возрастать до тех пор, пока гидростатическое давление h (рис. 10.2 б) не станет равным осмотическому давлению и не прекратит осмос.
Осмотическое давление π – внутреннее давление растворенного вещества, численно равное тому внешнему давлению, которое нужно приложить, чтобы прекратить осмос; оно зависит от температуры и концентрации.
Эту зависимость Вант-Гофф уподобил поведению идеального газа:
π · V = R · T
По Вант-Гоффу осмотическое давление раствора численно равно тому газовому давлению, которое имело бы растворенное вещество, будучи переведенным в газообразное состояние в том же объеме и при той же температуре. Поскольку объем (разбавление) обратно пропорционален концентрации, то закон Вант-Гоффа можно записать в виде:
π = C · R · T
Влияние параметров на процесс обратного осмоса
Давление. Основным фактором, оказывающим влияние на процесс обратного осмоса и ультрафильтрации, является рабочее давление. С увеличением давления увеличивается эффективная движущая сила процесса и, соответственно, возрастает величина проницаемости мембраны. В тех случаях, когда мембрана не изменяет своей структуры под действием давления, проницаемость воды линейно возрастает с увеличением эффективной движущей силы, и поскольку проницаемость растворенного вещества мала по сравнению с проницаемости воды. Общая проницаемость хорошо описывается уравнением:
G = A(P - Δπ), (10.1)
где G – проницаемость воды;
A – константа для системы мембрана - раствор при определенных внешних условиях;
Δπ – разность осмотических давлений растворов по обе стороны мембраны.
Однако при повышенных давлениях реальные полимерные мембраны не сохраняют свою первоначальную структуру и уплотняются, что отражается на величине константы А в уравнении 10.1. В связи с этим, начиная с некоторой величины рабочего давления, проницаемость снижается и при определенных давлениях достигает максимума. При дальнейшем увеличении давления проницаемость снижается.
Сходный характер носит зависимость селективности разделения от давления.
Селективность в области малых давлений линейно возрастает с увеличением давления, затем скорость возрастания снижается и селективность достигает максимальной величины, определяемой типом мембраны и природой растворенного вещества. Такой характер зависимости обусловлен тем, что в области невысоких давлений с увеличением движущей силы возрастает лишь поток воды через мембрану, в то время как поток растворенного вещества практически не меняется. То, что селективность остается постоянной даже после достижения максимума проницаемости, объясняется снижением потока растворенного вещества через мембрану при значительном ее уплотнении.
Температура. Влияние температуры раствора на процесс имеет сложный характер. Увеличение температуры уменьшает вязкость и плотность раствора и одновременно увеличивает его осмотическое давление. Если уменьшение вязкости и плотности приводит к увеличению проницаемости, то увеличение осмотического давления снижает движущую силу и уменьшает проницаемость. Степень влияния тех или иных факторов зависит от природы растворенного вещества и концентрации раствора. Исследования, проведенные на чистой воде и водных растворах NaCl, показали, что в диапазоне температур 100 – 400 С проницаемость и селективность возрастают. Причем влияние температуры на селективность становиться все боле заметным с повышением концентрации. Влияние температуры на проницаемость при разделении растворов невысокой концентрации практически полностью определяется изменением вязкости раствора и хорошо коррелируется соотношением:
G · μ = const, (10.2)
где G – проницаемость растворителя;
μ – вязкость раствора.
Для более концентрированных растворов величина G*μ уменьшается с увеличением температуры.
Влияние температуры на производительность мембранных установок практически одинаково как для чистой воды, так и для разбавленного щелока, если его осмотическое давление меньше приложенного на 70%. Это объясняется тем, что осмотическое давление разбавленного щелока почти не зависит от температуры в интервале 100 – 350 С. Условно проницаемость мембраны при температуре 250 принята за 100. Эту зависимость можно представить уравнением:
G/G25 = 30 + 2.8 · t = const. (10.3)
Во многих случаях повышение температуры способствует размыванию осажденного на мембране слоя, поэтому в пределах термостойкости мембран использование повышенных температур может быть оправдано.
Концентрация раствора. Увеличение концентрации раствора приводит к уменьшению движущей силы процесса ΔP = (P - Δπ) , увеличению вязкости и плотности раствора, что снижает величину проницаемости.
Для учета изменения проницаемости в связи с изменением концентрации предложено следующее эмпирическое соотношение:
G = ΔP · ρ/μ · k1/(k2 + xn), (10.4)
k1, k2, n – константы, характеризующие конкретную систему мембрана – раствор;
х – концентрация исходного раствора;
ρ – плотность раствора;
μ – вязкость раствора.
Зависимость селективности от концентрации носит более сложный характер. В случае разделения растворов невысокой концентрации селективность существенно не меняется с изменением концентрации, а падение концентрации можно считать линейным.
Проницаемость более плотных мембран ниже, чем мембран средней плотности. Это происходит вследствие загрязнения мембран осаждающимся слоем некоторых компонентов раствора (в различной степени для различных стоков). Происходит проникновение инородных веществ в структуру полупроницаемой мембраны, а образовавшийся слой, работающий как вторая мембрана, изменяет параметры процесса.
Часть 10.2 Мембранная теория
Внутри клетки имеется много свободных ионов например К+, а снаружи таких ионов нет или их гораздо меньше. Клеточная мембрана пропускает только эти ионы и не пропускает анионы. Тогда ионы К+ начнут двигаться наружу, туда, где их меньше. Вместе с ними будет выноситься и положительный заряд. Внутрь будет проходить мало ионов, т.к. снаружи их мало. В результате на мембране будет возникать разность потенциалов. Эта разность будет тормозить движение ионов К+ наружу и увеличивать их поток внутрь. Когда эти потоки сравняются на мембране установится постоянная разность потенциалов (потенциал покоя). Его величина описывается формулой Нернста.
|
|
| Рисунок 10.3 - Схема работы натрий-калиевого насоса: а - активные центры захватили ион калия снаружи и ион натрия внутри клетки; б - белковая молекула, захватившая ионы, повернулась на 180° за счет энергии АТФ и освободила захваченные ионы, при этом калий попал внутрь клетки, а ион натрия был выброшен наружу в - молекула вновь повернулась на 180° и готова к захвату новых ионов. |
|
|
| Рисунок 10.4 – Реальный состав и структура кальциевого канала |
Устройство клеточной мембраны: состоит из жироподобного вещества (липиды), толщиной в 2 молекулы со встроенным множеством белковых молекул. (Жироподобные вещества гидрофобны, поэтому молекулы липидов встают «торчком» к границе сред. Подобные пленки мы наблюдаем в луже, в которую капнули масло, - масляная пленка расползается по поверхности воды толщиной ровно в одну молекулу).
Эти молекулы - ионные каналы (насосы) - пропускают одни вещества и не пропускают другие. Разные белковые вставки обеспечивают действие различных "фильтров". Со временем ионные каналы и образуются, и разрушаются, происходит их непрерывная регенерация. Синтезируют каналы рибосомы под управлением РНК. Ионные каналы вероятностные - в один момент времени они могут перевернуться (сработать) и пропустить вещество в клетку, а могут этого и не сделать. Таким образом природа защищается от ударных нагрузок.
Диффузия ионов в жидкостях осуществляет диффузию зарядов. NaCl - раствор соли в воде. Идет расслаивание ионов - возникает потенциал Нернста. У клетки возникает поверхностный заряд (-80 mB).
Если мембрану возбудить внешним источником (20 mB), то эта мембрана становится более проницаемой для ионов Na (в 20 раз больше). Ионов Na существенно больше в среде - возникает натриевый ток и клетка перезаряжается (заряд вместо отрицательно становится положительным) и находится в таком заряженном состоянии. Но в связи с тем, что Na становится больше, то передергивать Na из среды клетка перестает, процесс останавливается в точке равновесия.
Увеличение потенциала приводит к инициации такого же процесса со стороны калия. Однако, этот процесс идет встречно и медленнее, так как это другое вещество (проводимость по натрию и калию отличается в 23 раза). А это значит, что через некоторое время потенциал на мембране приходит обратно в норму. Импульс состоялся. Длина импульса τ = 4мс (ответ клетки на внешнее раздражение) обусловлено химическими параметрами веществ NaCl и KCl.
|
|
| Рисунок 10.5 - Возникновение разности потенциалов на полупроницаемой мембране: А - раствор с низкой концентрацией ионов (наружная среда), Б - полупроницаемая мембрана, пропускающая положительные ионы калин, но не пропускающая анионы, В - раствор с высокой концентрацией ионов внутри клетки, а - Исходное состояние до возникновения разности потенциалов: внутри ионов калия (черные точки) много, снаружи (раствор А) - мало, но и там, и там заряды ионов калия компенсируются отрицательными зарядами анионов, б - Конечное состояние динамического равновесия: часть ионов калия проникла через полупроницаемую мембрану, снаружи положительных зарядов стало больше, чем отрицательных, внутри - наоборот. Анионы тянут "убежавшие" ионы калия назад, в результате потоки ионов калия через мембрану в ту и в другую сторону становятся равными. Возник потенциал Нернста. |
Часть 3, 4. Проницаемость мембраны. Теория "местных токов". Распространение возбуждения по нервному волокну
|
|
| Рисунок 10.6 - Зависимость калиевой (а) и натриевой (б) проводимостей клеточной мембраны от времени и от величины деполяризации. По оси абсцисс- время в мс, по оси ординат - проводимость мембраны в мС/см2. Цифры около кривых показывают сдвиг МП от ПП по направлению к нулю или еще дальше в сторону положительных потенциалов. Точки показывают значения, полученные в эксперименте, а кривые - результат решения уравнений Ходжкина- Хаксли. |
Открытые биологами механизмы были описаны математически исследователями Ходжкиным и Хаксли. Математические формальные конструкции помогли установить аналогии и принять на вооружение электрические аналоги для быстрого моделирования процессов, происходящих в нервной системе.
Модель 1 (Ходжкина - Хаксли)
Данная модель описывает микродинамику нейрона:
C(dV/dt) = qK(V - VK) + qNa(V - VNa) + I(t);
qK = qKmax + n4;
qNa = qNamax + m3h;
dn/dt = an(1 - n) - bnn;
dm/dt = am(1 - m) - bm;
dh/dt = ah(1 - h) - bhh;
an = 0.7e-V/20;
am = (0.1(V - 25))/(1 - e)(25 - V)/10;
ah = (0.01(V - 10))/(1 - e)(10 - V)/10;
bn = 0.125e-V/80;
bm = 4e-V/18;
bh = 1/((1 - e(30 - V)/10)).
Нейрон проводит электрический сигнал, но не так как металлический проводник, однако он может быть смоделирован на цепях электрических компонент, таких как сопротивления и емкости. Особенностью цепей является: их активный характер (наличие источников напряжения в их составе), разнонаправленностью источников, имитирующих натриевую и калиевую проводимость, нелинейные характеристики сопротивлений.
Части мембраны связываются электрически между собой, составляя пространственные цепи.
Движение возбуждения импульса происходит благодаря тому, что предыдущий фронт возбуждает следующий. Достаточно одиночного импульса в некоторой части цепи, имитирующей нерв, как вдоль цепи начинает распространяться электрический импульс. При этом через некоторое время участок цепи, проведя импульс через себя, приходит в исходное состояние.
|
|
| Рисунок 10.7 - Схемы, поясняющие механизм распространения возбуждения по нервному волокну: а - эквивалентная электрическая схема нервного волокна, участок 1 возбужден, конденсатор С1 перезаряжается, в цепи идет ток от С2 и от С3 к С1 (сила тока показана толщиной стрелок), в следующий момент перезарядится конденсатор С2; б - иллюстрация к теории местных токов Германа; в - распространение нервного импульса связано с изменением проводимости мембраны: передний фронт ПД обусловлен потоком входящих ионов натрия, а задний - выходом из волокна ионов калия. |
Распространение импульса имеет свои особенности.
Рефракторный период (время, в течении которого клетка невосприимчива к возбуждению) - мешает распространению импульса в другом направлении. По аналогии, так выжженная трава противостоит пожару, так как пепел не может воспламениться. Но по мере того, как трава вырастает и восстанавливается, она снова может провести через себя фронт огня.
Одна случайно возбужденная клетка не может возбудить соседние - ее заряд мал, и его глушат заряды соседних клеток. На рисунке показан характер передачи сигнала по нервному волокну на модели Ходжкина-Хаксли.
|
|
| Рисунок 10.8 – Передача электрического импульса по нервному волокну |
Поскольку нервная ткань может иметь двухмерное распределение (например, сердечная мышца), то возбуждение может распространяться по полю нервных клеток – синцитий. При этом рассмотренные ранее свойства позволяют наблюдать ряд особенностей, благодаря которым мы являемся живым организмом.
Фронт возбуждения самопроизвольно выпрямляется.
Если импульс встречает препятствие, то фронт может начать двигаться по спирали (генератор импульсов). Так в сердечной мышце импульс начинает поворачивать вокруг аорты, становясь генератором волн сокращения сердца (рисунок 10.9).
Постоянный ритм работы организма обеспечивается сглаживанием, усреднением, рефрактерностью и самосинхронизацией ансамблей клеток.
|
|
| Рисунок 10.9 – Поле синцитий. Возбуждение и рефрактерный период клеток в сочетании с диаметром дырки в поле позволяют природе создать незатухающий генератор импульсов |
На следующем рисунке показано изменение электрического потенциала в отдельно взятом сечении поля.
|
|
| Рисунок 10.10 - Изменение электрического потенциала синцитий в отдельно взятом сечении их поля |
Сделайте расчет модели Ходжкина-Хаксли для одного из случаев возбуждения.
На ее основе самостоятельно постройте плоскую модель синцитии. Добейтесь синхронной работы двух кольцевых генераторов волн.
Спроектируйте схему руки, которая достает пальцем до носа (не менее 3 сочленений мускулов) и продемонстрируйте ее работу.
Спроектируйте сеть сказки Ш. Перро «Красная шапочка»: вход - параметры личностей персонажей и обстоятельства, выход – действия персонажей, сюжет произведения.
Введите в сеть нечеткие нейроны. Покажите , как меняется сюжет сказки в зависимости от значений параметров персонажей (варианты таблицы истинности и текст сказки, вывод).
| О руководителе курса «Моделирование систем» | Лекция 02. Линейные регрессионные модели | ||||||||||||||||
|
|||||||||||||||||