|
Обучение
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
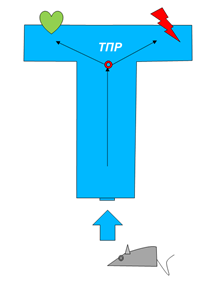
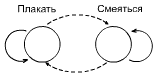
Эксперимент заключался в том, что животное (например, мышь) запускали в Т-образный лабиринт. Пройдя точку принятия решения (ТПР), мышь поворачивала налево или направо. В каждом из концов лабиринта мышь ждало или наказание (удар током), или поощрение (сыр) в зависимости от настроек среды. Естественно животное ничего не знало о расположении поощрений и наказаний.
|
|
| Рисунок – Схема эксперимента по выяснению свойства «обучаемость» у животных |
Существует 3 режима функционирования среды:
- детерминированная,
- стохастическая стационарная (наказания случайны, но их вероятности постоянны во времени),
- стохастическая нестационарная (наказания случайны и их вероятности со временем меняются).
Вариант 1. Допустим, что слева всегда – поощрение, справа – всегда наказание. Сначала мышь поворачивает наугад – налево или направо. Если вправо, то получает наказание. Второй раз, пытаясь избежать наказания, она поворачивает влево. После получения поощрения мышь привыкает поворачивать направо, чем демонстрирует разумность своего поведения в дальнейшем. Вывод: мышь обучилась.
Среда не меняет никогда своих правил. Мышь не знает, куда надо идти. Но в процессе деятельности у мыши появляется понимание (появляется модель, правило), куда следует идти, куда – нет.
Вариант 2. Слева появляется поощрение с вероятностью Рп = 0.7 и наказание с вероятностью Рш = 0.3. (Рп + Рш = 1). Факт появления поощрения или наказания заранее неизвестен никому, случаен. Но в среднем в 7 случаях из 10, когда мышь выбирает левую часть лабиринта, она поощряется, а в 3 случаях - наказывается, что сбивает ее с толку.
Справа назначим поощрение с вероятностью Рп = 0.2, а наказание Рш = 0.8. Поскольку Рп + Рш = 1, то оперировать далее будем только штрафами (поощрения можно легко вычислить по формуле).
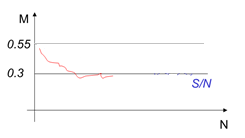
Мышь принимает решение, ее наказывают, она меняет решение, привыкает к поощрениям, однако ее снова наказывают уже за то, что она привыкла считать правильным, и она снова меняет решение, уже построенную модель поведения … Процесс идет сложный, но как показывают эксперименты с животными и человеком, разумные существа в состоянии вычислить, куда им выгоднее в среднем идти, несмотря на то, что среда все время сбивает их с толку. На графике показана кривая обучения со временем для животного, способного обучиться.
|
|
| Рисунок – Характерный график поведения животного, способного к обучению, М – средний штраф, полученный за все время обучения, N – число актов обучения (экспериментов) |
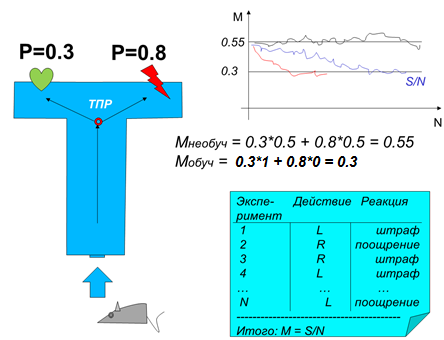
Подсчитаем количество штрафов М, которое приходится на «глупую» мышь, которой все равно, куда поворачивать: 50 на 50.
М = 0.5.*0.3. + 0.5.*0.8. = 0.15 + 0.40 = 0.55.
Подсчитаем количество штрафов М, которое приходится на супер «умную» мышь, которая сразу как-то поняла, куда выгоднее сворачивать:
М = 1*0.3 + 0*0.8 = 0.30.
Очевидно, что избежать штрафов умной супер мыши совсем не удастся, таковы среда и ее правила, но минимизировать их в своей жизни можно.
Показатели всех остальных мышей будут располагаться в промежутке между 0.3 или 0.55 (кроме специальных случаев – мазохизм, удача).
То есть, если лаборанту провести с мышью N экспериментов (например, N = 100) и подсчитать, сколько раз S мышь ударили током в том или другом конце лабиринта (без разницы каком), то легко вычислить экспериментальное значение переменной М, как М = S/N. И сразу выяснить, уровень обучаемости конкретного животного. Для этого достаточно вести лабораторный журнал экспериментов.
|
|
| Рисунок – Схема эксперимента «обучение мыши» |
Если вычислять интервалами по 10 экспериментов (методом скользящего среднего), то можно увидеть динамику обучения: как постепенно мышь переходит от М = 0.55 к М = 0.3.
Таким способом можно замерить второй параметр в модели обучения – скорость обучения. На графике на рисунке отражен характер постепенно обучения мыши, достаточно сравнить синий и красный графики.
В рейтинге обучаемости важно и то, что мышь достигает определенного уровня понимания ситуации, и то, что делает она это быстро или медленно.
Красной линией показан лучший случай – сообразительной мыши, синей – умной, но медлительной мыши, черной - глупой.
Итак, ясность, что должно делать искусственное устройство, чтобы обладать свойством обучаемости, есть.
Автомат Цетлина с линейной тактикой (АЛТ)
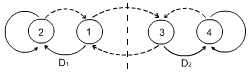
Цетлин построил автомат, который в состоянии обучаться в детерминированной и стохастической стационарной средах – автомат с линейной тактикой. Обозначается: АЛТ [D, Q]. Параметры: D – количество действий, совершаемых автоматом, Q – глубина лепестка автомата.
На рисунке изображен автомат АЛТ[3, 4].
|
|
| Рисунок – Автомат Цетлина с линейной тактикой, АЛТ [3, 4] |
Допустим действия D = {d1 – идти налево, d2 – идти направо, d3 – идти назад}. Если реакцией среды на действие автомата d является поощрение, то автомат переходит в состояние лепестка более глубокое, чем текущее (по сплошной стрелке), иначе – наоборот, всплывает из глубины лепестка или вовсе покидает лепесток, меняя действие на следующее (по штриховой стрелке).
Например, если задать среду как Pш = {0.8, 0.4, 0.7}, то за действие d1 вероятность штрафа составит в среднем 8 случаев из 10, за действие d2 – 4 случая из 10, а за действие d3 – 7 случаев из 10. Ясно, что если автомат начнет с любого состояния (автомат может находиться одномоментно только в одном из состояний), то попав в лепесток 1, он долго там находиться не будет, потому что в среднем на 2 шага вглубь он будет делать 8 шагов из лепестка. И быстро покинет этот лепесток и перейдет к эксперименту над действием d2. Поскольку здесь на 6 шагов вглубь лепестка (поощрение) в среднем приходится 4 шага из лепестка (наказание), то в основном автомат будет находиться внутри лепестка. Однако, рано или поздно (скорее поздно) случится так, что подряд придет 4 штрафа, что заставит автомат сменить лепесток d2 на d3. Долго он там не пробудет, 3 «за» и 7 «против». Автомат снова начнет менять тактику.
Подводя итог, заметим, что автомат улавливает логику среды, подстраиваясь под ее вероятности, которые ему неизвестны. Мы скажем так, автомат строит модель среды и начинает вести себя соответственно этой модели, целесообразно.
|
|
| Рисунок – Доверчивый автомат Кринского |
На рисунке изображена также модификация АЛТ – автомат Кринского, доверчивый автомат. Темперамент автомата слегка меняется (можно моделировать темперамент структурой автомата), но автомат ведет себя также целесообразно в вариантах 1 и 2.
Доверчивым его назвали потому, что часто так себя ведут дети. Если наказывать ребенка за проступок d1, то приходится это делать неоднократно, чтобы «дошло». Однако, если похвалить ребенка, то все обиды забываются мгновенно.
Известны автоматы Роббинса, Крылова (осторожный)... и все они обладают способностью принимать целесообразные решения в стохастической стационарной среде, строя ее модель и решая на ней задачу своего рационального поведения.
Легко сообразить, что рассматриваемые автоматы легко справляются со средой в варианте 1 и 2. Более того, чем больше глубина лепестков автомата, тем меньше штрафов такой автомат получит суммарно за свою жизнь. Консервативное поведение играет здесь автомату на руку. То есть целесообразность автомата растет с ростом величины Q.
В идеале: целесообразность автомата возрастает при «Q -> ∞». А именно: чем больше глубина лепестка автомата, тем (при преобладании поощрений над наказаниями) глубже автомат «зайдет» в лепесток, тем дольше он там будет находиться и тем дольше будет выполнять правильное с точки зрения окружающей среды действие. И наоборот, если наказания преобладают над поощрениями, то действие быстро меняется на другое.
Вариант 3. Стохастическая нестационарная среда. То есть в тот момент, когда автомат понял условия игры и построил модель, среда меняет правила и перестраивает вероятности. То, что было раньше «плохо», становится вдруг «хорошо». Это достаточно обычная ситуация в нашем быстроменяющемся мире. То, что Вам не разрешали в детстве, теперь – можно. То, что разрешали, теперь – непростительно.
Сумеет ли автомат понять, что модель мира изменилась, сумеет ли автомат перестроить свою модель? Да, но вывод о «Q -> ∞» уже не верен.
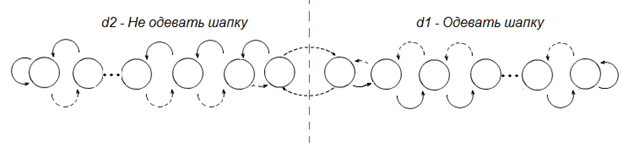
Рассмотрим АЛТ[2, 90] с действиями D = {«одевать шапку», «не одевать шапку»} в условиях средних широт Земли.
|
|
| Рисунок – двухлепестковый «глубоко инерционный» консервативный автомат Цетлина АЛТ [2,90] |
Пока на дворе властвует зима, автомат надевает шапку и каждый день поощряется средой, загоняя себя вглубь лепестка на 90 позицию (у нас зима 180 дней в году). Однако, когда наступает лето, он продолжает упрямо надевать шапку до середины лета, получая, конечно, штраф от среды и возвращаясь к основе лепестка d1 и, в конце концов, меняя действие d1 на d2. За 90 оставшихся дней автомат научается «не надевать шапку». И тут снова среда меняет свои правила – и половину зимы автомат ходит без шапки.
Признать такой автомат целесообразным здесь уже нельзя.
Попробуем наоборот - уменьшить инерционность (консервативность) автомата Q. Рассмотрим АЛТ [2, 1].
|
|
| Рисунок – Атомарный автомат «Иван-дурак», АЛТ [2, 1], Q->0 |
Автомат с авантюрным поведением (Q->0), как мы это раньше обсуждали, тоже часто не подходит для решения задач, оказывая плохие результаты по показателю М. Накопить сведения, обобщить опыт он не в состоянии и часто попадает впросак.
Становится ясно, что необходим автомат с таким Q, который наилучшим образом подходит к каждой новой задаче, настраивает Q на нее, оптимизирует величину Q.
Такой автомат был сделан – автомат с переменной структурой, АПС.
Автомат с переменной структурой, АПС
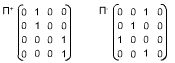
Как известно, схему автомата (граф) можно представить матрицей, перенумеровав все его состояния. Если из состояния i в состояние j есть переход, то в ячейку матрицы (i, j) ставится 1, иначе - 0.
Так, автомат
|
можно представить матрицами П+ и П-:
|
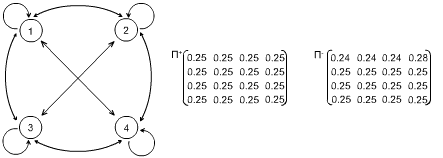
Теперь представим, что автомат - не обучен и ему все равно, какой переход делать (вероятности перехода из состояния 1 в состояния 1, или 2, или 3, или 4 равны, то есть 0.25), как это показано на рисунке.
|
С помощью генератора случайных чисел мы всегда можем сделать выбор для перехода из одного состояния в другое. Однако, если выбор хоть и сделан, но не верно (последовало наказание), автомат сам меняет вероятности в матрице.
Конкретно, автомат уменьшает вероятность в ячейке, которая указала на неверный выбор, перераспределяя в равной степени доли ее значения в соседние по строке ячейки так, чтобы сумма вероятностей перехода (сумма по строке) оставалась равной 1 (полная группа несовместных событий).
Так постепенно шаг за шагом в матрице (в выгодных ее местах) начнут появляться в отдельных ячейках числа, близкие к 1, а в других (невыгодных) – близкие к 0. Фактически автомат задаст собственную структуру для конкретных правил конкретной среды, построит сам себя, построит модель. При этом глубина Q автомата будет оптимальной.
Матрицу в общем смысле можно ассоциировать со связями в нейронной сети. Поощрение – это возбуждающая связь нейронной сети, наказание – тормозная.
При перестройке среды автомат начнет снова видоизменяться, отслеживая реакции среды на свои действия.
Вывод: в стохастической нестационарной среде автомат с переменной структурой может вести себя целесообразно.
Общий вывод: можно построить такую искусственную систему, которая будет себя вести целесообразно (обучаться, строить модель среды, адаптироваться к окружающему миру, познавать его) в каждом из трех вариантов сред.
Эпилог «Кем нам быть: авантюристами или консерваторами»
Цетлин снял характеристики, какого уровня целесообразности может достичь автомат в случае изменчивости δ нестационарной среды и какова при этом будет его оптимальная глубина лепестков q. График приведен на рисунке.
|
|
| Рисунок – График зависимости средних штрафов М автомата Цетлина от его инерционности q (коэффициента темперамента А:К) и показателя изменчивости среды δ: М(q,δ) |
Если среда меняет значения своих вероятностей 1 раз за 1000 эпох, то ее изменчивость δ равна 0,001. При таких редких изменениях среды следует придерживаться значений q = 5-6. Увеличение q (консерватизма) приведет к излишним штрафам за счет инерционности, не восприятию новаций. Уменьшение q (увеличение авантюризма) приведет тоже к увеличению штрафов (причем даже более резкого, чем за консерватизм) за счет беспорядочных метаний, хаотического поведения индивидуума. Соотношение удач к неудачам в оптимальном варианте qопт составит 2 к 1. Неплохо!
Если среда чаще меняет значения своих вероятностей, например, 1 раз за 10 эпох, то ее изменчивость δ равна 0,1. В этом случае штрафы растут и у авантюриста, и у консерватора («во время войны плохо всем»). В такой среде жить сложнее – правила все время меняются. Но значение q смещается в сторону 3-4, то есть авантюризма, поскольку на войне легче выжить, моментально реагируя на новые обстоятельства. Кривая M(q) становится все более симметричной, острой, а штрафы растут. На войне как на войне.
Вывод: Консерватором правильнее быть в более спокойное время. Ошибаться лучше в сторону увеличения q («если не знаешь, как поступить, затаись»). Женское поведение более консервативно, более мирно. Мужское – более авантюристично, более агрессивно. Когда мир меняется, надо соответствовать его изменениям и меняться самому, но …
«Не дай Вам Бог жить в эпоху перемен».
Китайская мудрость.
Критерием выживания разумного организма является минимизация рисков. Минимизация рисков имеет две составляющих – сохранение и развитие. Ни то, ни другое не есть абсолют. В зависимости от условий окружающей среды в ряде случаев выгоднее консервативное поведение (традиционное «сохранение»), в других – авантюрное («развитие»). И то, и другое поведение – необходимость. Важно уметь переходить при необходимости от одного к другому – от обороны к нападению, и наоборот.
К консервативному поведению более тяготеют женщины, чья физиология и психология эволюционно направлена на поддержание и сохранение семьи, детей, дома. Они более осторожны (трусливы), склонны к накоплению ресурсов, сидению дома, защите. К авантюрному – мужчины, направленные на добычу, разведку, защиту, агрессию, новизну, модернизацию, развитие.
В каждом человеке есть в определенной пропорции составляющая «развития» и составляющая «сохранения». В тяжелые моменты сдвиг происходит в сторону сохранения любой ценой жизни и достигнутого. В благоприятные моменты сдвиг происходит в сторону развития, поскольку сохранение обеспечено и хочется чего-то большего.
Следует понимать, что мужское поведение более расточительно, неудач здесь больше по отношению к доле неудач при поддержании тактики консерватора. Оптимальным является правильное сочетание А и К стратегий (коэффициент темперамента = А:К) в соответствии с параметром изменчивости среды δ.
Интересно, что на основе описанных экспериментов был составлен рейтинг животных по степени сообразительности, способности обучаться. Вполне ожидаемо места в первой десятке заняли дельфины, свиньи, во’роны, … . Человек занял в этом рейтинге 4-5 место. После разбора этого удивительного факта удалось выяснить, что если разделить людей на классы мужчин и женщин, то женщины занимали первые места, а мужчины - восьмые-девятые (в среднем 4-5 место), портя статистику.
Эксперимент ставился на стенде.
|
На экране человеку поочередно демонстрировались разнообразные картинки, похожие на те, что нарисованы на дверях шкафчиков в детском саду.
|
Компьютер случайным образом «задумывал» закономерность - например, «красные И съедобные». Перед человеком стоял выбор (две кнопки): принять очередную картинку (Да) или отвергнуть (Нет) – соответствует картинка задуманной закономерности или нет. Если выбор был неверный (нажата не та кнопка), то раздавался неприятный сигнал или следовал удар человека током. Если выбор кнопки соответствовал задуманной закономерности, то неприятности отсутствовали (приятная мелодия, похвала).
Надо сказать, что и мужчины, и женщины довольно быстро улавливали скрытую от них изначально закономерность, ориентируясь только на поощрения и наказания среды. И все чаще в процессе эксперимента правильно делали свой выбор – нажимали нужную кнопку. Общая статистика M(N)=S/N постепенно улучшалась, сигнализируя экспериментаторам о способности к разумному поведению, обучаемости. Женщины закрепляли полученное, не ошибаясь далее. Однако мужчины время от времени, уловив закономерность, все равно ошибались.
На вопрос мужчине: «Почему, обучившись, поняв закономерность, Вы, тем не менее, поступали нелогично, был получен ответ: «А интересно, что будет?». В отличии от консервативной тактики обучения «сохранения», присущей женщинам, у мужчин была явно выражена компонента «развития», авантюризма. «Вдруг там еще лучше». Поговорка «От добра добра не ищут» для мужчин не работала.
Иногда это оправдывало себя, чаще – нет. Известно, что мужчины чаще погибают, раньше умирают, чем женщины, проявляя склонность к исследованиям, часто опасным, испытывая тягу к новому, неизведанному. Однако, ценой их смерти общество получало новую информацию, полезную для выживания популяции в целом. Мужчины дарят обществу новую информацию, защищая его от гибели.
Вопрос: «Почему? За что?» - Ответ: «За любовь».
Примечание. Так ли страшно, что мужчины погибают чаще женщины, ведь их природная миссия для эволюции популяции человека может оказаться не выполненной? Ответ: Нет, не страшно, если передача генов будущим поколениям от мужчин уже состоялась. Задачу опеки подрастающего поколения женщина выполняет дольше, чем мужчина, и ее возраст дожития, соответственно, выше мужского.
Параметр темперамента в целом предопределяет профессиональные склонности: повара в столовых, воспитатели в детских садах – женщины; а повара в ресторанах, преподаватели в ВУЗах – мужчины.
Кстати, подобные устройства в виде браслетов иногда используют для обучения брокеров, в результате вырабатывая у них так необходимую им интуицию (разумеется в весьма ограниченных пределах).
|
Как выяснилось, автоматы не просто играют в игры, а играют в коллективные игры, дополняя этим друг друга, поддерживая рациональность поведения популяции в целом.
Коллектив автоматов
Если понятно, что автоматы могут вести себя целесообразно, то стоит рассмотреть, как поведет себя коллектив взаимодействующих между собой автоматов.
Сразу отметим, что эксперименты с автоматами показали, что самое устойчивое общество состоит из 40% бесстрастных, 40% умеренных пессимистов и 20% умеренных оптимистов. В этом распределении наблюдается явно выраженная асимметрия. Очевидно, что вымирают сразу оголтелые оптимисты и пессимисты. Оптимисты тоже умирают чаще пессимистов. Пропорцию стоит запомнить.
Покажем, как можно учесть темперамент в принятии решений автоматом. Допустим, что автомат решает: жениться ему (Y = 1) или нет (Y = 0). Решение зависит от двух факторов: невеста умеет готовить (Х1 = 1) и имеет жилплощадь (Х2 = 1). При этом Х1 = 0, если невеста точно не умеет готовить, и Х1 = 0.5, если она говорит, что умеет, однако, реально жених ее стряпню не пробовал. Тоже и с жилплощадью: Х2 = 0 (нет жилья) и Х2 = 0.5 (говорит, что есть).
Y = f(X1, X2). В зависимости от реализуемой логической функции f автоматы могут быть разными по темпераменту: от оголтелых оптимистов, готовых жениться только от намека на положительные качества невесты (0.5), до глубоких недоверчивых пессимистов, женящихся только в случае, если они точно удостоверятся (1), что невеста имеет соответствующие качества (иначе жениться только обещают: Y = 0.5). Набор возможных функций от супер мягких до сверхжестких представлен в таблице.
Таблица – Спектр функций принятия решений
| Умеет готовить | Есть жилплощадь | Варианты поведения при выборе решения Y = F(X1, X2) | ||||
| X1 | X2 | F1 | F2 | F3 | ... | F4 |
| 0 | 0 | 0 | 0 | 0 | ... | 0 |
| 0 | 0.5 | 0 | 0 | 0 | ... | 1 |
| 0 | 1 | 0 | 0 | 0 | ... | 1 |
| 0.5 | 0 | 0 | 0 | 0 | ... | 1 |
| 0.5 | 0.5 | 0 | 0 | 0.5 | ... | 1 |
| 0.5 | 1 | 0 | 0.5 | 0.5 | ... | 1 |
| 1 | 0 | 0 | 0 | 0 | ... | 1 |
| 1 | 0.5 | 0 | 0.5 | 0.5 | ... | 1 |
| 1 | 1 | 1 | 1 | 1 | ... | 1 |
| Оголтелый пессимист | … … … | min(x1,x2) | ... | Оголтелый оптимист | ||
Игры автоматов
Рассмотрим поле – территорию, разделенную на области Каждый участок территории дает населению, живущему на ней, определенный доход, ресурс.
На разных территориях – разные природные условия, разный доход. Доход обозначен числом.
| 100 | 40 | 40 | 40 | 40 | 40 | ... | |
| 40 | 40 | 40 | 40 | 40 | 40 | ... |
Рассмотрим население – 10 автоматов, каждый из них ведет себя целесообразно.
Население распределим по территории случайным образом. Автомат обозначим красным крестиком в клетке.
| 100xx | 40 | 40x | 40 | 40 | 40 | ... | |
| 40xx | 40xxx | 40 | 40xx | 40 | 40 | ... |
Очевидно, что двум автоматам тесно в клетке с доходом 100. Каждый получает по 50. Но они не изменят свое поведение, так как уйти в соседнюю клетку – это означает проиграть. В клетке справа – 40, в клетке снизу - 40/3, в клетке по диагонали – 40/4. Все гораздо хуже! Уйдя в соседнюю клетку, автомат, так как он способен к целесообразному поведению, будет «наказан» и сменит тактику, вернется в клетку 100 (иногда не сразу, но рано или поздно).
А вот автоматы в клетках 40 рано или поздно уйдут в соседние клетки, так как в свободной клетке по 40 гораздо выгоднее существовать, чем в занятой уже кем-то клетке 40, где приходиться делить с кем-то ресурсы.
Если подождать некоторое время, то в пределе автоматы распределятся примерно так:
| 100xx | 40x | 40x | 40x | 40 | 40 | ... | |
| 40x | 40x | 40x | 40x | 40x | 40 | ... |
Это будет устойчивое состояние!!! Оно будет существовать как угодно долго (разумеется с небольшими флуктуациями, но которые все равно будут возвращаться, скатываться, к устойчивому состоянию).
Так как автомату из клетки 100 не выгодно уходить с 50 на 40. В занятую клетку 40 никто не придет вторым, так как есть много пустых клеток по 40, а делить 40 на двоих или троих невыгодно.
В клетку 100 то же никто не придет третьим, так как в этом случае с 40 надо будет перейти с дохода 100/2=50 на доход 100/3=33, что не выгодно.
Такая устойчивая игра называется игрой Нэша.
Валовый продукт, который получит страна в этом случае, составит: 50*2 + 40*8 = 420.
Цена игры Нэша (средняя заработная плата населения) = 420/10 = 42.
Существуют и другие игры.
Например, игра Мора.
| 100x | 40x | 40x | 40x | 40x | 40 | ... | |
| 40x | 40x | 40x | 40x | 40x | 40 | ... |
Так как один автомат будет получать 100, а другие по 40, то рано или поздно какой-то автомат перейдет (пусть случайно) в клетку с 100. Это даст ему выигрыш на 10 больше, чем в клетке 40, так как после перехода он получит 50, разделив 100 на двоих. Бывшему там ранее автомату, конечно, не выгоден такой переход (со 100 его доход меняется на 50), и он может уйти в другие клетки (восприняв понижение дохода как наказание), но все равно вернется в эту клетку 100, так как 50 лучше, чем 40 или даже 33 или менее того.
Однако подсчитаем все-таки цену игры Мора, допустив, что как-то распределение, показанное на рисунке, сохранится, хотя оно и неустойчивое.
Валовый доход, который получит страна в этом случае, составит: 1*100 + 9*40 = 460.
Цена игры Мора (средняя заработная плата) = 460/10 = 46.
Вывод: цена игры Мора (46) выше цены игры Нэша (42). В игру Мора играть выгоднее, но она неустойчива.
Интересно заметить, что валовый доход страны вырос, и средняя заработная плата по стране тоже выросла, хотя игра неустойчива.
Возникает вопрос: можно ли все-таки сыграть в игру Мора, сделав ее устойчивой?
Да! Такая игра называется игра Мора с общей кассой.
Необходимо каждому автомату ежемесячно, получив доход со своего участка, высылать весь его в центр. Центр, собрав всю сумму по стране, делит ее на все население поровну. И высылает эту сумму в регион: по 46 каждому.
Теперь условие устойчивости сохранено. Каждый получает по 46 и лезть к соседу не имеет смысла.
Более того, если автомат по случайности залезет в соседнюю клетку, то доход там разделится на двоих. Общий валовый доход страны упадет: 1*100 + 2*20 + 7*40 = 420 и после трансфертов каждый житель страны получит не 46, как ранее, а по 42. Таким образом автомат (и остальные автоматы тоже!) получит наказание в виде уменьшения суммы на 10% и начнет возвращать утраченное состояние. Вполне возможно, что другие автоматы тоже, почувствовав наказание, начнут менять свое состояние. Население в любом случае задвигается и восстановит прежнее устойчивое распределение: 1*100 + 9*40 = 460 и прежнюю цену игры - 46.
Вывод: можно сделать выгодную игру Мора устойчивой, если усовершенствовать ее механизмом общей кассы.
Легко видеть, что игра Нэша имитирует личные интересы, а игра Мора – общественные.
Нетрудно догадаться, что речь идет о налогах.
Обратите внимание!!! Кто-то, зарабатывая 100, получает 46. А некто, зарабатывая 40, получает 46. На лицо – неравенство, но … неравенство в оплате эквивалентно выгоде общего интереса, так как общество в целом выигрывает, цена игры Мора выше цены игры Нэша. Налоги в стране являются стабилизатором общественного устройства. Налоги повышают общий эффект в стране (в консервативном варианте поведения).
Платя налоги, и общество выигрывает, и каждый (почти) его член. Кроме того, страна остается стабильной.
Стабильность игры тем выше, чем меньше автоматы дергаются. Если они, найдя лучшее состояние, не стремятся его менять (консервативны, обладаю большим значением q), то страна и ее жители постоянно выигрывают. Если среди автоматов находится авантюрист, который все время дергается и заставляет дергаться снова и снова других в поисках нового выгодного состояния, страна во время поисков теряет.
Однако, если ситуация в стране меняется, меняются цены регионов, то авантюрные поиски полезны, они переводят страну в новое лучшее состояние.
Конечно, налог платит больше тот, кто больше получает. Автомат в клетке 100 уплачивает 54 единицы налога, так как «туда» посылает 100, а «оттуда» получает 46. Остальные дотируются по 6 единиц. Условно говоря, проигравший один, а выигравших - много. Естественно, такой автомат часто предпринимает меры по сокрытию своих налогов, переводу их в закрытые зоны, фонды, формы.
Поэтому общество должно строго следить за выполнением правил игры, обеспечивая свою стабильность и эффективность игры Мора. Нарушение правил для страны – смерти подобно. Тем более, что находится автомат на богатой территории или на бедной – есть игра случая. В качестве компенсации в конце концов для удовлетворения амбиций обиженного следует давать ему небольшой добавочный процент по отношению к средней зарплате.
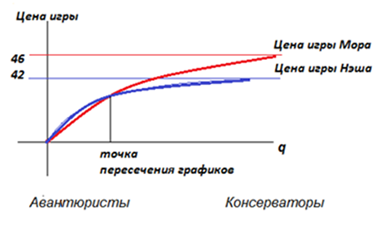
Все, конечно, сильно зависит от глубины q автомата. Цетлин снял характеристику, показывающую цену игры от величины q, которая связывается с темпераментом (шкала «авантюризм – консерватизм»).
|
|
| Рисунок – График зависимости цены игры М от глубины автомата q |
Чем более целесообразен автомат, тем более выгодно ему играть в игру Мора с общей кассой (социализм). Чем более консервативен автомат, тем более выгодна ему игра Мора.
М.Л. Цетлин называл этот эффект - «выигрыш социалистического общества при высоком уровне сознательности его членов». Совместное принятие решений, уважение и координация реализуют более выгодные стратегии для общества в целом, позволяя оптимально распределять производительные силы общества в борьбе с природой.
В этом выигрыше (в нашем примере 46 - 42 = 4, то есть 10% ВВП), кстати, находятся излишки, которые мы можем себе представить, как запасы общества для гашения последствий экстремальных ситуаций.
Но если эгоистичные действия элит преобладают над общественными интересами, то страна деградирует, сползает с наилучшей точки цены Мора. Общество «падает», часто не понимая, что происходит, и кто виноват.
Интересно отметить, что при консервативном поведении общества в целом, выигрыш в системе Мора выше – красная линия на графике выше синей линии. Однако есть точка пересечения графиков, после которой с понижением глубины автоматов выгоднее играть в игру Нэша. В любом случае социализм – это сознательность. Если сознательность низкая – то цена игры Мора снижается и может оказаться даже ниже игры Нэша. При низкой сознательности выгоднее играть в игру Нэша. Но при высокой сознательности (консерватизме) цена игры Мора выше цены игры Нэша.
Сознательность сдерживает автоматы от авантюристических поступков. Хотя есть и другие механизмы закрепления населения в своих ячейках (прописка, концлагерь, цифровые деньги, искусственное изъятие дохода у общественной массы и так далее).
Капитализм, индивидуализм – это ярко, играет на личных интересах, но проигрывает в тот момент, когда требуется напряжение всех сил общества в борьбе с глобальной опасностью. Авантюрист легче ищет новые ниши, однако, чаще погибает. («Седых брокеров не бывает» Насим Талеб).
Как ранее было отмечено, при частом изменении правил среды выгоднее авантюрное поведение, так как оно позволяет уловить новые ранее неизвестные возможности.
Требуется отметить, что в модели существуют эффекты второго порядка.
Например, при игре Мора с общей кассой (социализм) один из автоматов может вовсе перестать вносить в кассу какой-либо доход (не работать), но получать доход (незаслуженную зарплату) из центра.
Общество, потеряв один из источников дохода, проигрывает: 1*100 + 8*40 + 1*0 = 420. Цена игры: 420/10 = 42 вместо 46.
В этом случае ситуация лично выгодна самому автомату, так как, затрачивая 0, он получает 42. Конечно, раньше он получал 46, сейчас - 42. Но рентабельность (Результат/Затраты = 42/0 >> 46/40) при такой игре бесконечна, как бесконечно значение частного после деления делимого на ноль (42/0=∞).
Общество после потери своего члена слегка деградирует – точка сползает по красному графику влево вниз, приближаясь к синему уровню цены Нэша. После этого еще один член социалистического общества замечает, что не работать выгодно. Личные интересы начинают преобладать над общественными. Общество разваливается, если не принимает мер против саботажников. Обычно за счет информационного взаимодействия и отрицательного примера такая лавина нарастает. И рабочая точка начинает с ускорением двигаться влево вниз (работает положительная обратная связь). Ситуация становится неустойчивой, если элиты ее не остановят.
(Чаще всего именно они, обиженные клеткой 100 и трансфертом 56, подталкивают общество к разрушению, не понимая последствий лично для них. В элитной среде считается, что на их век хватит. Однако, элиты всегда недоучитывают эффект лавины, которую уже нельзя остановить).
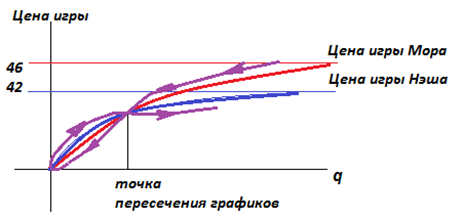
Общество может даже проскочить точку пересечения кривых Нэша и Мора на графике, дойдя до нуля!
После этого возникает перестройка общества на новый тип сознания (авантюристический) и новый тип игры (Нэша). И общество начинает двигаться вправо вверх по синей линии, так как эта тактика более выгодна при низких уровнях q (синий график выше красного), а игра устойчива. Общество делает в своем развитии петлю.
|
|
| Рисунок – Общество деградирует и описывает петлю: переходит от игры Мора к игре Нэша (при q->0), затем начинает «выздоравливать», двигаясь по Нэшу (q->max) |
Лавину, не доводя до петли, можно остановить в районе точки пересечения, если вводить в общество элементы пропаганды, воспитания или народного капитализма (как это, к примеру, делалось в Китае, во Вьетнаме, в Югославии). Однако лучше ситуацию вовсе не допускать до сползания, вовремя останавливая процесс саботажа общественных интересов со стороны отдельных членов общества, волей судеб получающих высокие вознаграждения (авторские за публичные произведения, доступ к управлению финансовыми потоками, передача нажитого по наследству, земельная рента и рента на полезные ископаемые, доступ к сетевым информационным ресурсам).
Пример
В практике предприятий используется производственная функция, которая показывает доход предприятия в зависимости от существенных переменных.
Примем два лесозаготовительных участка (2 клетки страны) с населением 100 рабочих. Рабочих можно распределять по участкам: на первый – Х рабочих, на второй – У рабочих.
То есть, уравнение: Х + У = 100.
Зарплата на первом участке формируется как S = 400*Х - 0,02*Х3.
Смысл уравнения: на первом участке растут толстые деревья, которые находятся на нормальном расстоянии друг от друга, лес не требует предварительной расчистки, каждый рабочий, свалив дерево, хорошо зарабатывает, зарплата 400. Однако, рабочие мешают друг другу (надо соблюдать правила техники безопасности), поэтому надо отходить друг от друга подальше в поисках нового дерева – отрицательное слагаемое, символизирующее затраты, Х3 с небольшим коэффициентом 0.02. Переход «подальше» требует усилий – снег, перенос бензопилы – поэтому функция при увеличении Х быстро нарастает (в кубе).
Зарплата на втором участке формируется как Р = 280*У - 0,4*У2.
Смысл уравнения: на втором участке растут более тонкие деревья, которые находятся на небольших расстояниях друг от друга, лес требует предварительной расчистки, каждый рабочий, свалив дерево, зарабатывает только 280. Рабочие тоже мешают друг другу, но удар от тонкого дерева менее болезненный. Появляется медленное слагаемое У2, но с большим коэффициентом 0.4.
Итак, имеем:
Х + У = 100
S = 400*Х - 0,02*Х3
Р = 280*У - 0,4*У2
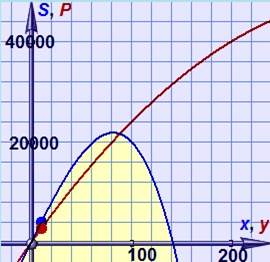
Построим функции S(X) и P(Y), чтобы понять их «физический» смысл.
|
|
| Рисунок – Графики производственных функций |
Распределить рабочих по участкам {X, Y} можно по-разному.
- 1. S = P. Крайний Север и Дальний Восток должны быть развиты одинаково, как и Центр России. Везде живут наши люди и имеют одинаковое право на горячую воду, газ, театры, фрукты.
- 2. S/X = P/Y. Важно, чтобы зарплаты везде были одинаковы. Люди не виноваты, что в Твери нет нефти… Страна у нас единая, все равны. Бросать Дальний Восток тоже плохо, не в Москве же всем жить.
- 3. S + P -> max. Главное, каждому работать изо всех сил на своем месте, каждый даст стране все, что может. А потом разделим все суммарное богатство на всех поровну.
- 4. X = У. Главное, не наступать друг другу на ноги, равномерно расселиться по всей стране, осваивая максимально все ее богатства.
- 5. X*S > Y*P. Большинство людей живет лучше меньшинства. Диктатура большинства. Вариант 1: X(S/X > P/Y) > Y – людей Х, получающих больше зарплату, чем у людей Y, больше. Вариант 2: денежная масса первого класса больше денежной массы второго класса (они скинутся и задавят). Вариант 3: людей в богатой стране больше, чем людей в бедной стране Х(S > P) > Y.
Как видите, это разные стратегии развития страны. Все хорошие. Решите 5 раз задачу с тремя уравнениями, дополнив их каждый раз одним из уравнений (стратегией).
Примечание: как видите, мы строим с Вами модели и ищем среди них наилучшие, пока, правда, вручную.
Найдите значения (Х, У) в каждом случае.
Заполните таблицу 1. Найдите зарплату на каждом участке, общий доход страны, среднюю зарплату по стране, сколько надо заплатить от одного участка другому, чтобы рабочие не бегали в одного участка на другой за более высокой зарплатой.
Х – население первого участка, чел.
S - фонд з/п на первом участке, руб.
S/X – средняя зарплата на первом участке, руб.
Y – население на втором участке, чел.
P - фонд з/п на втором участке, руб.
P/Y – средняя зарплата на втором участке, руб.
N = |S - P| - неравенство развития регионов
Z = |S/X - P/Y| – неравенство зарплат в регионах
S + P – доход страны
(S + P)/(X + Y) – средняя зарплата по стране
Таблица 1 – Варианты применения стратегий на предприятии
| Вариант | Х | У | S | P | N | S/X | Р/Х | K | S+P | (S+P)/(X+Y) |
| Равенство развития территорий | ||||||||||
| Равенство зарплат на территориях | ||||||||||
| Максимальная сумма произведенных товаров в стране | ||||||||||
| Равномерное распределение населения по территории страны | ||||||||||
| Большинство людей живет лучше меньшинства |
В каждой строке таблицы сделайте вывод: отметьте достоинства и недостатки стратегии.
Обратите внимание на то, что невозможно совместить несколько решений в одну стратегию. Решения разные и придется выбирать.
Обратите внимание: решение поменяется, если изменить числовые параметры функций. А если поменять вид функций – вообще может поменяться все, не только количественно, но и качественно. В странах с различной территорией, различным населением, различными природными условиями производственные функции различны. Значит, в различных странах решения могут кардинально отличаться друг от друга.
Подумайте, как могут выглядеть производственные функции для коллективной охоты на крупного зверя или сбора артелью диких грибов в лесу.
Ответ надо спрятать в ссылку с паролем
Ответ:
| Вариант | Х | У | S | P | N | S/X | Р/Х | K | S+P | (S+P)/(X+Y) |
| Равенство развития территорий | 41 | 59 | 15022 | 15128 | 106 | 366 | 256 | 110 | 30149 | 301 |
| Равенство зарплат на территориях | 80 | 20 | 21760 | 5440 | 16320 | 272 | 272 | 0 | 27200 | 272 |
| Максимальная сумма произведенных товаров в стране | 51 | 49 | 17747 | 12760 | 4987 | 348 | 260 | 88 | 30507 | 305 |
| Равномерное распределение населения по территории страны | 50 | 50 | 17500 | 1300 | 4500 | 350 | 260 | 90 | 30500 | 305 |
| Большинство людей живет лучше меньшинства | 70 | 30 | 21140 | 8040 | 13100 | 302 | 268 | 34 | 29180 | 291.8 |
| О руководителе курса «Моделирование систем» | Лекция 02. Линейные регрессионные модели | ||||||||||||||||
|
|||||||||||||||||