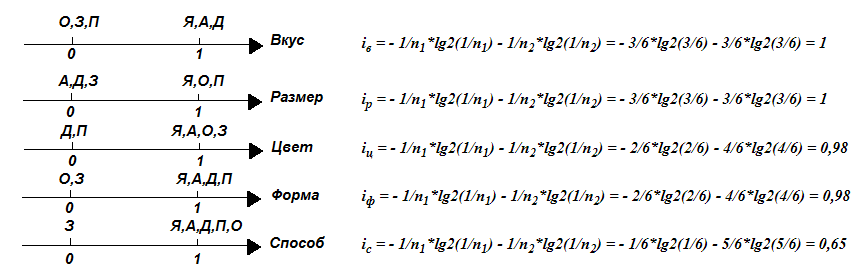|
Практическое занятие 4
|
|
|
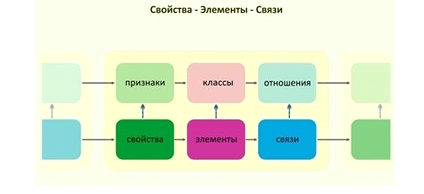
| Рисунок – Основные категории мышления |
|
|
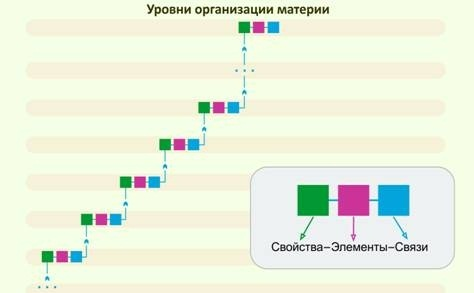
| Рисунок – Уровни организации материи. Свойства порождают элементы, элементы порождают связи. Элементы и связи – это системы, которые проявляют новые свойства на новом уровне организации материи |
Предмет, вещь, сущность — одна из основных категорий нашего сознания, отдельный объект материального мира, обладающий относительной независимостью, объективностью и устойчивостью существования.
Предмет характеризует количественную характеристику материи и задается своими структурными, функциональными, качественными и количественными характеристиками. Наиболее общим выражением собственных характеристик сущности являются её свойства, а место и роль данной вещи в определённой системе выражаются через её отношения с другими вещами.
Предмет в речи обозначается именем существительным, которое является пересечением свойств, выражаемых именами прилагательными.
Формально записывается так: P = (X1 = (255, 0, 0)) И (X2 > 100 И (X3 = "сочный")
или так:
P = (X1 = (255, 0, 0))*(X2 > 100)*(X3 = "сочный").
То есть данный предмет Р обладает одновременно (пересечение, знак И, умножение) тремя признаками-свойствами: он красный, он весит больше 100 грамм и он сочный.
Например, перечисление свойств (прилагательных): зеленое И сочное И шарообразное И сладкое сужает воображаемое нами количество объектов и приводит нас к понятию «яблоко». Яблоко – это пересечение этих свойств. Если область определения слишком велика (сюда не входит забор, но входит киви, арбуз), то надо продолжить перечисление свойств, сужая область в пределе до единственного предмета.
|
|
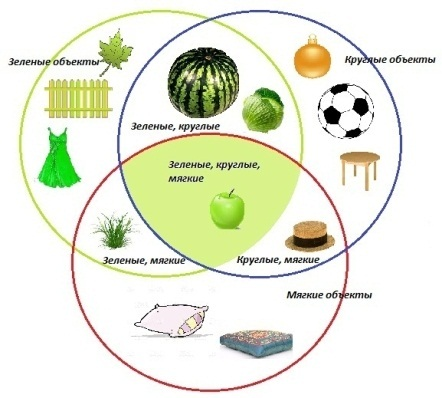
| Рисунок – Диаграмма Эйлера-Венна, показывающая появление содержания предмета из его свойств (в зеленом круге множество зеленых предметов, в красном – мягких, в синем - круглых). В пересечении кругов находятся предметы, обладающие одновременно несколькими соответствующими свойствами |
Объем понятия обратно пропорционален содержанию понятия (его сути).
Объем = 1 / Содержание.
Например, разные яблоки (красные желтые, зеленые, большие, малые, кислые, сладкие, ватные) – объем понятия большой, однако содержание – мало, не конкретно.
Чем точнее описываем яблоко, тем меньше таких именно яблок мы найдем – объем понятия маленький, а содержание большое, четкая формула данного яблока.
Понятие – есть ПЕРЕСЕЧЕНИЕ свойств (И).
Признак – есть объединение свойств (ИЛИ). Например, или красный, или желтый, или синий – все это одним словом «цвет».
Понятие – отображенное в мышлении единство существенных свойств, связей, отношений предметов и явлений, выделяющее и обобщающее предметы до класса по выделенным свойствам с помощью операций сравнения, анализа, синтеза, агрегации, идеализации, обобщения.
Содержание понятия – совокупность существенных свойств и связей предметов, отраженных в понятии. Содержание понятия отражается в смысле слова. Смысл слова – выражает информацию о предмете. Например, содержанием понятия «коррупция» является совокупность двух существенных признаков: «сращивание государственных структур со структурой преступного мира» и «подкуп и продажность общественных и политических деятелей, государственных чиновников и должностных лиц».
О содержании понятия нельзя говорить в отрыве от его объёма.
Объем понятия – совокупность (множество) предметов, объединенных понятием. Объем понятия выражается в значении слова. Например, в понятие яблоко входит и красные, и зеленые, и мелкие, и крупные, и сладкие, и кислые яблоки.
Значение слова – обозначаемый им предмет или класс, или свойство. Например, под объёмом понятия «товар» подразумевается множество всех изделий, предлагаемых рынку для обмена сейчас, в прошлом или в будущем.
Еще пример, «кентавр» – смысл есть, значения нет.
Содержанием понятия «равнобедренный прямоугольный треугольник» будет указание на наличие в составе геометрической фигуры из трех взаимно пересекающихся прямых двух углов, равных 45°. Объемом же такого понятия станет вся совокупность возможных равнобедренных треугольников.
Значение слова – состав класса объектов (элементов), скрывающихся за этим классом, количественная характеристика (насколько легкий, насколько теплый и т.д.). Значение слова обусловлено местоположением его в пространстве системы координат признаков-свойств, плотностью и размерами кластера.
Смысл слова – структура элементов, пересечение образующих их свойств, свойства в своем единстве, то есть связи, качественная характеристика. Смысл двух слов, отличающихся друг от друга состоит в том, что они (центры тяжести их кластеров) находятся в пространстве признаков (осей координат) на определенном расстоянии, в определенном месте системы координат-признаков
Предметы, взятые в объеме, – класс.
Объём понятия может входить в объём другого понятия и составлять при этом лишь его часть. Например, объём понятия «фирменный знак» целиком входит в объём другого, более широкого понятия «знак». При этом содержание первого понятия оказывается шире, потому что содержит больше отличительных признаков, чем содержание второго.
Действует следующий закон: чем шире объём понятия, тем проще его содержание, и наоборот.
Род. Родовым будет такое понятие, объём которого шире и полностью включает в себя объём другого понятия.
Вид. Видовым будет такое понятие, объём которого составляет лишь часть объёма родового понятия.
Вид внутри рода.
Любое понятие может быть полно охарактеризовано при помощи определения его содержания (иными словами – смысла) и установления предметов, с которыми данное понятие имеет определенные связи.
У человека два типа мышления: конкретное и абстрактное.
Основные формы конкретного мышления: ощущение, восприятие, представление.
1) ощущение - выделение единственного, наиболее важного в данный момент свойства предмета материальной деятельности. Ощущения делят на виды по видам чувствительности: осязательные, обонятельные, вкусовые, слуховые и зрительные. Ощущение - настолько простая мысль, что кажется, будто это не мысль, а чувство. Ощущение в ИИ соответствует признакам и свойствам.
2) восприятие - образ, состоящий из двух и более ощущений, это все еще ощущение, только сложное, части которого составляют целостный образ. Восприятие в ИИ соответствует системе признаков-свойств и обозначается элементами-классами.
3) представление - устойчивое восприятие, создаваемое за счет активного подключения памяти. Представление в ИИ соответствует нейронной сети (или какой-либо другой алгебраической форме знаний-уравнений-неравенств).
Основные формы абстрактного мышления: понятие, утверждение, суждение, умозаключение.
Умозаключения строятся из суждений, суждения состоят из утверждений. Утверждения конструируются из понятий с использованием связей (операций, функций, чисел).
Приведем пример.
Свойства, конкретное значение - 5, (2,60,255), легкий, мокрый, красный.
Признак, обобщение свойств, объект, понятие, как пересечение признаков - стол, яблоко, Z, Float X, Coloreff Q
Утверждение, описание понятия, простейшая конструкция «признак это свойства», «это», конструкция, в которой присутствует знак «:=», - x := 5
Утверждение, «это», «пусть», частный вид суждения, явное выражение, функция, содержит переменные и действия (операции) с ними - x := m+n/3, z:=sin(t)
Алгебраическое выражение, составленное из чисел, переменных, знаков операций (+,-,*,/). В речи формируется словами-глаголами: склеить, подарить, отдать, взять, слить, разделить – величина, меньшая величины F на m: y:=F-m.
Суждение, уравнение, причинно-следственная связь, неявная функция, два утверждения (выражения), связанные знаком «=», а также «<», «>», системы суждений в виде суждений, связанных между собой знаками И, ИЛИ, НЕ, системы уравнений, связанные знаками И, ИЛИ, НЕ, вид равновесия, закон, частный вид умозаключения - x+y=5, F=m*a, I=U/R, F(x,y,z)=0
Умозаключение, конструкция «Если…, то….», связывающая операцией импликации два и более суждений, триада, связывающая посылку, преобразование и результат. Для реализации результата требует указания правила вывода - модуса.
Алгебраическое преобразование подразумевает перенос неизвестной величины в левую часть уравнения, а известных величин – в правую для явного выражения неизвестного через известные посредством обратных операций к использованным в записи. Сводит неявное уравнение к явному выражению.
Например, «Темно», Если «темно», то «мы спим» -> «Мы спим». Использован modus ponens.
Еще пример.
4*x-5*y=2*x+y-10, y=6 -> 2*x=-10+6*y, x=-5+3*y, x=-5+3*6, x=13.
Использованы правила коммутативности, обращения операций: c=a+b -> c=b+a, a+b=c -> а=с-b, a*b=c -> a=c/b, c=a*b -> c=b*a.
Формы мышления представлены в ИИ как системы из типов мышления за счет дополнения их действиями над ними, операциями, связями, глаголами.
Законченное понятие, утверждение, суждение, умозаключение является системой (мыслью) и снова может быть обозначено образом в виде знака или символа.
Абстрактная мысль (идея) - это предельно обобщенный образ предмета.
Знаком является изображение (жест, действие), под которым подразумевается какая-либо конкретная мысль.
Символ – это вещь, изображение или иное, чему присваивается особый глубокий смысл, лишь косвенно связанный с непосредственным содержанием видимого.
Знаки чаще образуют целые системы. Символы, как правило, «предпочитают» обособленное существование. Знак обычно незамысловат. Чем проще он расшифровывается, тем удобней пользоваться таким средством. Символ, напротив, богат по своему содержанию. Это некая загадка, для понимания которой нужно уметь размышлять. Кроме того, символ, в противоположность знаку, может толковаться в нескольких вариантах. Например, зеленый цвет связывается с умиротворением, спокойствием, гармонией, свежестью, юностью, обновлением. Иногда бывает трудно догадаться, как истолковывается тот или иной знак, – это следует просто выяснить и запомнить. Но в любом случае подобные изображения очень конкретны. Часто знаки что-то разрешают, запрещают или являются предупреждающими.
Символ же служит обнаружению того, что не лежит на поверхности. Он не указывает прямо на какой-либо предмет, а представляет собой абстракцию. Здесь ключевую роль играет художественный образ, олицетворяющий идею, переживание или, к примеру, представление о профессии, направлении искусства. Символизировать что-то могут цвета (белый – невинность), фигуры (круг – вечность), изображения животных (лев – сила, величие). Герб и флаг – это тоже символы. Отличие знака от символа состоит, в первую очередь, в соотношении зрительного образа и того, что под ним скрывается. Знак прямо указывает на что-то. Например, палец у сомкнутых губ явно выражает просьбу сохранять молчание, а глядя на изображение перечеркнутого утюга на этикетке, каждый поймет, что гладить такую вещь нельзя.
Опережая дальнейшее изложение, сообщу, что мысль – представляется законченным предложением. Впервые мысль появляется на 5 уровне языка и соответствует суждению.
Примечание. Бесконечный мир наш конечный мозг может вместить в себя при условии, что он сожмет (упростит) бесконечное число бесконечно разнообразных экземпляров в конечное число конечных кластеров (понятия), обобщив индивидуальности экземпляров насколько это возможно без большого нарушения смысла. Кластеризация (классификация) – способ познания бесконечного мира за конечное время, попытка свести бесконечность к конечности. «Модель – бесконечное в конечном» (Д.И. Менделеев).
|
|
| Рисунок – Отражение бесконечного мира (размытые нечеткие границы) в модель мира в интеллектуальной системе (четкая рамка) |
Очевидно, что при разбиении на классы при образовании понятий возникает задача рационального определения границ разбиения. Такая граница характеризуется количеством классов и количеством конкретных объектов внутри классов. Плохо, когда классов слишком мало, но в классах очень много разнородных объектов. Но также плохо, когда классов слишком много, но в каждом классе очень мало объектов.
Задача решается отслеживанием кривой суммарной ошибки отнесения объектов к классу (расстояние от объекта до центра множества объектов класса) в зависимости от количества классов. Дополнительное разбиение на подклассы имеет смысл остановить, если приращение (выгода от разбиения на большее количество классов) ошибки становится меньше, чем число е. Наглядно такое разбиение можно отобразить в виде кластеров, входящих друг в друга.
Кластер – относительно плотное множество из предметов по сравнению с другими областями пространства признаков. Класс и кластер – практически одно и тоже. Иногда используют название таксон.
Кластерный анализ – метод группировки совокупности объектов по значениям признаков для получения нескольких более или менее однородных плотных групп, четко отличающихся друг от друга, распределение объектов по классам.
Кластерный анализ придает количественную меру основному приему искусственного интеллекта – «сходство-различие». Измерив «сходство-различие», кластерный анализ позволяет выбирать и упорядочивать предметы по параметру сходства.
Из всего сказанного ясно, что для кластерного анализа необходимо определить:
- пространство признаков (осей координат),
- предметы, как точки этого пространства (экземпляры), экземпляры обладают свойствами (конкретными числовыми значениями признаков на осях координат),
- метрику – способ измерения расстояния между двумя предметами в пространстве (сходства-различия),
- критерий (правило принятия решения) объединения предметов в класс по метрике.
Результатом кластерного анализа является дерево последовательного укрупнения классов, то есть вхождения одних классов в другие, вычисление взаимоотношений между понятиями «род-вид» на количественной основе.
|
|
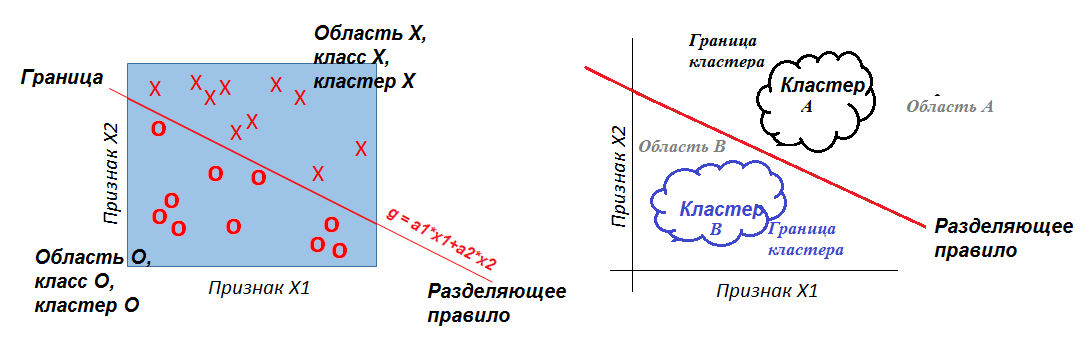
| Рисунок – Разбиение объектов (точек) на области (классы) разделяющим правилом (поверхность, линия, заданная уравнением) в пространстве признаков (системы координат) |
Для анализа следует задать {х1, х2, х3, …, хn} – объекты (предметы), каждый из которых имеет Р признаков (a, b, c, d, …). Часто объекты заданы как записи базы данных с полями в виде признаков.
Таблица – База данных объектов, характеризующихся признаками
| a (вес) | b (рост) | с (возраст) | d (образование) | e (адрес) | |
| Иванов | 100 | 177 | 35 | Высшее | И-12-15 |
| Кошкин | 57 | 160 | 45 | Среднее | А-02-10 |
| Мышкин | 83 | 190 | 24 | Среднее | Р-13-100 |
| Ложкин | 62 | 172 | 30 | Высшее | А-02-12 |
Обозначим как R (хi, хj) – расстояние между объектами i и j.
Объект – вектор свойств-признаков.
Чтобы сравнение было корректным, необходимо выполнение трех условий:
- R (хi, хj) = 0 тогда и только тогда, когда хi = хj
- R (хi, хj) = R (хj, хi) - рефлексивность
- R (хi, хj) <= R (хi, хk) + R (хk, хj) - транзитивность
Если признаки у объектов измерены в различных единицах, то надо нормировать значения признаков по одной из формул, основной из которых является формула масштабирования:
Y = (x - xmin)/(xmax - xmin)
Далее следует выбрать метрику.
Известны Евклидова метрика, метрика Минковского, метрика Чебышева, Хеммингово расстояние, метрика Пирсона.
Евклидова метрика: R(xi,xj) = √((xai - xaj)2 + (xbi - xbj)2).
|
|
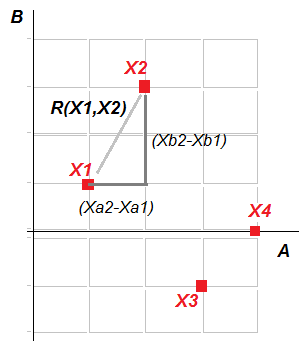
| Рисунок – Пример применения Евклидовой метрики. Расстояние R между Х1 и Х2 равно √5 |
Далее следует выбрать меру сходства классов, содержащих в себе множество объектов. Во время слияния нескольких объектов в один класс возникает проблема вычисления расстояния между классами, которые имеют размытые границы.
Перечислим известные меры расстояния между классами:
- правило ближайшего соседа - расстояние между кластерами определяется как расстояние между двумя наиболее близкими объектами в различных кластерах;
|
|
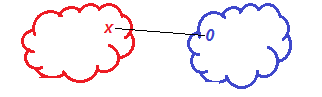
| Рисунок – Правило ближайшего соседа: R(Sl,Sm) = min(R(Xi,Xj)) |
- правило дальнего соседа - расстояние между кластерами определяется как расстояние между двумя наиболее далекими объектами в различных кластерах;
|
|
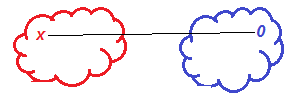
| Рисунок – Правило дальнего соседа: R(Sl,Sm) = max(R(Xi,Xj)) |
- по центрам тяжести классов;
|
|
| Рисунок – Правило центра классов: R(Sl,Sm) = ЦТ(R(Xi,Xj)) |
- по средней связи.
|
|
| Рисунок – Правило средней связи: R(Sl,Sm) = ∑∑(R(Xi,Xj))/(Nl*Nm) |
- обобщенное расстояние (по А.Н. Колмогорову)
R(Sl,Sm) = {∑∑(Rt (Xi,Xj))/(Nl*Nm)}1/t.
При t->∞ формула Колмогорова дает формулу дальнего соседа, а при t->-∞ соответствует формуле ближнего соседа, при t=2 имеем формулу Евклидового расстояния.
Существует общая формула для пересчета расстояния между заданным классом Sl и классом, который объединяет два класса Sm и Sq.
R(Sl, Smq) = a*Rlm + b*Rlq + d*Rmq +c*abs(Rlm - Rlq)
- Если a = b = -c = 0.5, d = 0, то это соответствует правилу «ближнего соседа».
- Если a = b = c = 0.5, d = 0, то это соответствует правилу «дальнего соседа».
- Если a = Nm/(Nm + Nq), b = Nq/(Nm + Nq), c = d = 0, то это соответствует правилу «средней связи». N – число элементов в соответствующих кластерах.
Рассмотрим пример.
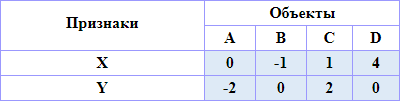
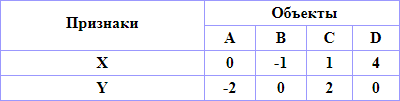
4 объекта {A, B, C, D}, 2 признака (x, y). Примем правило «ближайшего соседа» для сравнения классов. Для сравнения объектов примем Евклидову метрику. Примем исходные данные в следующем виде:
|
|
|
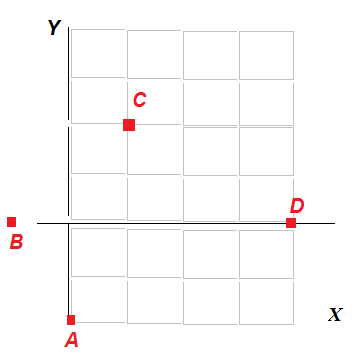
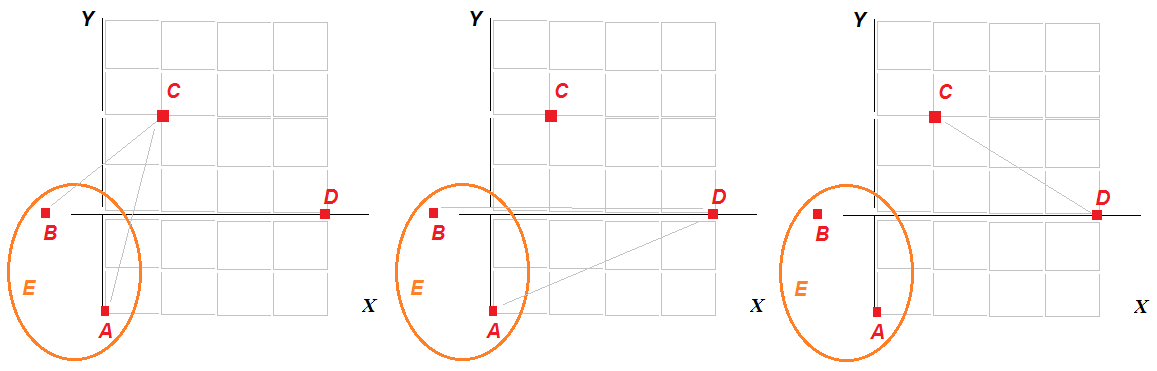
| Рисунок – Расположение объектов A, B, C, D в пространстве признаков X и Y |
Шаг 1.
Вычислим для примера расстояние между объектами А и В:
R(A, B) = (0 – (-1))2 + (-2-0)2 = 5
(Использована почти Евклидова метрика. Так как подкоренное выражение растет монотонно, также как корень из этого выражения, то можно не вычислять корень, сэкономив на вычислениях. Для сравнения величин на «больше-меньше» этого достаточно).
Аналогично вычисляем расстояния между всеми парами объектов и сводим их в матрицу расстояний R:
| A | B | C | D | |
| A | 0 | 5 | 17 | 20 |
| B | 5 | 0 | 8 | 25 |
| C | 17 | 8 | 0 | 13 |
| D | 20 | 25 | 13 | 0 |
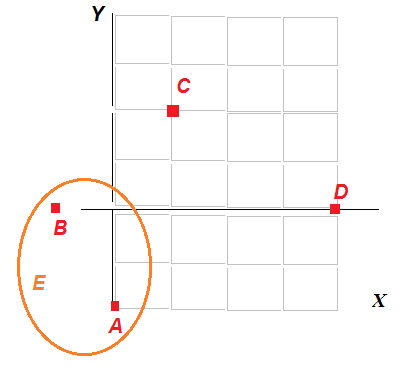
Используя правило «ближайшего соседа», находим, что ближайшими соседями являются объекты А и В, так как самое маленькое число в матрице – 5. Поэтому объединяем объекты А и В в один Е.
В результате получаем матрицу данных в виде:
|
|
|
| Рисунок – Объединение объектов A и B в единый кластер Е |
Шаг 2.
Рассчитаем расстояния между кластерами и объектами правилом ближайшего соседа:
R(E, C) = min(R (А, С), R(В, С)) = min(17, 8) = 8
R(E, D) = min(R (А, D), R(В, D)) = min(20, 25) = 20
R(C, D) = 13
|
|
| Рисунок – Измерение расстояний от кластера Е = {A, B} до объектов С и D |
Сведем результаты в матрицу расстояний между классами E, C, D:
| E | C | D | |
| E | 0 | 8 | 20 |
| C | 8 | 0 | 13 |
| D | 20 | 13 | 0 |
Тоже самое можно получить, применив для расчета между кластерами формулу Колмогорова в варианте «ближайшего соседа»:
R(Sl, Smq) = a*Rlm + b*Rlq + d*Rmq + с*abs(Rlm - Rlq)
Для вычисления расстояния между Е и С.
Роль l играет класс С, роль m играет класс А, роль q играет класс В.
При a = b = -c = 0.5, d = 0 (правило «ближнего соседа») имеем:
R(Sl, Smq) = R(SA, Smq) = 0.5*RСA + 0.5*RСB + d*RAB - 0.5*abs(RCA - RCB) =
= 0.5*17 + 0.5*8 + 0*5 + (-0.5)*|8-17| = 8
Также вычисляем расстояния между E и D (R = 20), C и D (R = 13).
Наиболее близкие кластеры E и С, так как расстояние между ними наименьшее и равно 8. Объединяем E и С в класс F.
В результате получаем матрицу данных в виде:
|
|
|
| Рисунок – Появление кластера второго уровня F={{A, B}, C} |
Шаг 3.
Рассчитаем расстояние между кластерами.
R(F, D) = min(R(E, D), R(D, C)) = min(20, 13) = 13
Теперь матрица расстояний между классами F и D имеет вид:
| F | D | |
| F | 0 | 13 |
| D | 13 | 0 |
Объединяем F и D в один класс.
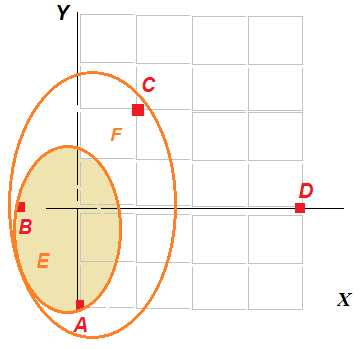
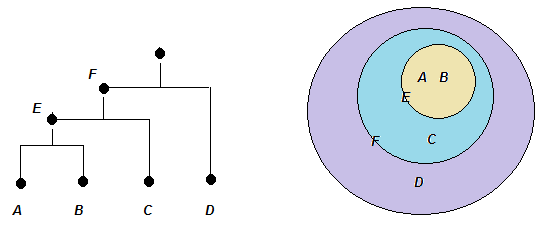
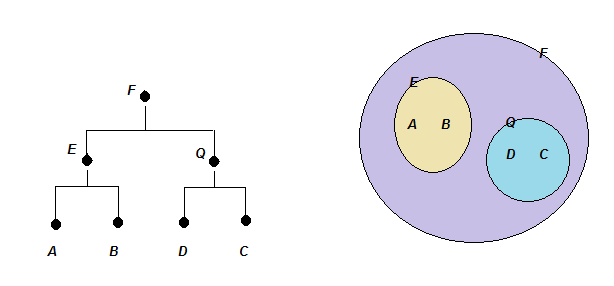
Результат кластеризации понятен из рисунка «Дерево классов».
|
|
| Рисунок – Дерево классов |
Тот же пример, рассчитанный правилом «дальнего соседа», дает несколько отличный результат кластеризации.
Исходная матрица:
|
Шаг 1.
Вычислим для примера расстояние между объектами А и В:
R(A, B) = (0 – (-1))2 + (-2-0)2 = 5
Аналогично вычисляем расстояния между всеми парами объектов и сводим их в матрицу расстояний R:
| A | B | C | D | |
| A | 0 | 5 | 17 | 20 |
| B | 5 | 0 | 8 | 25 |
| C | 17 | 8 | 0 | 13 |
| D | 20 | 25 | 13 | 0 |
Используя правило «ближнего соседа», находим, что ближайшими соседями являются объекты А и В, так как самое маленькое число в матрице – 5. Поэтому объединяем объекты А и В в один Е.
В результате получаем матрицу данных в виде:
|
Шаг 2.
Рассчитаем расстояния между кластерами правилом «дальнего соседа»:
R(E, C) = max(R(А, С), R(В, С)) = max(17, 8) = 17
R(E, D) = max(R(А, D), R(В, D)) = max(20, 25) = 25
R(C, D) = 13
Сведем результаты в матрицу расстояний между классами E, C, D:
| E={A,B} | C | D | |
| E={A,B} | 0 | 17 | 25 |
| C | 17 | 0 | 13 |
| D | 25 | 13 | 0 |
Наиболее близкие кластеры C и D, так как расстояние между ними наименьшее и равно 13. Объединяем C и D в класс Q.
В результате получаем матрицу данных в виде:
|
Шаг 3.
Рассчитаем расстояния между кластерами.
R(E, Q) = max(R(E, С), R(E, D)) = max(17, 25) = 25
Матрица расстояний имеет вид:
| E | Q | |
| E | 0 | 25 |
| Q | 25 | 0 |
Остается на последнем шаге объединить классы E и Q.
|
|
| Рисунок – Объединение объектов в классы правилом «дальнего соседа» |
В результате получаем дерево и график.
|
|
| Рисунок – Дерево классов |
Метод кластеризации «k-means»
Метод изобретен Mac-Queen в 1967 г. и позволяет определить, в какие компактные группы входят заданные экземпляры.
Метод требует указать, на сколько кластеров k требуется разбить множество объектов (точек, экземпляров). Поэтому процедуру прогоняют несколько раз, для различных исходных значений k.
Суть метода:
- 1. Задается количество кластеров k.
- 2. «Случайно» выбираются их центры.
- 3. Определяется, к какому кластеру k очередная точка (объект) ближе по выбранной нами мере. Точка переносится в соответствующий кластер. Пункт 3 повторяется для всех точек.
- 4. После того как все точки нашли своего нового «хозяина», пересчитываются центры изменившихся кластеров, например, как центры тяжести всех точек, которые содержит кластер.
- 5. Пункты 3-4 повторяются до тех пор, пока точки не перестают переходить из кластера в кластер (или центры кластеров перестают смещаться).
К недостаткам метода относят его чувствительность к ошибкам в определении положения точек, которые существенно влияют на их распределение, и необходимость исследователю самому решать, сколько кластеров k содержит распределение точек. К тому же неудачное первое распределение центров тяжести будущих кластеров может привести к отказу метода.
Рассмотрим пример.
Допустим, что производились измерения по 2 координатам продаваемой продукции: вес товара в упаковке и цена единицы упакованного товара Товаровед решил разделить эту продукцию на 2 класса, расположив ее по двум разным витринам (k = 2). Экспериментально были измерены 8 экземпляров продукции.
| Название экземпляра | Вес, x | Цена, y |
| A | 1 | 3 |
| B | 3 | 3 |
| C | 4 | 3 |
| D | 5 | 3 |
| E | 1 | 2 |
| F | 4 | 2 |
| G | 1 | 1 |
| H | 2 | 1 |
График распределения экземпляров показан на рисунке.
|
|
| Рисунок – Пример расположения точек в пространстве координат (x – вес, y - цена) |
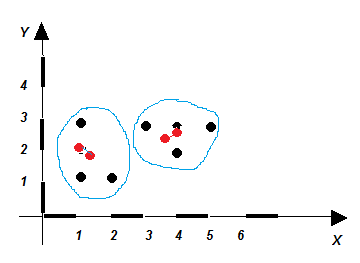
Примем случайным образом, что центры кластеров располагаются в (1, 1) и (2, 1) – обозначены на рисунке красным цветом.
|
|
| Рисунок – Экземпляры и начальное (случайное) положение центров двух классов |
Вычислим расстояния от i-той точки до каждого из этих центров. Расстояние будем измерять евклидовой мерой. Точку отнесем к тому кластеру, расстояние до которого будет меньше.
Итерация 1.
Например, точка А находится на r1 = √((1 - 1)2 + (3 - 1)2) = 2 от центра тяжести первого кластера и на расстоянии r2 = √((1 - 2)2 + (3 - 1)2) = 2.24 от второго центра тяжести. То есть точка А ближе к первому кластеру, чем ко второму (2 < 2.24), поэтому помещаем А в первый кластер. Остальные точки приведены в таблице расстояний.
| Название экземпляра, точка с координатами | r1 от точки до центра тяжести 1 (1, 1) | r2 от точки до центра тяжести 2 (2, 1) | Номер ближайшего к точке кластера k |
| A (1, 3) | 2 | 2.24 | 1 |
| B (3, 3) | 2.83 | 2.24 | 2 |
| C (4, 3) | 3.61 | 2.83 | 2 |
| D (5, 3) | 4.47 | 3.61 | 2 |
| E (1, 2) | 1 | 1.41 | 1 |
| F (4, 2) | 3.16 | 2.24 | 2 |
| G (1, 1) | 0 | 1 | 1 |
| H (2, 1) | 1 | 0 | 2 |
Минимальное расстояние min(r1, r2) выделено в таблице в каждой строке цветом. То есть в кластер 1 попадают точки {A, E, G}, а в кластер 2 - {B, C, D, F, H}.
Суммарное расстояние от точек до центров их кластеров составляет:
Е = 22 + 2.242 + 2.832 + 3.612 + 12 + 2.242 + 02 + 02 = 36
Теперь кластер 1 имеет центр тяжести в новой точке (арифметическое среднее координат входящих в него точек): ((1 + 1 + 1)/3, (3 + 2 + 1)/3) = (1, 2).
А кластер 2 имеет центр тяжести в точке (арифметическое среднее координат входящих в него точек): ((3 + 4 + 5 + 4 + 2)/5, (3 + 3 + 3 + 2 + 1)/5) = (3.6, 2.4).
То есть центры тяжести кластеров поменяли свое положение. Значит, процедуру следует продолжать. Кластеры 1 и 2 показаны на рисунке синим цветом. Красные вектора показывают смещение центров тяжести кластеров в новое положение.
|
|
| Рисунок – Пример расположения точек по кластерам на первой итерации |
Итерация 2.
Снова измерим расстояние от каждой точки до центра каждого кластера.
| Название экземпляра | r1 (1, 2) | r2 (3.6, 2.4) | Номер кластера k |
| A (1, 3) | 1 | 2.67 | 1 |
| B (3, 3) | 2.24 | 0.85 | 2 |
| C (4, 3) | 3.16 | 0.72 | 2 |
| D (5, 3) | 4.12 | 1.52 | 2 |
| E (1,2) | 0 | 2.63 | 1 |
| F (4, 2) | 3 | 0.57 | 2 |
| G (1, 1) | 1 | 2.95 | 1 |
| H (2, 1) | 1.41 | 2.13 | 1 |
Сравнивая расстояния от точки до кластера 1 и кластера 2, определим, к какому кластеру каждая точка больше тяготеет на второй итерации (в нашем случае точка Н перебежала из кластера 2 в кластер 1).
Минимальное расстояние выделено в таблице цветом. То есть в кластер 1 попадают точки {A, E, G, H}, а в кластер 2 - {B, C, D, F}.
Суммарное расстояние от точек до центров их новых кластеров составляет:
Е = 12 + 0.852 + 0.722 + 1.522 + 02 + 0.572 + 12 + 1.412 = 7,86 (расстояние по сравнению с распределением точек по кластерам на первой итерации уменьшилось, то есть распределение точек по кластерам улучшилось в 36/7,86 = 4.6 раза).
Теперь кластер 1 имеет центр тяжести в точке (арифметическое среднее координат входящих в него точек): ((1 + 1 + 1 + 2)/4, (3 + 2 + 1 + 1)/4) = (1.25, 1.75).
А кластер 2 имеет центр тяжести в точке (арифметическое среднее координат входящих в него точек): ((3 + 4 + 5 + 4)/4, (3 + 3 + 3 + 2)/4) = (4, 2.75).
То есть центры тяжести кластеров снова поменяли свое положение. Значит, процедуру следует продолжать. Кластеры 1 и 2 показаны на рисунке синим цветом. Красные вектора показывают смещение центров тяжести кластеров в новое положение.
|
|
| Рисунок – Пример расположения точек по новым кластерам на второй итерации |
Итерация 3.
Снова измерим расстояние от каждой точки до центра каждого кластера.
| Название экземпляра | r1 (1.25, 1.75) | r2 (4, 2.75) | Номер кластера k |
| A (1, 3) | 1.27 | 3.01 | 1 |
| B (3, 3) | 2.15 | 1.03 | 2 |
| C (4, 3) | 3.02 | 0.25 | 2 |
| D (5, 3) | 3.95 | 1.03 | 2 |
| E (1,2) | 0.35 | 3.09 | 1 |
| F (4, 2) | 2.76 | 0.75 | 2 |
| G (1, 1) | 0.79 | 3.47 | 1 |
| H (2, 1) | 1.06 | 2.66 | 1 |
Сравнивая расстояния от точки до кластера 1 и кластера 2, определим, к какому из новых кластеров точка больше тяготеет (в нашем случае все точки остались в старых кластерах).
Минимальное расстояние выделено в таблице цветом: кластер 1 - точки {A, E, G, H}, кластер 2 - {B, C, D, F}.
Суммарное расстояние от точек до центров их кластеров составляет:
Е = 1.272 + 1.032 + 0.252 + 1.032 + 0.352 + 0.752 + 0.792 + 1.062 = 6,23 (расстояние уменьшилось, то есть распределение точек по кластерам улучшилось в 7,86/6,23 = 1.26 раза).
Центры тяжести кластеров не поменялись, так как не изменилось распределение точек по кластерам. Процедура кластеризации останавливается.
Ответ: кластер 1 - точки {A, E, G, H}, кластер 2 - {B, C, D, F}.
Примечание.
Процедуру следует провести при различных значениях k = 2, 3, 4, т.д..
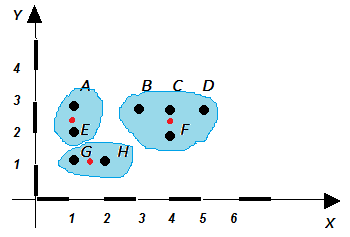
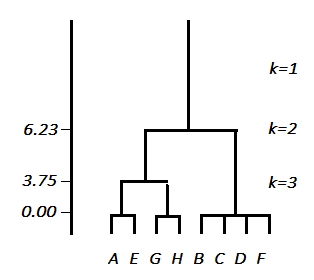
На рисунке показано дальнейшее разбиение исходного множества на кластеры (k = 3). Суммарная ошибка распределения точек по кластерам Е составит при этом 3.75.
|
|
| Рисунок – Разбиение исходного множества на k = 3 |
|
|
| Рисунок – Дерево классов |
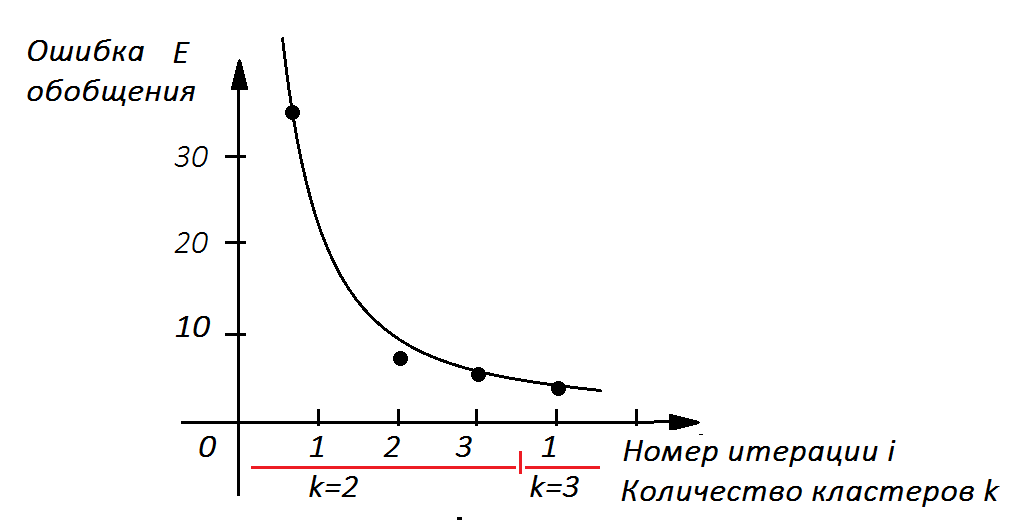
Если ошибка Е с ростом очередного значения k меняется незначительно, то дальнейшее разбиение исходного множества экземпляров на все более мелкие кластеры не имеет особого смысла.
|
|
| Рисунок – Пример графика характерной зависимости ошибки E разнесения объектов по классам от номера итерации i метода k-means и количества кластеров k |
Внимание!
В зависимости от комбинации принятых за основу исходных принципов кластеризации, исходных и начальных данных могут получаться различные решения задачи кластеризации (или вовсе не получаться). Для примера можете поэкспериментировать со структурами, изображенными ниже, пытаясь разбить множество точек на кластеры.
|
То, что очевидно для человеческого взгляда, метод может не распознать.
Задание
Задаться примером для метода k-means (не менее 3D, не менее 15 экземпляров). Например, задаться количеством признаков, достаточным для отличия кошек от собак и различения их по видам.
Провести кластеризацию множества экземпляров для случаев: k=2, k=3, k=4. Нарисовать дерево классов. Привести графическую иллюстрацию. Привести функцию суммарной ошибки E(k).
Метод «Cos» (метод О.И.Мухина, 2019 г.)
Сравнение объектов. Похожесть. Объекты и группы
Методы классификации помогают нам определить, насколько два сложных объекта похожи друг на друга - какие объекты следует отнести к одной группе, а какие к другой. Возьмем, например, такие объекты, как яблоко, арбуз, киви, груша, тыква, кабачок, помидор, забор. Как и по каким группам их распределить, в какую группу попадут одни объекты, а в какую – другие?
В современных информационных системах анализируют, какие люди покупают какие товары.
Например, Вы купили в интернет-магазине садовую тележку, кусторез и лопату. На основании анализа купленных Вами товаров система определит, к какому классу покупателей Вы относитесь, видимо, «садовод». Разумеется, задолго до этого система, автоматически анализируя потоки покупок, выявляет группы похожих покупателей (строит модель).
Далее система предложит Вам купить дополнительные товары из списка, обычно покупаемых садоводами (строит по модели прогноз, решая задачу с Вашими исходными данными, отвечая на вопрос «Что бы Вам такое предложить, чтобы Вам захотелось купить?»). Возможно, что это будет книга по садоводству, но вряд ли телескоп или горчичник. В огромном мире современных товаров, где за внимание покупателя надо бороться, решение такой задачи для продавца является крайне важным.
Интересна и важна другая задача - какие два из тысячи разных объектов больше всего похожи друг на друга.
Например, люди могут быть охарактеризованы сотней признаков (трудолюбие, любознательность, активность, коммуникабельность, упорство и так далее). Какие два человека могут заменить друг друга? Кто из людей больше всего подходит для выполнения определенной работы? Какие типы людей в дефиците в конкретной организации, а какие качества встречаются у людей чаще всего? Какие качества заменяют друг друга, а какие – нет? Какие качества у людей можно назвать базовыми, основными, а какие только определяются через базовые и на сколько?
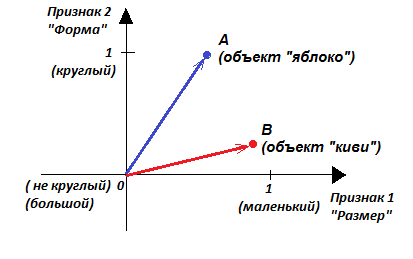
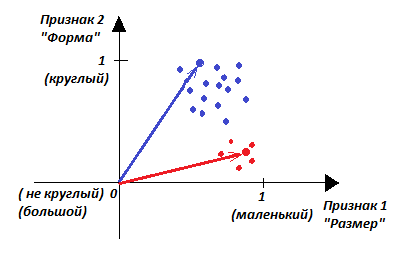
Итак, допустим, что у нас есть объекты A и B, каждый из которых характеризуется двумя признаками (x, y). Например, объект A – яблоко со свойствами: средний размер, круглая форма. Обозначим первый признак «Размер» как x, второй признак «Форма» как y. Тогда яблоко можно обозначить как А(x, y) = А(средний, круглая). Если договориться, что значение 1 признак «Размер» принимает у маленьких объектов, а значение 0 этот же признак принимает у больших объектов, то для конкретного среднего яблока можно принять x = 0.5. Если договориться, что значение 1 признак «Форма» принимает у круглых объектов, а значение 0 этот признак принимает у некруглых объектов, то для конкретного круглого яблока можно принять y = 1.
То есть яблоко – это А(0.5, 1.0). На рисунке объект А представлен синей точкой в координатах (x, y).
|
|
| Рисунок – Распределение фруктов по размеру и форме (пример) |
В этих же осях изобразим другой объект «киви» красной точкой. Объект В – киви со свойствами (x = почти маленький, y = овал, но не квадрат). Например, конкретный киви B(0.95, 0.3).
То есть, если мы имеем два объекта, то они могут быть представлены как две точки в системе координат, заданной описываемыми признаками. Каждый признак – это отдельная ось координат, значение признака (то есть свойство) – точка на этой оси.
Насколько похожи эти объекты с точки зрения начала координат, где находится наблюдатель, может показать геометрический анализ. Если дополнительно к системе объектов принять еще и точку зрения О, то объекты будут характеризоваться векторами. В нашем случае OA и OB.
Мерой сходства-различия двух объектов может служить косинус угла между векторами, направленными на эти точки из начала координат. Измеряя угол, мы можем оценить сходство объектов. Подсчитать угол в геометрии удобнее всего по формуле косинуса.
Косинус равен нулю, если вектора перпендикулярны, угол между векторами равен 90 град. или -90 град.. Это означает, что объекты непохожи между собой, абсолютно различны. Свойства объектов перпендикулярны!
Косинус равен единице (максимальное число), если вектора параллельны, угол между векторами равен 0 град. (вектора сонаправлены). Это означает, что объекты имеют максимальное сходство.
Косинус равен минус единице (минимальное число), если вектора параллельны, но противоположны, угол между векторами равен 180 град. или -180 град. (направления векторов противоположны). Это означает, что объекты антиподы. Сходство их выражено в зеркальной симметрии.
То есть логично считать, что косинус будет удобной для нас мерой схожести: 1 – объекты максимально схожи, 0 – объекты непохожи, (-1) – объекты максимально различны.
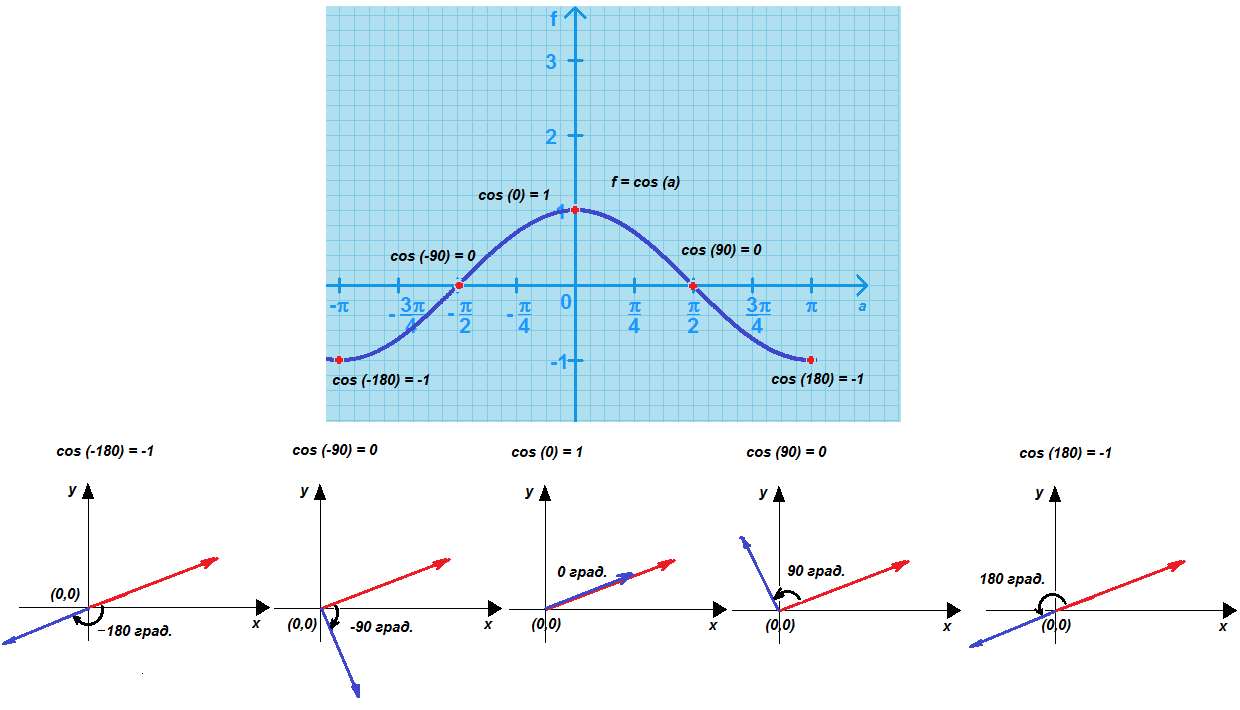
На рисунке показан график косинуса угла а с его значениями f(α) и соответствующие примеры различного расположения объектов двух А и В в осях (x, y).
Напомним, что угол измеряют как в градусной, так и в радианной мере. Соотношение между мерами: 0 градусов – 0 радиан, 180 градусов – π радиан. То есть переход от градусов к радианам можно осуществить по формуле пропорции:
а(рад) = а(град) * π/180,
где π = 3.14… (с точностью до двух знаков после запятой).
|
|
| Рисунок – Косинус угла между направлениями взгляда наблюдателя на сравниваемые объекты как мера схожести двух объектов |
На рисунке яблоко и киви по данным признакам похожи друг на друга на 0,445, так как угол между векторами, смотрящими на эти объекты из точки наблюдения (0, 0), составляет 63 градуса. То есть, сходство у этих объектов есть (по данным признакам!), хотя и неполное.
Ясно, что яблоки бывают разные: и побольше, и поменьше, а также как круглые, так и не совсем круглые (разумеется, вместо «круглый» более правильно говорить «шарообразный»). Киви тоже не все похожи абсолютно друг на друга, их форма и размер имеют отличия, разброс. Этот факт отображен на рисунке множеством точек, каждая из которых обозначает конкретный экземпляр фрукта.
|
|
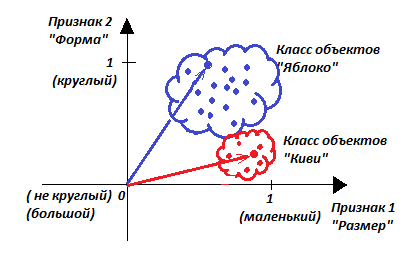
| Рисунок – Пример разброса экземпляров двух классов в пространстве признаков |
Однако, несмотря на различия, разные экземпляры киви геометрически находятся друг рядом с другом, составляя «облако», поскольку сходства разные экземпляры киви имеют больше, чем различия. Все вместе они составляют класс «Киви».
Тоже рассуждение можно отнести и к яблокам. На рисунке показаны два разных класса: класс «яблоки» и класс «киви», состоящие из конкретных экземпляров. Чем более компактны множества, тем меньше разнообразия у конкретных фруктов.
|
|
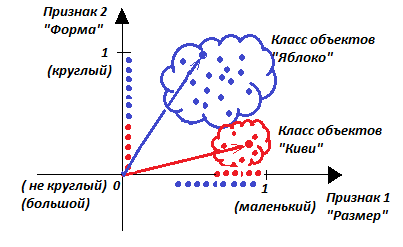
| Рисунок – Пример расположения двух классов в пространстве признаков |
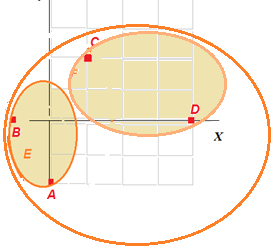
Заметим, что если по каким-то признакам разные классы имеют сходство, то классы или их проекции на оси могут пересекаться. Например, и киви, и яблоки бывают маленькие – на рисунке проекция множества яблок и проекция множества киви на ось признака «Размер» пересекаются. А вот их проекции на ось «Форма» - нет. Поэтому яблоки от киви лучше отличать по форме, а не по размеру.
|
Хотя, будем справедливы, на оси «Форма» классы в нашем случае находятся тоже довольно близко, так, что их проекции почти касаются краями. Стоит найтись совсем странному яблоку, как оно будет ошибочно отнесено к киви.
В этом случае надо проводить дополнительные оси, чтобы четко отличить один класс от другого. Достаточно ввести ось «Цвет», чтобы отличить коричневое киви от зеленых, красных, желтых яблок.
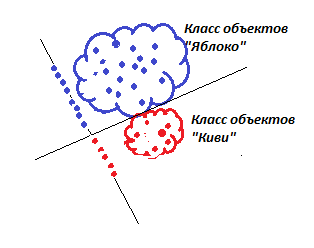
Другой вариант решения проблемы показан на рисунке. Достаточно провести самим оси «Размер-Форма» под другим углом, чтобы два класса стали отличаться друг от друга.
|
|
| Рисунок – Поворот осей в системе «Форма-Размер» для лучшего разделения классов |
Разумеется, главная ось, на которой отчетливо будет видно отличие яблок от киви, будет уже называться по-другому: «Формо-размер». Еще точнее, «8*Форма = 3*Размер» или 8y - 3x = 0. Для определения «что это за фрукт» достаточно взять пропорцию 8 к 3 от значений его формы и размера.
Все сказанное легко вычислить геометрически и, зная формулы, применить для более сложных и общих случаев, например, множества объектов, множества признаков и множества классов.
Как известно, косинус угла α вычисляется через скалярное произведение векторов. Формула вычисления косинуса для трех объектов (A, B, C) и трех признаков (x, y, z) имеет вид:
cos(α) = (Ax*Bx*Cx + Ay*By*Cy + Az*Bz*Cz) / √((Ax*Ax + Ay*Ay + Az*Az)*(Bx*Bx + By*By + Bz*Bz)*(Cx*Cx + Cy*Cy + Cz*Cz)).
Задача
В бункере «Сырьё» находятся предметы (яблоки, арбузы, дыни и т.д.), которые по их мере поступления сортировочная машина (мотор, шестерня, вал, лопатка) должна разложить по отдельным ящикам (классам). Для этого нужны датчики Д1, Д2, … (формы, вкуса, цвета и т.д.) и система управления, которая должна распознавать образы предметов, которые ей посылают датчики и дать соответствующий сигнал сортировочной машине. Образ предмета состоит из набора нескольких сигналов, например, <Форма=0, Вкус=1, Цвет=1>, и называется синдромом объекта.
|
|
| Рисунок – Техническое устройство «Сортировальная машина» |
Решение
Дана таблица исходных данных.
Взяты арбуз, яблоко, огурец, дыня, забор и помидор, которые отличаются и похожи признаками: цвет, вкус, форма, размер, способ размножения.
Обратите внимание, для оценки объектов необходимо задать количественную шкалу признака. Признак – это переменная, принимающая различные числовые значения, обозначается буквой. Конкретное значение признака – свойство - выражается числом.
Например. Вес может принимать разные значения. Есть легкие предметы, а есть тяжелые. Легкий, тяжелый – конкретные свойства (числовые значения) признака Вес.
Если обозначить вес переменной (буквой) V, то, например, V:=3 будет соответствовать легкому предмету, а V:=1000 будет соответствовать тяжелому. Признак – это переменная (обозначается буквой), а свойство – значение переменной (обозначается числом). Алгебра преобразует выражения с признаками (исчисление буквенных выражений). Арифметика работает со свойствами (вычисление числовых выражений).
Красный, зеленый, синий, коричневый – конкретные свойства признака Цвет. И так далее.
Шкалу задают нулем (точка) и единицей (отрезок) или двумя точками по краям шкалы: max и min. Например, сладкое – НЕ сладкое, маленькое – большое, и так далее.
| Признак | Цвет (Ц) | Вкус (В) | Форма (Ф) | Размер (Р) | Способ размножения (С) |
| Свойство | Зеленое – Не зеленое | Сладкое - Не сладкое | Круглое - Не круглое | Маленькое – Большое | Семечки – Не семечки |
Итак.
| Признак | Цвет (Ц) | Вкус (В) | Форма (Ф) | Размер (Р) | Способ размножения (С) |
| Свойство | 1-зеленое | 1-сладкое | 1-круглое | 1-маленькое | 1-семечки |
| Яблоко (Я) | 1 | 1 | 1 | 1 | 1 |
| Арбуз (А) | 1 | 1 | 1 | 0 | 1 |
| Огурец (О) | 1 | 0 | 0 | 1 | 1 |
| Дыня (Д) | 0 | 1 | 1 | 0 | 1 |
| Забор (З) | 1 | 0 | 0 | 0 | 0 |
| Помидор (П) | 0 | 0 | 1 | 1 | 1 |
Для краткости математической записи обозначим: пространство признаков {Ц, В, Ф, Р, С}, объекты: {Я, А, О, Д, З, П}.
Похожесть яблока и арбуза определим как: cos(Я, А) = (Яц*Ац + Яв*Ав + Яф*Аф + Яр*Ар + Яс*Ас)/ √((Яц*Яц + Яв*Яв + Яф*Яф + Яр*Яр + Яс*Яс)*(Aц*Aц + Aв*Aв + Aф*Aф + Ар*Ар + Ас*Ас)) = (1*1 + 1*1 + 1*1 + 1*0 + 1*1)/√((1*1 + 1*1 + 1*1 + 1*1 + 1*1)*(1*1 + 1*1 + 1*1 + 0*0 + 1*1)) = 4/√ (5*4) = 0.9, формула показывает высокую схожесть яблока и арбуза, что соответствует углу 27 градусов между векторами, направленными из начала координат (0,0,0,0,0) к каждому из объектов.
Шаг 1. «Определение похожести пар объектов»
Подставляя соответствующие значения признаков для разных пар объектов, определим аналогично их схожесть между собой. Результаты сравнений представлены в таблице.
| Яблоко (Я) | Арбуз (А) | Огурец (О) | Дыня (Д) | Забор (З) | Помидор (П) | |
| Яблоко (Я) | 1 | 0.9 | 0.8 | 0.8 | 0.45 | 0.8 |
| Арбуз (А) | 0.9 | 1 | 0.6 | 0.87 | 0.6 | 0.7 |
| Огурец (О) | 0.8 | 0.6 | 1 | 0.3 | 0.6 | 0.7 |
| Дыня (Д) | 0.8 | 0.87 | 0.3 | 1 | 0 | 0.8 |
| Забор (З) | 0.45 | 0.6 | 0.6 | 0 | 1 | 0 |
| Помидор (П) | 0.8 | 0.7 | 0.7 | 0.8 | 0 | 1 |
Самыми похожими, исходя из таблицы, признаются Арбуз и Яблоко, степень похожести которых максимальна и равна 0,9. Объединяем Арбуз и Яблоко в один класс «АЯ».
Шаг 2. «Определение похожести троек объектов»
Сравним класс АЯ по отдельности с каждым оставшимся объектом из множества {Д,О,З,П}. Для этого вычислим четыре косинуса для троек {АЯД, АЯО, АЯЗ, АЯП}.
Например, для АЯП степень похожести равна:cos(Арбуз, Яблоко, Помидор) = (1*1*0 + 1*1*0 + 1*1*1 + 0*1*1 + 1*1*1)/√((1*1 + 1*1 + 1*1 + 0*0 + 1*1)*(1*1 + 1*1 + 1*1 + 1*1 + 1*1)*(0*0 + 0*0 + 1*1 + 1*1 + 1*1)) = 2/√(4*5*3) = 0,26
Используя далее формулу косинуса для остальных троек, имеем:
cos(Арбуз, Яблоко, Дыня) = 0,39
cos(Арбуз, Яблоко, Забор) = 0,22
cos(Арбуз, Яблоко, Огурец) = 0.26
Таким образом, больше всего похоже на класс «АЯ» объект Дыня (0,39). Объединяем АЯ с Д в один класс АЯД.
Примечание. Для общности решения можно проверить, все возможные тройки на похожесть, а не только тройки с АЯ, и найти самые схожие между собой три объекта. Но следует иметь в виду, что в пространствах высокой размерности это приведет к резкому увеличению числа вычислений.
Шаг 3. «Определение похожести четверок объектов»
Сравним класс АЯД по отдельности с каждым оставшимся объектом из множества {О, З, П}. Для этого вычислим три косинуса для четверок {АЯДО, АЯДЗ, АЯДП}.
Например, для АЯДО степень похожести равна:
cos(Арбуз, Яблоко, Дыня, Огурец) = (1*1*1*0 + 1*1*0*1 + 1*1*0*1 + 1*0*1*0 + 1*1*1*1)/√((1*1 + 1*1 + 1*1 + 0*0 + 1*1)*(1*1 + 1*1 + 1*1 + 1*1 + 1*1)*(0*0 + 1*1 + 1*1 + 0*0 + 1*1)*(1*1 + 0*0 + 0*0 + 1*1 + 1*1)) = 1/√(4*5*3*3) = 0,07
Используя далее формулу косинуса для остальных четверок, имеем:
cos(Арбуз, Яблоко, Дыня, Забор) = 0
cos(Арбуз, Яблоко, Дыня, Помидор) = 0.14
Таким образом, больше всего похож на класс «АЯД» объект Помидор (0,14). Объединяем АЯД с П в один класс АЯДП.
Шаг 4. «Определение похожести пяти объектов»
Сравним класс АЯДП по отдельности с каждым оставшимся объектом из множества {О, З}. Для этого вычислим два косинуса для пятерок {АЯДПО, АЯДПЗ}.
Например, для АЯДПО степень похожести равна:
cos(Арбуз,Яблоко,Дыня,Помидор,Огурец) = (1*1*0*0*1 + 1*1*1*0*0 + 1*1*1*1*0 + 1*1*1*1*0 + 1*1*1*1*1)/√((1*1 + 1*1 + 1*1 + 0*0 + 1*1)*(1*1 + 1*1 + 1*1 + 1*1 + 1*1)*(0*0 + 1*1 + 1*1 + 0*0 + 1*1)*(0*0 + 0*0 + 1*1 + 1*1 + 1*1)*(1*1 + 0*0 + 0*0 + 1*1 + 1*1)) = 1/√(4*5*3*3*3) = 0,04
Используя далее формулу косинуса для оставшейся пятерки, имеем:
cos(Арбуз, Яблоко, Дыня, Помидор, Забор) = 0
Таким образом, больше всего похож на класс «АЯДП» объект Огурец на уровне 0,04. Объединяем АЯДП с О в один класс АЯДПО.
Шаг 5. «Определение похожести шести объектов»
Очевидно, что АЯДПО объединяется на последнем шаге с З.
Нарисуем получившееся дерево классов: А-Я(0.9)-Д(0,39)-П(0,14)-О(0.04)-З(0).
|
|
| Рисунок – Дерево классов |
Примечание 1. Если сравнивается сразу множество объектов, то один из них может стать началом координат и расположиться там, где находится наблюдатель, с точки зрения которого формируется суждение о похожести объектов. В нашем примере наблюдатель находился в точке (0,0). За начало координат можно также принять центр тяжести какого-либо класса объектов или центр тяжести всех рассматриваемых объектов.
От выбора начала координат существенно зависит результат. Так, например, искусственно удаленный центр дает нам вид на множество объектов, как бы сосредоточенных в одной (далекой от нас, но компактной) области. На наш взгляд такие объекты будут весьма похожи друг на друга, как объекты, которые мы наблюдаем издалека. Вряд ли с расстояния 1 км вы поймете по фигуре человека его возраст, мужчина он или женщина – все фигуры будут казаться вам одинаковыми.
Перенос начала координат в область между объектами дает нам возможность считать часть объектов, которая окажется в одной стороне, одним классом, а другую часть, в другой стороне, - другим классом. В нашем примере, мужчины – слева, женщины – справа. Мы видим ситуацию более детально, находим больше различий.
Положение начала координат - это точка зрения.
Примечание 2. Мы брали значения свойств из множества 0 или 1. Результат нашей работы будет намного точнее, если значения признаков будут дробными числами (между 0 и 1), исходя из пропорции присутствия того или иного свойства в объекте. Например, яблоко не всегда бывает только размером 1, как в нашем примере.
Для другого примера за максимальный размер был взят Арбуз с присвоением ему значения размера 0. Если в крупном магазине измерить размеры у пяти попавшихся на глаза яблок, то окажется, что яблоки бывают 0,3; 0,2; 0,33; 0,24; 0,05 от размера арбуза. В среднем размер яблока в магазине оказался равен 0,224. Чем больше яблок будет перемерено, тем точнее будет результат.
Нахождение осей координат. Определение размерности пространства
Чтобы нарисовать множество объектов (в нашем примере их 6) в осях признаков (в нашем примере их 5) наиболее удачно, вычислим самые независимые друг от друга оси. Такие оси изображаются перпендикулярно друг другу и называются ортогональными. Не трудно сообразить, что самые удачные признаки для классификации (то есть для различения объектов друг от друга) – независимые, то есть те, косинус угла между которыми равен или близок к нулю.
Кстати, нам давно уже пора заняться самим пространством. Не факт, что само пространство, где располагаются объекты, 5-мерно (цвет, вкус, форма, размер, способ размножения). Возможно, что какие-то признаки зависимы от других, а их количество избыточно.
Например, все красные фрукты всегда еще и сладкие, за редким исключением. Тогда не имеет смысла держать в базе данных такой атрибут как «цвет», если в базе данных есть уже атрибут «вкус». А зная вкус, можно вычислить с определенной точностью цвет экземпляра.
Итак, надо научиться определять размерность пространства.
Не факт, что оси (признаки) в нашем примере располагаются под прямым углом, т.е. независимы, а само пространство линейно.
Если спроецировать все объекты на каждую из осей по-отдельности, то можно увидеть, что лучше всего объекты разделяются по признакам: Вкус, Размер.
Оси делят все объекты на две одинаковые крупные части, на два класса. Вкус делит объекты на сладкие и несладкие, а Размер делит объекты на крупные и мелкие. Далее идут Цвет и Форма, они делят объекты на 2 класса по 2 и 4 объекта в каждом. Последним идет Способ, который делит объекты на 2 класса по 1 и 5 объектов в каждом.
Отсюда следует, что наиболее информативными являются признаки Вкус и Размер, именно они лучше всего дифференцируют (разделяют) множество объектов примера.
|
Вычислить в сложных случаях распределений степень дифференциации можно по формуле энтропии (информации), которую нам предоставляет информатика:
i = - 1/n1*lg2(1/n1) - 1/n2*lg2(1/n2) (формула Шеннона).
Выбирая самый информативный признак max (iв, iр, iц, iф, iс), получаем iв = iр = 1. Такими признаками в нашем примере оказались Вкус и Размер, поэтому в первую очередь для классификации надо попытаться использовать именно их.
Вычислим теперь для нашего примера углы между осями (признаками). Используем для этого формулу косинуса, беря все возможные пары.
Например, косинус угла между Цветом и Вкусом:
сos(Ц, В) = (1*1 + 1*1 + 1*0 + 0*1 + 1*0 + 0*0)/√((1*1 + 1*1 + 1*1 + 0*0 + 1*1 + 0*0)*(1*1 + 1*1 + 0*0 + 1*1 + 0*0 + 0*0)) = 2/√(4*3) = 0,58
Подсчитав аналогично остальные углы, имеем:
| Признак | Цвет (Ц) | Вкус (В) | Форма (Ф) | Размер (Р) | Способ размножения (С) |
| Цвет (Ц) | 1 | 0.58 | 0.5 | 0.58 | 0.77 |
| Вкус (В) | 0.58 | 1 | 0.87 | 0.33 | 0.77 |
| Форма (Ф) | 0.5 | 0.87 | 1 | 0.58 | 0.9 |
| Размер (Р) | 0.58 | 0.33 | 0.58 | 1 | 0.77 |
| Способ размножения (С) | 0.77 | 0.77 | 0.9 | 0.77 | 1 |
Самой непохожей является пара признаков: «Вкус-Размер», у которых степень различия составляет 0.33, что составляет угол около 70 град. (близкий к 90 град.) между осями.
Можно сказать, что оси «Вкус-Размер» почти независимы. Точнее степень их зависимости (взаимозаменяемости) составляет всего 0.33.
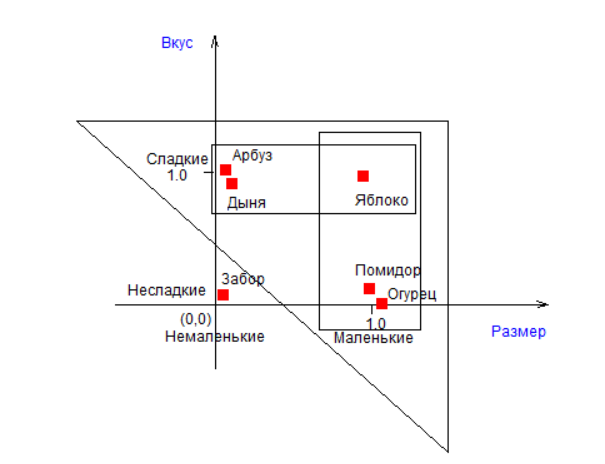
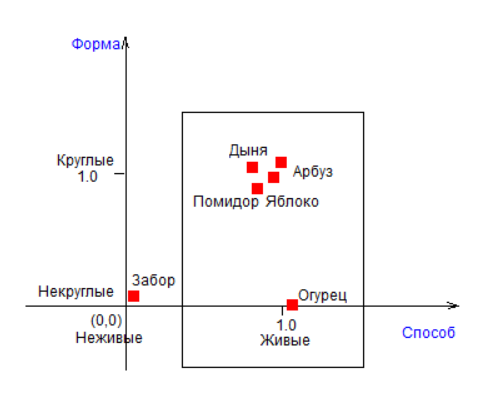
Итак, во-первых, результаты нашего анализа позволяют утверждать, что Вкус менее всего связан с Размером. Во-вторых, исходные данные, приведенные в таблице, показывают: объекты бывают сладкие маленькие, сладкие немаленькие, маленькие несладкие и немаленькие несладкие. То есть связи между Вкусом и Размером действительно нет. А, значит, предполагается, что эти оси хорошо дифференцируют (разделяют) Объекты в пространстве Признаков. Посмотрите на рисунок – все объекты почти равномерно распределились по пространству признаков «Вкус-Размер».
|
|
| Рисунок – Объекты и классы в проекции осей «Вкус-Размер» (видны классы «Фрукты», «Маленькие», «Фрукты-Овощи», «Живые», но оси не отличают Помидор от Огурца и Арбуз от Дыни) |
Кстати, информативность двух осей можно опять подсчитать по формуле Шеннона:
|
iвр = - 1/n1*lg2(1/n1) - 1/n2*lg2(1/n2) - 1/n3*lg2(1/n3) - 1/n4*lg2(1/n4) = - 2/6*lg2(2/6) - 1/6*lg2(1/6) - 2/6*lg2(2/6) - 1/6*lg2(1/6) = 1.92 бит
С другой стороны, наибольшая связь в данном примере наблюдается между координатами «Способ-Форма» (0,9). Действительно, исходные данные показывают, что если есть семечки, то объект круглый, исключение составляет только один объект «Огурец». Эти координаты практически взаимозаменяемы. Оси «Способ-Форма» в 3 раза хуже дифференцируют объекты, чем оси «Вкус-Размер». Объекты скучены в одной области и плохо различимы. Такие оси для задачи различения объектов почти бесполезны (информативность осей iфс ниже, чем в предыдущем случае iвр).
|
iфс = - 1/n1*lg2(1/n1) - 1/n2*lg2(1/n2) - 1/n3*lg2(1/n3) - 1/n4*lg2(1/n4) = - 1/6*lg2(1/6) - 1/6*lg2(1/6) - 4/6*lg2(4/6) - 0/6*lg2(0/6) = 1.25 бит
|
|
| Рисунок – Объекты и классы в проекции осей «Способ-Форма» (виден класс «Живые», оси плохо дифференцируют объекты по пространству) |
Итак, логично прежде всего принять за основу оси «Вкус-Размер». Но поскольку эти оси не полностью разделяют все объекты (путаются Арбуз с Дыней и Помидор с Огурцом), то в качестве дополнительных к основным осям ВР можно было бы добавить еще одну ось из оставшихся {Ц,Ф,С}. То есть следующую ось можно выбрать вычислением, присоединяя по очереди Ц, или Ф, или С к ВР, дополняя ВР до тройки осей.
Лучше всего, чтобы сумма углов между всеми тремя осями была максимальной. Или, что тоже, сумма абсолютных значений косинусов углов между всеми осями S была минимальной.
Оценим каждую из троек S.
Для тройки осей (В, Р, Ц) имеем S(В, Р, Ц) = |cos(Вкус, Размер)| + |cos(Вкус, Цвет)| + |cos(Размер, Цвет)| = 0,33 + 0,58 + 0,58 = 1,49.
Для тройки осей (В, Р, С) имеем S(В, Р, С) = |cos(Вкус, Размер)| + |cos(Вкус, Способ)| + |cos(Размер, Способ)| = 0,33 + 0,77 + 0,77 = 1,87.
Для тройки осей (В, Р, Ф) имеем S(В, Р, Ф) = |cos(Вкус, Размер)| + |cos(Вкус, Форма)| + |cos(Размер, Форма)| = 0,33 + 0,87 + 0,58 = 1,78.
Наилучшей тройкой осей и, таким образом, самыми независимыми признаками являются – Вкус, Размер и Цвет, у которой значение S самое маленькое.
То есть к осям «Вкус-Размер» имеет смысл добавить ось «Цвет».
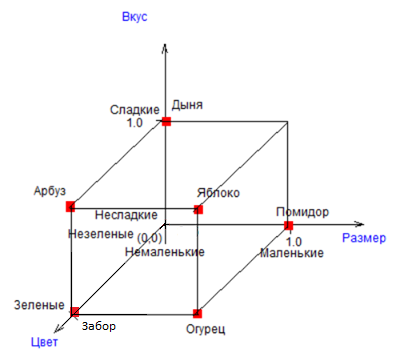
У нас получилось трехмерное пространство: «Вкус-Размер-Цвет», которое изображено на рисунке.
|
|
| Рисунок – Объекты и классы в осях «Вкус-Размер-Цвет» (все объекты разнесены по пространству по одному, достигнута максимальная дифференциация) |
Очевидно, что осей «Вкус-Размер-Цвет» достаточно для полной дифференциации всех классов. Информативность трех датчиков-осей составляет:
|
iврц = - 6*(1/n1*lg2(1/n1)) - 2*(1/n2*lg2(1/n2)) = - 6*1/6*lg2(1/6) - 2*0/6*lg2(0/6) = 2.59 бит. (Сама высокая информативность среди троек осей).
Такая же информативность у тройки ЦФР (2.59 бит). В этом смысле оси В и Ф взаимозаменяемы.
А к примеру тройка ВФС имеет информативность 1.79 бит и является самой неудачной, так как датчики имеют большую зависимость друг от друга. Исследование четверок, пятерок и т.д. в этом примере информативность не повышают, то есть трех датчиков вполне достаточно для поставленной задачи.
Исследуя информативность пар, троек и т.д. признаков, можно определить наилучшую комбинацию осей для представления робота о мире.
Остальные признаки избыточны. А тот, кто создавал исходную таблицу, проделал лишнюю работу, измеряя избыточные признаки и занося их в таблицу.
Если Вы возьмете другую тройку осей, то часть объектов останется неразличима по выбранным признакам.
Таким образом, мы определили размерность пространства существования наших объектов. Выбранные датчики «Вкус», «Размер», «Цвет», если их установить на робота, будут вполне справляться с задачей сортировки объектов. Заодно, заметим, что робот получил исчерпывающую информацию в мире заданных предметов и точно может дать определение каждому. Робот выделил и усвоил понятия мира заданных предметов.
Теоретическое обобщение
Как говорилось в самом начале, в одной стороны надо различать нюансы, а с другой – уметь обобщать, видеть общее в разном. Интересует сходство объектов (строк БД) и различие признаков (столбцов БД).
А для этого, во-первых, важно вообще исследовать пространство. Традиционно, размерность пространства задают. Однако, правильнее было бы выяснить его действительную размерность, которая задана мерами между точками в нем. Во-вторых, понять, линейно ли устроено это пространство или оно нелинейно, и можно ли его превратить в удобное линейное.
С точки зрения робота (искусственного интеллекта) было бы лучше, чтобы объекты были сгруппированы по классам, здесь важно, чтобы расстояние между объектами было поменьше, а между классами - побольше. В этом случае понимание мира у робота становится четче. А с точки зрения осей координат лучше, чтобы координаты были независимы, оси перпендикулярны, признаки уникальны. Тогда ясно, сколько и какие датчики должны быть у робота, чтобы он отчетливее воспринимал мир.
Здесь мы имеем право впервые использовать слово «понимание».
«Понять», это значит четко отличать один объект от другого, формулируя «сходство и отличие». Четко – это мера расстояния в пространстве признаков. «Понять» - это способность дать определение объекта через его признаки. Напомним, что «знать» - это способность установить связь между объектами, свойствами, поведениями в виде закона (причинно-следственной связи). Можно сказать так: «Понимают понятия, знают законы, умеют решать задачи, то есть преобразовывать законы».
Выделение признаков (атрибутов базы данных) – это вопрос наличия датчиков, внешнего интерфейса, того, как робот видит (ощущает) мир. Их набор должен быть максимально перпендикулярен друг другу, независим, образовывать базис. Датчиков должно быть максимально много (чтобы видеть мир во всем его многообразии), но все они должны быть перпендикулярны, в этом смысле – их набор должен быть минимален (без излишеств). Разрядность и границы восприятия датчиков должны быть достаточными с точки зрения точности различения объектов.
«Необходимая и достаточная возможность в ощущениях».
Примечание. Слегка упреждая дальнейшее повествование, скажем, что мышление человечества существует в 75-мерном пространстве, 4 оси в котором - основные, то есть составляют базис мышления (это минимальное количество независимых осей координат).
Ощущения (свойства): вкус (4+1 вкуса), запах (зависимая переменная), цвет (750 000 цветов по амплитуде и 7 000 000 рецепторов по пространству), свет (100 000 000 по пространству, разрешение по амплитуде - 1010, разрешение по времени - 25 Гц – 3 оси), механическое давление, температура, электрическое и химическое воздействие.
Элементарные законы - мозг содержит 1011 нейронов, 1015 связей нейронов. 1 нейрон – 1 линейная функция. 1 связь – 1 ось координат.
Классы (кластеры записей базы данных) – вопрос создания модели мира внутри робота, того, как робот представляет себе (понимает) мир, их набор должен быть разнороден в классах (максимальная энтропия, классы должны сильно различаться) и однороден внутри классов (минимальная энтропия, объекты класса должны минимально различаться). То есть количество уравнений (классов) должно быть оптимально. Наш мозг ищет сгустки энтропий распределения понятий и законов в пространстве ощущений-признаков.
Переменные – это ощущения. Уравнения, причинно-следственные связи – это знания.
Примечание. Обратите внимание, что в нашем примере оси «Вкус-Размер-Цвет» не вполне ортогональны, значение S для них не равно минимальному значению, нулю. А это говорит о том, что по значениям одного признака можно с определенной точностью предсказывать значение другого признака – признаки зависимы.
Правильно было бы начертить на рисунке эти оси по отношению друг к другу под выше вычисленными нами углами: cos(71 град.) = 0,33, cos(55 град.) = 0,57.
Используя значения углов, можно также сказать, что Вкус = 0.33*Размер, Вкус = 0.58*Цвет, Размер = 0.58*Цвет. То есть мы можем указать, насколько Вкус связан с Цветом, или, другими словами, насколько Вкус определяет Цвет.
Теперь, зная, какой признак сколько вносит от себя определенности в название объекта, можем составить уравнение класса.
Уравнения модели
На основе полученных нами координат построим модель, то есть с помощью системы уравнений опишем сразу все наши данные, представленные в таблице. Система уравнений (модель) своей компактной записью заменяет множество табличных данных. Таблицу любого размера можно заменить на одно или несколько компактных уравнений. Это очень удобно.
Три уравнения имеют вид тождества:
Вкус = Вкус, Размер = Размер, Цвет = Цвет.
Например, уравнение, вычисляющее «Сладкий/Несладкий» вкус у объекта, говорит нам о том, что если Вкус=0, то объект несладкий, если Вкус = 1, то объект сладкий. Объект считается сладким, если переменная Вкус принимает положительное значение, и наоборот, объект считается несладким, если переменная Вкус принимает неположительное значение (0 или <0).
Уравнение, вычисляющее способ размножения объекта «Семечки/Без семечек», имеет вид:
Способ размножения = 2*Вкус + 2*Размер - 2*Цвет + 1.
Уравнение, вычисляющее форму объекта «Круглый/Некруглый», имеет вид:
Форма = 2*Вкус - 2*Цвет + 1.
В общем виде любое из уравнений имеет вид:
Признак = Функция (В, Р. Ц).
(Вывод уравнений производится в отдельном разделе курса «Регрессионные модели»).
Следствие 1
Уравнения говорят нам о том, что если вы знаете вкус, размер и цвет объекта, то в принципе можете определить – размножается семечками он или нет, круглый или нет.
В таблице приведены значения всех пяти функций для всех значений объектов:
| Вкус | Размер | Цвет | Способ размножения: С = 2*В + 2*Р - 2*Ц + 1 | Форма: Ф = 2*В - 2*Ц + 1 | |
| Арбуз | 1 | 0 | 1 | 1 | 1 |
| Яблоко | 1 | 1 | 1 | 3 | 1 |
| Дыня | 1 | 0 | 0 | 3 | 3 |
| Помидор | 0 | 1 | 0 | 3 | 1 |
| Огурец | 0 | 1 | 1 | 1 | -1 (не круглый) |
| Забор | 0 | 0 | 1 | -1 (не семечками) | -1 (не круглый) |
Зная уравнения классов, можно определить для объекта, заданного значащими признаками {В, Р, Ц}, недостающие признаки {Ф, С}, поскольку они зависимы от {В, Р, Ц}.
Следствие 2
Отличие модели от данных (уравнения от таблицы) заключается в том, что, имея уравнение, Вы можете получать новые, ранее неизвестные Вам данные. Это происходит потому, что модель отражает общую закономерность, имеющуюся в исходных данных. Имея просто таблицу данных, Вы, к сожалению, не можете получать из нее новые данные, если их нет в таблице.
Данные не порождают новые данные.
Новые факты порождает только закономерность, модель. Этот процесс называется прогнозированием. Прогноз – неотъемлемое и важнейшее свойство модели. Если некоторая информация не позволяет предсказывать новые данные, то она является данными, если позволяет - моделью.
Информация, согласно теореме Геделя, имеет разные формы: данные, модели, алгебры, группы алгебр, … .
Продемонстрируем, что наша модель обладает свойством прогнозирования.
Предскажем, какими свойствами обладают новые объекты «Киви» и «Здание», информации о которых не было в таблице данных. На кого похожи новые объекты, к каким классам их можно отнести?
Исходно киви имеет признаки: В = 1 (сладкий), Р = 1 (маленький), Ц = 1 (зеленый). Уточняя по уравнениям (подставляя значения В, Р, Ц в уравнения), определяем, что объект «Киви» – сладкий, зеленый, маленький, живой, размножается семечками (С = 3), круглый (Ф = 1). Что соответствует истине, прогноз оказался правильным.
Ближе всего киви к яблоку (сумма отличий равна 2), арбузу (сумма отличий - 3), дыне (сумма отличий - 4).
Отличие, например, мы подсчитали так: |Вкиви - Вяблока| + |Ркиви - Ряблока| + |Цкиви - Цяблока| + |Скиви - Сяблока| + |Фкиви - Фяблока| = |1-1|+|1-1|+|1-1|+|3-1|+|1-1| = 2.
Здание имеет признаки: В = 0 (не сладкое), Р = 0 (не маленькое), Ц = 0 (не зеленое).
Объект «Здание» – не сладкий, не зеленый, не маленький, живой (С = 1 ), круглый (Ф = 1 ). Ближе всего здание к забору (три отличия) и помидору (одно отличие). Прогноз, конечно, не удовлетворительный, так как здание путается с помидором и определяется как «живой».
Примечание. Обратите внимание, прогнозируя, мы можем получить в ряде случаев определенную неточность или даже ошибку. Как это видно в примере со зданием. Это связано с тем, что для анализа и построения модели использовалось слишком мало данных. Чем больше данных нам предоставляется, тем точнее будет модель, которую мы строим.
Если в таблице появятся здания разного цвета, разной формы, разного размера, но без вкуса и без семечек, то система перестроит оси и уравнения и будет прогнозировать более точно.
С = 0,75*В + 0,75*Р - 0,25
Ф = В + 0,5*Р - 0,25*Ц - 0,25
Теперь проверка «киви» дает: С = 1,25 (размножается семечками), Ф = 1 (круглый), прогноз верный.
Проверка «здание» дает: С = -0,25 (объект не размножается семечками), Ф = -0,25 (объект не круглый), прогноз верный.
Новые уравнения предсказывают результат более точно, то есть являются более адекватными, больше соответствуют действительности.
Интеллект. Обучение, прогнозирование, управление
Система уравнений представляет каждый рассматриваемый объект во всех его свойствах и может полностью заменить таблицу данных. Такая система уравнений может прогнозировать свойства новых объектов и принадлежность их к установленным нами классам, а, значит, является моделью. В отличие от таблицы, которая может только показывать нам старые объекты и ничего не говорит о новых.
Отличие модели от данных состоит в том, что модель обладает способностью прогнозировать, выводить новые данные.
Такова уникальная способность интеллектуальных систем. Система называется интеллектуальной, если она способна прогнозировать будущее, определять неизвестное на основании известных частных фактов, обобщать. Зная следствия, мы можем избегать будущие неприятные ситуаций, моделируя их заранее в своем воображении, то есть до того, как они наступили.
Основная особенность интеллекта – способность анализировать известные данные, на их основе строить модели и использовать эти модели для прогноза будущих ситуаций, новых данных. Зная возможные будущие ситуации, будущее поведение, новые данные, можно предвидеть неприятные ситуации, избегать их, стремиться к наиболее благоприятным из них, извлекать из бесконечной материи, энергии, информации природы пользу, повышать кпд своих действий - меньше затрачивать, получая больше результатов.
Процесс получения модели из данных называется обучением.
Процесс получения новых данных по построенной модели называется прогнозированием.
Процесс установления на модели условий, которые ведут к благоприятным будущим результатам, называется управлением.
То, что в состоянии строить модели, используя доступные данные, и с их помощью решать задачи, искать нужные решения, избегать неприятностей в практической деятельности, оптимизировать свое поведение, может претендовать на звание интеллектуальной системы.
Разумеется, любая модель является приближенной, поскольку мир, который нас окружает, бесконечен. Для построения все более точных моделей необходимо учитывать все большее количество фактов, данных. Собственно, именно так, например, делает Google.
Система Google с помощью таких механизмов сбора данных, как Facebook, Twitter, перехватывая и обрабатывая e-mail, sms, непрерывно строит и корректирует модели своих пользователей, благодаря большим массивам собираемых данных. Знание о пользователях, их предпочтениях и свойствах позволяет прогнозировать их поведение, реакции на те или иные события. Эта информация интересна для прогнозирования продаж товаров, эффекта рекламы, раннего обнаружения опасных социальных событий.
Поведение интеллектуальной системы стремится к адекватному за счет приближения модели, формируемой в «голове» такой системы, к максимально соответствующей окружающему миру.
Поскольку окружающий нас мир непрерывно меняется, чтобы выжить, необходимо непрерывно уточнять свое представление о мире, изменять свою модель мира. Только так наша деятельность будет приносить плоды и позволит избежать неприятностей.
Примечание. Важно, какие именно признаки для характеристики объектов мы выбираем. Если выбрать не очень удачные признаки (например, шершавость или электропроводность для фруктов), то и результат расчетов будет неудачный. В общем случае, когда не понятно, какие признаки следует брать, поступать надо так: «чем больше признаков вы возьмете, тем лучше». Неинформативные признаки отпадут потом сами собой в процессе расчетов.
Примечание. Если в таблице заранее не содержится никакой закономерной информации, то подобное исследование, разумеется, не обнаружит никакой закономерности (если данных много) или обнаружит ложную закономерность (если данных мало). Модель в этом случае будет очень большой, рыхлой.
При объединении нескольких объектов в один класс возникает проблема описания нового объекта, обобщения описания нового класса, получение формулы класса. Это необходимо для вывода уравнений класса как функции объединенных признаков.
Ранее мы определили последовательность формирования все более общих классов в нашем примере так: А - Я(0,9) - Д(0,39) - П(0,14) - О(0.04) - З(0). В скобках указан уровень похожести, при котором объекты начинают объединяться в классы.
Вектор (1 1 1 1 1) включает все признаки Ц, В, Ф, Р, С.
Пересекая Арбуз (1 1 1 0 1) с (1 1 1 1 1), получаем (1 1 1 0 1).
Далее пересекаем получившийся Класс (1 1 1 0 1) с Яблоком (1 1 1 1 1), получаем (1 1 1 0 1).
Далее, присоединяя объект Дыня (0 1 1 0 1) к получившемуся классу, снова после пересечения получаем (0 1 1 0 1).
Обратим внимание, что класс, объединяющий АЯД, имеет вид (0 1 1 0 1). Он объединяет все эти объекты (А, Я, Д) в один новый класс «сладкий» вкус, «круглая» форма и «семечки».
При необходимости такие промежуточные классы могут иметь свои индивидуальные названия, например, «Фрукты».
Далее, присоединяя объект Помидор (0 0 1 1 1) к получившемуся классу, получаем после пересечения новый общий класс (0 0 1 0 1). То есть класс АЯДП имеет вид (0 0 1 0 1). Объединяет все эти объекты в один класс «круглая» форма и «семечки».
Присоединяя Огурец (1 0 0 1 1) к этому классу, имеем АЯДПО (0 0 0 0 1). Объединяет все эти объекты в один класс наличие свойства «семечки». Имеет смысл назвать этот класс «Фрукты-Овощи». Запасные названия для киоска «Овощи-Фрукты»: «С семечкой», «Растения», «Выросло из семечки».
Присоединяя Забор (0 0 0 0 0) к этому классу, имеем (0 0 0 0 0).
Хорошее название этого магазина – «1000 мелочей», «У нас есть все» или «Белый шум» :)
Обсудим важность (общность тех или иных признаков), фундаментальность осей координат по отношению друг к другу. Одни признаки являются решающими для отнесения объекта к классу, другие мало на что влияют.
Обратите внимание на порядок присоединения признаков <Ц, В, Ф, Р, С> по мере укрупнения классов <А, Я, Д, П, О, З>:
| (Цвет | Вкус | Форма | Размер | Способ) | |
| АЯДПОЗ | (0 | 0 | 0 | 0 | 0) |
| АЯДПО | (0 | 0 | 0 | 0 | 1) |
| АЯДП | (0 | 0 | 1 | 0 | 1) |
| АЯД | (0 | 1 | 1 | 0 | 1) |
| АЯ | (0 | 1 | 1 | 0 | 1) |
| А | (1 | 1 | 1 | 0 | 1) |
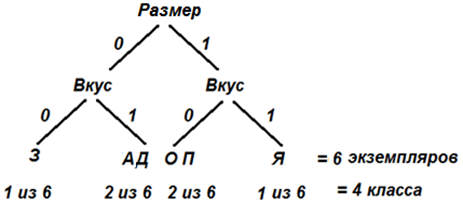
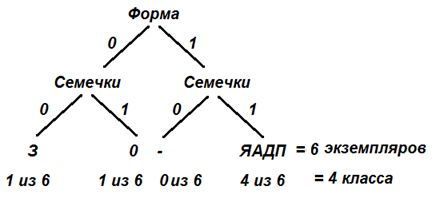
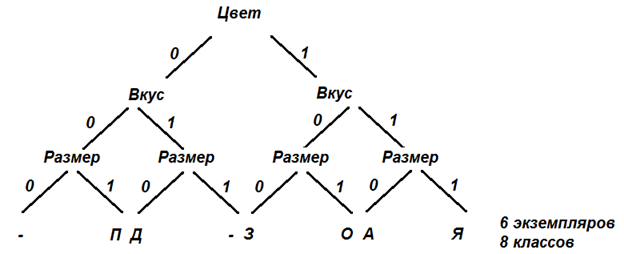
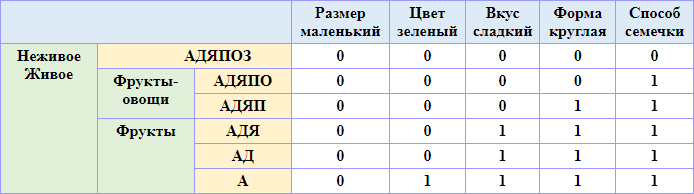
Или упорядочивая признаки по мере их появления в формуле классов (путем перестановки столбцов):
|
Примечание. В таблицу введены промежуточные названия классов, которые люди часто используют в своей практической деятельности (фрукты, фрукты-овощи, живое, неживое). Геометрия помогла нам получить иерархию классов и подробно распределить по ним множество исходных объектов.
Из таблицы видно, что самый маловажный признак, используемый в характеристике объектов, - размер, так как он практически никак не учитывается в отнесении объекта к какому-либо классу. За ним в порядке возрастания важности идут «зеленый» цвет, «сладкий» вкус, «круглая» форма, «семечки».
Способ размножения «семечки» – самый важный признак. Видно, что признаком «живого» является свойство «семечки».
Из таблицы видно, что признаком класса «Фрукт» является «сладкий» вкус.
Внимание! Может показаться, что признаком для «Овощей» является «несладкий» вкус, но это не так, так как этим свойством обладает также и Забор. Поэтому для выделения формулы овощей следует применять более сложное логическое выражение. Например, так: Овощ = «несладкий» вкус И «семечки». Подобные выражения, используя таблицу, можно вывести для каждого класса иерархии.
Заметим, что порядок важности осей координат совпал с ранее выделенным списком:
| Цвет | 2.43 |
| Вкус | 2.65 |
| Форма | 2.85 |
| Размер | 2.26 |
| Способ | 3.21 |
Теперь можно составить определения понятий и множества примеров.
1. Фрукт – это (Вкус = Сладкие).
Читать эту запись следует так: «Фрукт – это объект, обладающий сладким вкусом».
Под это определение из таблицы попадают (то есть к фруктам относятся) {Арбуз, Яблоко, Дыня}.
2. Овощи – это (Вкус=НЕ Сладкие) И (Способ=Живые). То есть «Овощ – это объект с несладким вкусом и размножающийся семечками (то есть живой)». Под это определение из таблицы попадают (то есть к овощам относятся) {Огурец, Помидор}. И так далее.
Заключение с обобщением (не для всех)
Формулу вычисления сходства для двух объектов со множеством признаков можно обобщить. Косинус – это скалярное произведение векторов свойств объектов, деленное на модули объектов. В выражении числителя косинуса присутствует сумма произведений, то есть сумма с очень большим количеством слагаемых, от переменной, выполняющей роль перечисления признаков.
Итак, сходство двух объектов f и g с признаками х: f(x) и g(x), где f и g – два объекта, а х – набор признаков, вычисляется так:
сходство = ∫(f(x)*g(x)*dx/√(∫f 2(x)*dx*∫g 2(x)*dx),
а интеграл (сумма) берется по всем признакам (-∞; +∞). Нетрудно видеть, что это выражение есть формула корреляции функций f(x) и g(x).
Если в качестве функции g(x) взять ортогональные функции, например, cos(w*x) или (и) sin(w*x) – гармоники, то получим ряд чисел (коэффициентов ряда Фурье), указывающих на разложение f(x) в этот базис. Что позволяет построить любую сложную систему из ограниченного набора простых элементов (базиса), достаточно только взять в сумму каждое простое слагаемое из базиса с соответствующим весом (коэффициентом его похожести на f(x)).
Разумеется, конструкторы (наборы простых элементов) могут быть разными. Важно, чтобы все элементы в них были взаимно перпендикулярны друг другу, максимально непохожи. Перпендикулярность элементов позволяет складывать сложные конструкции линейно.
На этом основаны базис Хоара, Уолша, Ньютона, Фурье, Штурма, Крижевского, Ле Куна (нейроны, глубокое обучение, распознавание образов).
А сам искусственный интеллект представляет собой – систему уравнений, которые задают гиперплоскости в многомерном пространстве признаков, которые делят это пространство на области (классы, кластеры), в которых компактно собираются схожие объекты. Описанием объекта является название класса. Определением класса является вектор проекций границ класса на систему координат многомерного пространства. Признаки являются датчиками робота, ощущениями человека, а классы – сложными понятиями, уравнения классов (причинно-следственные отношения) – пониманием устройства мира. Корни системы уравнений – условия равновесия - задают свойства новой системы, образованной понятиями и связями (уравнениями) и соответствуют знанию мира. Свойства – интервалы между двумя соседними корнями, или области, образованные проекциями системы уравнений на плоскости, натянутые на оси координат.
Задание
1. Задаться примером для метода k-means (не менее 3D, не менее 15 экземпляров). Провести кластеризацию множества экземпляров для случаев: k = 2, k = 3, k = 4. Нарисовать дерево классов. Привести графическую иллюстрацию.
2. Задаться примером. Методом «Косинуса» провести анализ классов, вывести дерево классов, правила, провести прогноз на модели, нарисовать геометрическую иллюстрацию, выбрать датчики, привести регрессионную модель.
Например, найдите классы автомобилей.
|
| О руководителе курса «Моделирование систем» | Лекция 02. Линейные регрессионные модели | ||||||||||||||||
|
|||||||||||||||||