|
Практическое занятие 2.
|
|
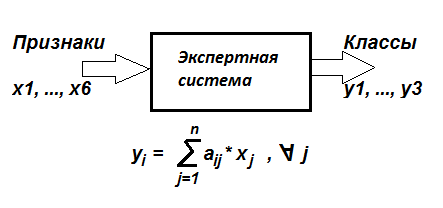
Y1 = a11*x1 + a12*x2 + a13*x3 + a14*x4 + a15*x5 + a16*x6
Y2 = a21*x1 + a22*x2 + a23*x3 + a24*x4 + a25*x5 + a26*x6
Y3 = a31*x1 + a32*x2 + a33*x3 + a34*x4 + a35*x5 + a36*x6
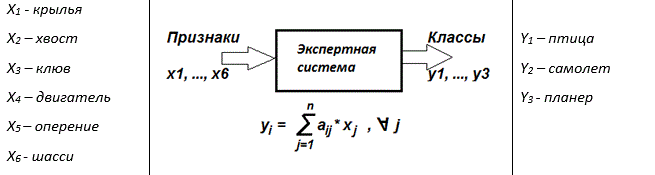
Задача системы состоит в том, чтобы самостоятельно найти значения коэффициентов aij модели в линейной форме. Как только коэффициенты будут найдены, а уравнения составлены (система перестанет ошибаться), систему можно будет использовать для предсказания. Значения коэффициентов уравнений находят в процессе настройки модели по известным величинам входа xi и выхода уj. Для этого системе предъявляют примеры, на которых она учится.
То есть размер матрицы коэффициентов линейной системы уравнений aij - 6 на 3. Столбцы – классы: y1,y2,y3. Строки – признаки x1,x2,x3,x4,x5,x6. Начальное состояние матрицы нулевое:
| Y1 | Y2 | Y3 | |
| x1 | 0 | 0 | 0 |
| x2 | 0 | 0 | 0 |
| x3 | 0 | 0 | 0 |
| x4 | 0 | 0 | 0 |
| x5 | 0 | 0 | 0 |
| x6 | 0 | 0 | 0 |
Итерация 1.
Переведем систему в режим обучения.
Предъявляем системе пример 1: класс Y1 обладает следующими признаками x1=1, x2=1, x3=1, x4=0, x5=1, x6=0. То есть класс А – это «птица», y1=1. Птица обладает крыльями (x1=1), обладает хвостом (x2=1), обладает клювом (x3=1), не имеет двигателя (x4=0), обладает оперением (x5=1), не имеет шасси (x6=0).
Вектор Х=(111010) прибавляется (поощрение!) к столбцу Y1 и вычитается (наказание!) из столбцов Y2 и Y3.
![]() Применен принцип обучения «наказывай за неверное и поощряй за правильное», так называемый принцип «кнута и пряника».
Применен принцип обучения «наказывай за неверное и поощряй за правильное», так называемый принцип «кнута и пряника».
Например, к первому столбцу (0,0,0,0,0,0) прибавляем вектор (1,1,1,0,1,0), получаем новое значение столбца (1,1,1,0,1,0).
Второй столбец наказываем, так как птица не есть самолет: из столбца (0,0,0,0,0,0) вычитаем вектор (1,1,1,0,1,0). Получаем новое значение второго столбца – (-1,-1,-1,0,-1,0). И так далее…
Получаем в итоге следующий вид матрицы после обучения примеру 1: (1,1,1,0,1,0) – это «птица».
| 1 | -1 | -1 |
| 1 | -1 | -1 |
| 1 | -1 | -1 |
| 0 | 0 | 0 |
| 1 | -1 | -1 |
| 0 | 0 | 0 |
Для проверки переведем систему в режим экспертизы. Предъявим ей в качестве примера птицу (111010). Для экспертизы умножим вектор (111010) на только что полученную матрицу.
|
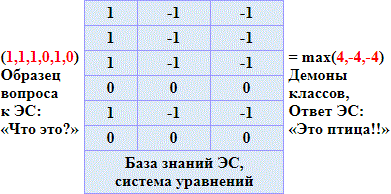
Результат в первом столбце равен 1*1 + 1*1 + 1*1 + 0*0 + 1*1 + 0*0 = 4.
Результат во втором столбце равен 1*(-1) + 1*(-1) + 1*(-1) + 0*0 + 1*(-1) + 0*0 = -4.
Результат в третьем столбце равен 1*(-1) + 1*(-1) + 1*(-1) + 0*0 + 1*(-1) + 0*0 = -4.
Вектор (4, -4, -4) называется вектором демонов. Демоны показывают, насколько они уверены в опознании того или иного класса. Значение величины «голос демона» – уверенность, степень похожести предъявленного объекта на один из классов.
Из вектора (4, -4, -4) следует выбрать класс, характеризуемый максимальным числом (используем принцип демона: «кто громче крикнет, тот и прав»). Это класс Y1, число 4. То есть предъявленный объект опознан как птица. ИС опознала объект правильно.
Если в качестве примера предъявить объект, которому система не была обучена, например, самолет, то результат будет не верным или не точным. Причина в том, что информацию о самолетах или планерах система еще не получала. В коэффициентах такой информации еще не заложено.
Проверьте этот факт экспериментально на модели.
Итерация 2.
Переведем систему в режим обучения.
Предъявляем системе пример 2: класс Y2 - самолет обладает крыльями (x1 = 1), обладает хвостом (x2 = 1), не имеет клюва (x3 = 0), имеет двигатель (x4 = 1), не имеет оперения (x5 = 0), имеет шасси (x6 = 1).
Вектор (110101) прибавляется (поощрение!) к столбцу Б предыдущей матрицы и вычитается (наказание!) из столбцов А и В. Получаем следующий вид матрицы после обучения примеру 2.
| 0 | 0 | -2 |
| 0 | 0 | -2 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
Для проверки эффективности обучения переведем систему в режим экспертизы. Предъявим ей в качестве примера птицу (111010). Для экспертизы умножим вектор (111010) на матрицу.
Результат в первом столбце равен 1*0 + 1*0 + 1*1 + 0*(-1) + 1*1 + 0*(-1) = 2.
Результат во втором столбце равен 1*0 + 1*0 + 1*(-1) + 0*1 + 1*(-1) + 0*1 = -2.
Результат в третьем столбце равен 1*(-2) + 1*(-2) + 1*(-1) + 0*(-1) + 1*(-1) + 0*(-1) = -6.
Из вектора (2, -2, -6) следует выбрать класс, характеризуемый максимальным числом. Это класс А, число 2. То есть предъявленный объект опознан как птица.
Предъявим ей в качестве примера самолет (110101). Для экспертизы умножим вектор (110101) на матрицу.
Результат в первом столбце равен 1*0 + 1*0 + 0*1 + 1*(-1) + 0*1 + 1*(-1) = -2.
Результат во втором столбце равен 1*0 + 1*0 + 0*(-1) + 1*1 + 0*(-1) + 1*1 = 2.
Результат в третьем столбце равен 1*(-2) + 1*(-2) + 0*(-1) + 1*(-1) + 0*(-1) + 1*(-1) = -6.
Из вектора (-2, 2, -6) следует выбрать класс, характеризуемый максимальным числом. Это класс Б, число 2. То есть предъявленный объект опознан как самолет.
Вывод. Система научилась распознавать классы Y1 и Y2, на которых была обучена.
Итерация 3.
Переведем систему в режим обучения.
Предъявляем системе пример 3: класс Y3 – планер обладает крыльями (x1 = 1), обладает хвостом (x2 = 1), не имеет клюва (x3 = 0), не имеет двигателя (x4 = 0), не имеет оперения (x5 = 0), не имеет шасси (x6 = 0).
Вектор (110000) прибавляется (поощрение!) к столбцу В предыдущей матрицы и вычитается (наказание!) из столбцов Y1 и Y2. Получаем следующий вид матрицы после обучения примеру 3.
| -1 | -1 | -1 |
| -1 | -1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
Для проверки эффективности обучения переведем систему в режим экспертизы. Предъявим ей в качестве примера птицу (111010). Для экспертизы умножим вектор (111010) на матрицу.
Результат в первом столбце равен 1*(-1) + 1*(-1) + 1*1 + 0*(-1) + 1*1 + 0*(-1) = 0.
Результат во втором столбце равен 1*(-1) + 1*(-1) + 1*(-1) + 0*1 + 1*(-1) + 0*1 = -4.
Результат в третьем столбце равен 1*(-1) + 1*(-1) + 1*(-1) + 0*(-1) + 1*(-1) + 0*(-1) = -4.
|
Из вектора (0, -4, -4) следует выбрать класс, характеризуемый максимальным числом. Это класс Y1, число 0. То есть предъявленный объект опознан как птица.
Предъявим ей в качестве примера самолет (110101). Для экспертизы умножим вектор (110101) на матрицу.
Результат в первом столбце равен 1*(-1) + 1*(-1) + 0*1 + 1*(-1) + 0*1 + 1*(-1) = -4.
Результат во втором столбце равен 1*(-1) + 1*(-1) + 0*(-1) + 1*1 + 0*(-1) + 1*1 = 0.
Результат в третьем столбце равен 1*(-1) + 1*(-1) + 0*(-1) + 1*(-1) + 0*(-1) + 1*(-1) = -4.
|
Из вектора (-4, 0, -4) следует выбрать класс, характеризуемый максимальным числом. Это класс Y2, число 0. То есть предъявленный объект опознан как самолет.
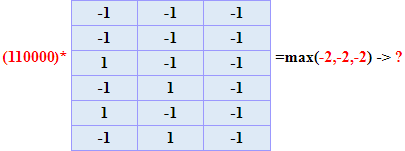
Предъявим ей в качестве примера планер (110000). Для экспертизы умножим вектор (110000) на матрицу.
Результат в первом столбце равен 1*(-1) + 1*(-1) + 0*1 + 0*(-1) + 0*1 + 0*(-1) = -2.
Результат во втором столбце равен 1*(-1) + 1*(-1) + 0*(-1) + 0*1 + 0*(-1) + 0*1 = -2.
Результат в третьем столбце равен 1*(-1) + 1*(-1) + 0*(-1) + 0*(-1) + 0*(-1) + 0*(-1) = -2.
|
Из вектора (-2, -2, -2) невозможно выбрать класс, характеризуемый максимальным числом. Предъявленный объект неопознан. Следует продолжать обучение.
Итерация 4.
Переведем систему в режим обучения. Последний раз матрица ЭС имела вид:
| -1 | -1 | -1 |
| -1 | -1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
![]() Повторим пример. Используется принцип «повторение – мать учения».
Повторим пример. Используется принцип «повторение – мать учения».
Предъявляем системе пример 3: класс Y3 – планер обладает крыльями (x1 = 1), обладает хвостом (x2 = 1), не имеет клюва (x3 = 0), не имеет двигателя (x4 = 0), не имеет оперения (x5 = 0), не имеет шасси (x6 = 0).
Вектор (110000) прибавляется (поощрение!) к столбцу Y3 предыдущей матрицы и вычитается (наказание!) из столбцов Y1 и Y2. Получаем следующий вид матрицы после обучения примеру 3.
| -2 | -2 | 0 |
| -2 | -2 | 0 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
Внимание! Чтобы система не выходила за гиперкуб, то есть, чтобы в матрице не накапливались числа по модулю больше 1, скорректируем матрицу, вернув ее на ближайшую границу (1 или -1). Кстати, это можно было сделать на предыдущей операции (итерация #2), когда система вышла за гиперкуб. Однако, поскольку общей теории на этот счет нет (иногда выход за гиперкуб полезен для устойчивой работы системы, иногда - нет), то оставляют принятие решения о нормализации матрицы на усмотрение пользователя. (В программном продукте появляется кнопка «Нормализовать», которую нажимает (или не нажимает) пользователь).
| -1 | -1 | 0 |
| -1 | -1 | 0 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
Для проверки эффективности обучения переведем систему в режим экспертизы. Предъявим ей в качестве примера птицу (111010). Для экспертизы умножим вектор (111010) на матрицу.
Результат в первом столбце равен 1*(-1) + 1*(-1) + 1*1 + 0*(-1) + 1*1 + 0*(-1) = 0.
Результат во втором столбце равен 1*(-1) + 1*(-1) + 1*(-1) + 0*1 + 1*(-1) + 0*1 = -4.
Результат в третьем столбце равен 1*0 + 1*0 + 1*(-1) + 0*(-1) + 1*(-1) + 0*(-1) = -2.
Из вектора (0, -4, -2) следует выбрать класс, характеризуемый максимальным числом. Это класс Y1, число 0. То есть предъявленный объект опознан как птица.
Предъявим ей в качестве примера самолет (110101). Для экспертизы умножим вектор (110101) на матрицу.
Результат в первом столбце равен 1*(-1) + 1*(-1) + 0*1 + 1*(-1) + 0*1 + 1*(-1) = -4.
Результат во втором столбце равен 1*(-1) + 1*(-1) + 0*(-1) + 1*1 + 0*(-1) + 1*1 = 0.
Результат в третьем столбце равен 1*0 + 1*0 + 0*(-1) + 1*(-1) + 0*(-1) + 1*(-1) = -2.
Из вектора (-4, 0, -2) следует выбрать класс, характеризуемый максимальным числом. Это класс Y2, число 0. То есть предъявленный объект опознан как самолет.
Предъявим ей в качестве примера планер (110000). Для экспертизы умножим вектор (110000) на матрицу.
Результат в первом столбце равен 1*(-1) + 1*(-1) + 0*1 + 0*(-1) + 0*1 + 0*(-1) = -2.
Результат во втором столбце равен 1*(-1) + 1*(-1) + 0*(-1) + 0*1 + 0*(-1) + 0*1 = -2.
Результат в третьем столбце равен 1*0 + 1*0 + 0*(-1) + 0*(-1) + 0*(-1) + 0*(-1) = 0.
Из вектора (-2, -2, 0) следует выбрать класс, характеризуемый максимальным числом. Это класс Y3, число 0. То есть предъявленный объект опознан как планер.
Выводы
После четырех итераций обучения система устойчиво опознает каждый из предъявляемых ей классов. Уверенность системы измеряется расстоянием между компонентами вектора {Y}.
Так как экспертиза птицы дает вектор демонов вида (0, -4, -2), то от планера, по мнению системы, птицу отделает расстояние 2, от самолета 4. То есть птица более похожа на планер, чем на самолет.
В свою очередь самолет более похож на планер, чем на птицу, так как имеет вектор (-4, 0, -2).
Вычислим разницу векторов (определений классов) по хэминговой мере:
Птица – Самолет = (1, 1, 1, 0, 1, 0) - (1, 1, 0, 1, 0, 1) = 4 (эти вектора отличаются друг от друга в четырех позициях, в каждой позиции отличие составит 1).
Для примера сделаем вычитание векторов столбиком.
| 1 | 1 | 1 | 0 | 1 | 0 | Вектор «птица» |
| 1 | 1 | 0 | 1 | 0 | 1 | Вектор «самолет» |
| 0 | 0 | 1 | |-1|=1 | 1 | |-1|=1 | Сумма различий = 4 |
Далее:
Птица – Планер = (1, 1, 1, 0, 1, 0) - (1, 1, 0, 0, 0, 0) = 2
Самолет – Планер = (1, 1, 0, 1, 0, 1) - (1, 1, 0, 0, 0, 0) = 2
Нарисуем объекты, как они располагаются в мире, и расстояния между ними.
|
|
| Рисунок – Расположение объектов в мире, как есть |
Мы использовали внешнюю информацию {Х} о положении изучаемых объектов в мире. То есть это описание «мира», каков мир есть. Мир представлен нам экспериментальными данными, примерами.
Заметим, что модель «мира» отличается от описания самого «мира» и находится в обученной матрице, в мозгах экспертной системы. Ищем различия между построенными системой классами, то есть вычитаем один столбец матрицы коэффициентов из другого. Тем самым мы подсчитываем разницу между классами «птица», «самолет», «планер» в сознании самой системы, которая как-то отражает сейчас наблюдаемый ею мир.
| -1 | -1 | 0 |
| -1 | -1 | 0 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
Вычисляем модель в мозге системы, определив различия между объектами в «сознании» системы, то есть в коэффициентах aij.
Птица – Самолет = (-1, -1, 1, -1, 1, -1) - (-1, -1, -1, 1, -1, 1) = 8
Птица – Планер = (-1, -1, 1, -1, 1, -1) - (0, 0, -1, -1, -1, -1) = |-6| = 6
Самолет – Планер = (-1, -1, -1, 1, -1, 1) - (0, 0, -1, -1, -1, -1) = |-6| = 6
|
|
| Рисунок – Расположение объектов в сознании интеллектуальной системы, как ИС представляет окружающий мир через обучение |
Обратите внимание! Рисунок «Объекты в «мире» и рисунок «Объекты в «сознании» системы» подобны, но не совпадают. Планер находится между самолетом и птицей.
Мир познан не абсолютно. Модель не является 100% отражением мира, однако является его подобием. Если продолжать обучать систему примерами, то модель «мира в сознании системы» будет приближаться к модели «мира».
«Повторение – мать учения» - принцип работы таких систем.
Обратите внимание, что система сама пришла к выводу, что ее мир объектов двухмерен. Размерность пространства мира продиктовано не директивностью учителя, а свойствами меры и объектов в нем.
Прогноз – важнейшее свойство ИС
Важнейшим свойством интеллектуальных систем является их способность работать с новыми объектами, которые им ранее при обучении не предъявлялись. Это говорит о том, что система есть не база данных, а модель, знание, зависимость, закон, уравнение. В уравнение вшита способность описывать множество значений переменных, удовлетворяющих ему. Модель обобщает данные, устанавливая причинно-следственную связь. Модель представляет собой уравнение (или систему уравнений), в котором выражения причин и следствия соединены знаком причинно-следственной связи: «=».
Построение модели, вывод знания из фактов, алгебраического уравнения из арифметических данных - цель и отличительная особенность ИС.
ИС второго уровня строят модели из данных, третьего – алгебры, обобщая модели, четвертого – алгебры алгебр (системы алгебр) и так далее.
Поэтому, построив модель, следует, проверяя ее работу в режиме экспертизы, испытать ее способность к предсказанию на новом неизвестном ей из примеров объекте.
После предъявления ранее незнакомого объекта система ищет наиболее похожий к нему из известных ей классов. Например, предъявим к экспертизе системой ракету (010100). Такого примера еще не было и система не знает, что такое ракета. Но увидев ракету, система может понять, на что ракета больше похожа из известных ей объектов, если, конечно, такая система интеллектуальна.
То есть ракета не обладает крыльями (x1 = 0), обладает хвостом (x2 = 1), не обладает клювом (x3 = 0), имеет двигатели (x4 = 1), не обладает оперением (x5 = 0), не имеет шасси (x6 = 0).
|
После умножения вектора (010100) на уже обученную матрицу ИС получаем вектор демонов (-2, 0 -1), то есть ракета опознается как самолет (класс Y2), что в принципе верно. Уверенность опознания при этом системы снизилась, например, расстояние между планером и самолетом равно 1.
Построив рисунок, найдите, где в мире находится ракета. Птица – Самолет = (1, 1, 1, 0, 1, 0) - (1, 1, 0, 1, 0, 1) = 4 Птица – Планер = (1, 1, 1, 0, 1, 0) - (1, 1, 0, 0, 0, 0) = 2 Самолет – Планер = (1, 1, 0, 1, 0, 1) - (1, 1, 0, 0, 0, 0) = 2 Птица - Ракета = (1, 1, 1, 0, 1, 0) – (0, 1, 0, 1, 0, 0) = 4 Самолет – Ракета = (1, 1, 0, 1, 0, 1) – (0, 1, 0, 1, 0, 0) = 2 Планер – Ракета = (1, 1, 0, 0, 0, 0) – (0, 1, 0, 1, 0, 0) = 2 Проведите на рисунке циркулем вычисленные расстояния от центров соответствующих классов и найдите место, где пересекаются эти окружности.
|
|
| Рисунок – Представление о мире прогнозируемых объектов в построенной модели в сознании ИС |
Примечания
Следствие 1. Некоторые переменные оказывают существенно большее воздействие на выбор некоего исхода, чем другие. И наоборот некоторые переменные, как несущественные, можно исключить. Например, x1 (крылья), x2 (хвост) – признаки не существенные, так как присутствуют у всех классов.
Следствие 2. Если некоторые переменные не определены, то их значение может быть приравнено 0,5. В этом случае экспертиза затрудняется, так как расстояние между примерами уменьшается, но различие можно установить по оставшимся точным значениям других признаков.
Следствие 3. Систему следует доучивать, если в режиме экспертизы она ошибается. При переучивании может возникнуть также эффект ошибочного опознания классов, которые ранее опознавались правильно. После дообучения следует снова проверить работу системы на всех примерах, которым ее обучали, так как в процессе переучивания (доучивания) система может забывать какие-то примеры.
Следствие 4. Если объект находится вблизи разделяющей плоскости (малые значения демонов), то система может его перепутать с другими объектами.
Объект может легко переместиться через границу в соседний класс, если он находится вблизи границы классов, а, значит, он может быть неправильно распознан.
Следствие 5. Приведем геометрическую интерпретацию полученной модели (матрицы ЭС) ИС.
| -1 | -1 | 0 |
| -1 | -1 | 0 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
| 1 | -1 | -1 |
| -1 | 1 | -1 |
Найденные уравнения системы имеют вид:
|
Y1 = a11*x1 + a12*x2 + a13*x3 + a14*x4 + a15*x5 + a16*x6
Y2 = a21*x1 + a22*x2 + a23*x3 + a24*x4 + a25*x5 + a26*x6
Y3 = a31*x1 + a32*x2 + a33*x3 + a34*x4 + a35*x5 + a36*x6
Или конкретно в числах, подставив вычисленные коэффициенты aij из обученной матрицы:
Y1 = -x1 - x2 + x3 - x4 + x5 - x6
Y2 = -x1 - x2 - x3 + x4 - x5 + x6
Y3 = -x3 - x4 - x5 - x6
Уравнения представляют собой геометрически гиперплоскости в шестимерном гиперпространстве признаков. Одно уравнение – одна гиперплоскость. Плоскости делят пространство на полупространства (в одной части полупространства - Y > 0, в другой – Y < 0, на границе Y = 0). Пересечение гиперплоскостей образует гипертела – классы (класс «птицы», класс «самолеты», класс «планеры»).
Значения коэффициентов уравнений, которые подбирает система для разделения классов, изменяются, то есть гиперплоскости в процессе обучения вращаются и перемещаются. Изменение положения гиперплоскостей происходит таким образом, чтобы они встали, максимально четко разделив области (классы) друг от друга, – посредине между классами.
Чтобы наглядно увидеть геометрическую иллюстрацию уравнений ИС на плоскости листа, спроецируем шестимерное гиперпространство на двухмерную плоскость.
Например, рассматривая две оси: x3 (клюв) и x4 (двигатель), можно изобразить след разделяющей поверхности на плоскости [x3 (клюв), x4 (двигатель)]:
Y1 = ... + x3 - x4 + ...
Y2 = ... - x3 + x4 + ...
Y3 = ... - x3 - x4 + ...
Уравнение для Y1: x3 - x4 = 0 или x3 = x4. На этой линии расположены точки, удовлетворяющие уравнению Y1 = 0. Такая прямая (гиперплоскость) называется разделяющим правилом, так как по одну ее сторону расположены одни классы, а по другую – другие классы.
Класс Y1 (птица) расположен в точке (x3 = 1, x4 = 0, то есть «клюв есть», «двигателя нет»). Класс Y2 (самолет) расположен в точке (x3 = 0, x4 = 1, то есть «клюва нет», «двигатель есть»). Поставим на осях эти точки с указанными координатами.
Разделяющая линия x3 = x4 проведена так, что находится на максимальном удалении от обоих классов, что обеспечивает им максимальное различение системой (расстояние до разделяющей линии). Расстояние от экземпляра класса до разделительной линии – значение демона.
|
|
| Рисунок – Геометрическая интерпретация экспертной системы (уравнение Y1=0 и полуплоскости: Y1>0 – класс «Птицы», Y1<0 – класс «Самолеты») в проекции на систему координат (Х4 – двигатель, Х3 - клюв) |
Следствие 6. Однако, следует понимать, что в классе Птиц, например, могут быть достаточно экзотические экземпляры с нетипичными значениями (x3, x4), которые системой могут быть ошибочно опознаны как Самолеты. Эти объекты могут перейти через разделяющее правило Y1 в полупространство соседнего класса. В этих случаях ИС необходимо доучивать. В процессе дообучения экспертной системы дополнительным экзотическим примерам разделяющие плоскости будут продолжать поворачиваться и смещаться, чтобы еще лучше разделить классы между собой с учетом оригинальных экземпляров.
Следствие 7. Во время обучения у ИС меняются значения коэффициентов aij – то есть разделяющие гиперплоскости вращаются и сдвигаются (коэффициенты влияют на наклон гиперплоскостей к осям пространства).
Обучение (перемещение плоскостей) происходит до тех пор, пока все примеры не будут правильно опознаны, то есть плоскости не встанут так, чтобы все экземпляры каждого класса оказались в своих полупространствах.
Следствие 8. Если система ошибается то в одних примерах, то (при доучивании) в других, это говорит о большом размере шага обучения. Перед сложением/вычитанием вектора-примера к (из) столбцам матрицы имеет смысл умножить весь вектор на шаг h < 1. Если система «тупит», если ей приходится повторять один и тот же пример много раз для того, чтобы существенно подвинулись границы классов, то шаг h надо увеличить.
![]() Шаг h играет здесь роль коэффициента темперамента.
Шаг h играет здесь роль коэффициента темперамента.
Следствие 9. Чем больше значение демона, тем дальше объект находится от разделяющей плоскости, тем четче ИС опознает этот объект, относя его к определенному классу.
По правилу Y1 самолет (0, 1) от планера (0, 0) отличается настолько же, насколько от птицы (0, 1). По правилам Y1 и Y2 точно идентифицировать планер в осях x3 и x4 нельзя (он не относится ни к самолету, ни к птице), точка (x3 = 0, x4 = 0) находится на границе раздела.
Правило Y3 достаточно слабое, так как при предъявлении ему самолета и птицы оно их не различает (Y3 = -1), оба класса находятся по одну сторону от разделяющей линии Y3.
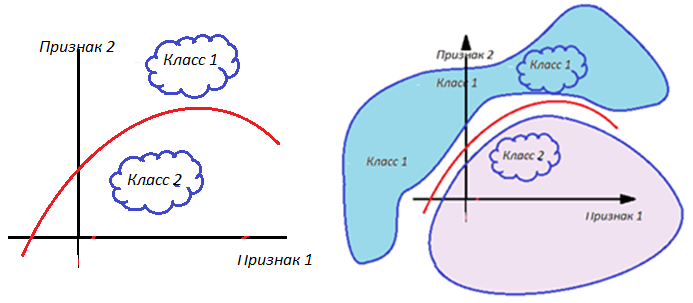
На рисунке показан эскиз, как могли бы выглядеть разделяющие правила Yi, области – классы (Y1 > 0 И Y2 < 0 И Y3 > 0 и т.п.) в проекции на некоторое пространство, образованное признаками 1 и 2.
![]() Признаки – оси координат многомерного пространства. Свойства – значения на шкале признаков. Экземпляры – примеры, точки в пространстве признаков. Линии – границы классов, разделяющие правила, уравнения, причинно-следственные отношения. Области – классы. Каждая точка системой гиперплоскостей {Y} отнесена к конкретной области, классу.
Признаки – оси координат многомерного пространства. Свойства – значения на шкале признаков. Экземпляры – примеры, точки в пространстве признаков. Линии – границы классов, разделяющие правила, уравнения, причинно-следственные отношения. Области – классы. Каждая точка системой гиперплоскостей {Y} отнесена к конкретной области, классу.
|
|
| Рисунок – Геометрическая интерпретация экспертной системы, состоящей из нескольких классов, ограниченных разделяющими правилами (уравнениями Yj), в проекции на оси Признаков (Хi). (Проверьте расстояние (демона) от отдельного экземпляра одного из классов до всех возможных правил) |
Имейте в виду:
1. удаленные примеры оттягивают на себя поверхность раздела классов,
2. объекты вблизи поверхности раздела нечетки и могут быть ложно классифицированы,
3. некоторые переменные оказывают бо’льшее влияние на результат, чем другие (что следует учитывать при ранжировании вопросов, предъявляемых интеллектуальной системой пользователю при экспертизе),
4. некоторые переменные вообще не влияют на результат (и их надо исключить из экспертизы как неинформативные) – крылья есть и у птицы, и самолета, и у планера,
5. нормализация ИС – выбор пользователя,
6. на скорость обучения ИС существенно влияет величина шага обучения (малый шаг – система обучается медленно, проявляя тупость, консерватизм, большой шаг – соответствует разболтке системы, проявляя дурость, авантюризм),
7. переменные могут принимать непрерывные значения, сигнализируя о четкости наблюдения конкретного признака,
8. несколько ИС могут быть объединены в единую систему путем слияния матриц.
Уточнения. При борьбе с неудачами при настройке ИС можно использовать следующие приемы, известные из курса «Моделирование систем»:
1. Вводят дополнительный признак. Увеличение размерности пространства позволяет решить проблему Минского (исключающее ИЛИ). То, что нельзя разделить в плоскости прямой линией, можно разделить в пространстве выше размерностью плоскостью.
|
|
| Рисунок – Введение дополнительной переменной z позволило отделить плоскостью (линейной формой) сиреневые точки от синих |
2. Слишком широкий класс разбивают на подклассы. Увеличение количества подпространств, дробление гипертел позволяет упростить задачу построения модели за счет линеаризации описываемых областей. Например, класс «Аисты» можно разбить на два класса «Черные аисты» и «Белые аисты».
|
|
| Рисунок – Два класса друг от друга можно отделить нелинейной границей |
|
|
| Рисунок – Преобразование одного класса «Класс 1» в два класса «Класс 1А» и «Класс 1Б». Границы классов становятся линейными |
3. Линейную систему переводят в нелинейную, дополняя ее уравнение нелинейными членами. Это позволяет некоторые экзотические примеры вблизи раздела сред обойти плавными непрямыми линиями. Прием соответствует введению связей между признаками.
Например так: Y = … + x3 + x4 + x3*x4 + x32 + x42 + …
|
|
| Рисунок – Сиреневые точки отделены от синих нелинейной функцией |
Генетическая связь экспертной системы и регрессионной модели
Посмотрим на задачу с другой стороны. Итак, исходные данные… Таблица – Исходная база данных
| Крылья, X1 | Хвост, X2 | Клюв, X3 | Двигатель, X4 | Оперение, X5 | Шасси, X6 | |
| Птица, Y1 | 1 | 1 | 1 | 0 | 1 | 0 |
| Самолет, Y2 | 1 | 1 | 0 | 1 | 0 | 1 |
| Планер, Y3 | 1 | 1 | 0 | 0 | 0 | 0 |
Внимательно посмотрев, можно увидеть, что столбик Х3 повторяет столбик Х5. Таким образом, один из признаков дублирует полностью другой и одним из них можно пренебречь. Также дублируются столбцы Х4 и Х6. Столбцы Х1 и Х2 также дублируются.
Сожмем базу данных. Таблица – Сжатая база данных
| Значение Y | Крылья, X1 Хвост, X2 | Клюв, X3 Оперение, X5 | Двигатель, X4 Шасси, X6 | |
| Птица, Y1 | 0 | 1 | 1 | 0 |
| Самолет, Y2 | 8 | 1 | 0 | 1 |
| Планер, Y3 | 4 | 1 | 0 | 0 |
Составим модель.
1. Для этого закодируем признак Y - переведем его из качественной области (птица, самолет, планер) в количественную (0, 8, 4). Логично, что планер находится где-то между птицей и самолетом, как мы это ранее выяснили.
2. Допустим, что модель имеет линейный характер: Y = a*X1 + b*X3 + c*X4 + d.
Для нахождения коэффициентов (a, b, c, d) составим систему уравнений, используя базу данных для всех трех строк:
|
Отсюда немедленно получаем результат: a = 4, b = -4, c = 4, d = 0.
Или Y = 4*X1 - 4*X3 + 4*X4 (линия трендов).
Проверка. При Х1 = 1, Х3 = 1, Х4 = 0 получаем Y = 0, то есть при наличии крыльев Х1 или хвоста Х2, наличии клюва Х3 или оперения Х5, отсутствии двигателя Х4 или шасси Х6 уравнение соответствует значению Птица.
При Х1 = 1, Х3 = 0, Х4 = 1 получаем Y = 8, то есть при наличии крыльев Х1 или хвоста Х2, отсутствии клюва Х3 или оперения Х5, наличии двигателя Х4 или шасси Х6 уравнение соответствует значению Самолет.
При Х1 = 1, Х3 = 0, Х4 = 0 получаем Y = 4, то есть при наличии крыльев Х1 или хвоста Х2, отсутствии клюва Х3 или оперения Х5, отсутствии двигателя Х4 или шасси Х6 уравнение соответствует значению Планер.
При подстановке Ракеты (Х2 = 1, Х4 = 1) получаем Y = 4*0 - 4*0 + 4*1 = 4 (планер), что не соответствует истине.
На рисунке в осях X1, X3, X4 изображена плоскость Y = 4*X1 - 4*X3 + 4*X4 при различных значениях Y = 0,4,8. Видно, что плоскость 4*X1 - 4*X3 + 4*X4 = 0 проходит через точку Птица (1, 1, 0). Плоскость 4*X1 - 4*X3 + 4*X4 = 4 проходит через точку Планер (1, 0, 0). Плоскость 4*X1 - 4*X3 + 4*X4 = 8 проходит через точку Самолет (1, 0, 1).
|
|
| Рисунок – Геометрическая иллюстрация уравнения Y = 4*X1 - 4*X3 + 4*X4 экспертной системы в трех осях координат {X1, X3, X4} |
Заметим, что столбцы Х1 и Х2 не только дублируют друг друга, но от них вообще ничего не зависит, у всех классов всегда есть крылья и хвост. Это вообще неинформативные признаки, не дифференцирующие, с помощью их ничего от чего-то другого отличить нельзя. Исключаем столбцы Х1 и Х2 из базы данных.
Исходные данные для построения модели упрощаются. Таблица – Максимально сжатая база данных
| Значение Y | Клюв, X3 Оперение, X5 | Двигатель, X4 Шасси, X6 | |
| Птица, Y1 | 0 | 1 | 0 |
| Самолет, Y2 | 8 | 0 | 1 |
| Планер, Y3 | 4 | 0 | 0 |
Ищем уравнение в линейном виде: Y = a*X3 + b*X4 + d.
Для этого составим три уравнения, исходя из трех строк базы данных.
|
Решая систему уравнений, получаем: a = -4, b = 4, d = 4.
Или Y = -4*X3 + 4*X4 + 4.
Проверка модели. При Х3 = 1 (есть клюв или оперение) и Х4 = 0 (нет двигателя или шасси) имеем Y = 0 (птица). При Х3 = 0 (нет клюва или оперения) и Х4 = 1 (есть двигатель или шасси) имеем Y = 8 (самолет). При Х3 = 0 (нет клюва или оперения) и Х4 = 0 (нет двигателя или шасси) имеем Y = 4 (планер). Ракета (Х3 = 0, Х4 = 1) опознается как самолет (Y = 8), что верно.
Проиллюстрируем геометрически полученную модель. Поставим точки (записи базы данных, экземпляры, числа), используя их координаты, на оси Х3 и Х4 – птица (0, 1), самолет (1, 0), планер (0, 0).
Изобразим прямую линию Y = -4*X3 + 4*X4 + 4 для разных значений Y = {0, 4, 8} в виде семейства параллельных прямых. При Y = 0 имеем: 0 = -4*Х3 + 4*Х4 + 4 или Х3 = Х4 + 1. При Y = 4 имеем: 4 = -4*Х3+4*Х4 + 4 или Х3 = Х4. При Y = 8 имеем 8 = -4*X3 + 4*X4 + 4 или Х3 = Х4 - 1.
|
|
| Рисунок – Геометрическая интерпретация регрессионной модели Y = -4*X3 + 4*X4 + 4 – след плоскости в двух осях координат |
|
|
| Рисунок – Геометрическая интерпретация регрессионной модели – плоскость в трех осях координат, разметка осей (справа) |
Видно, что при Y = 0 значение класса Y соответствует Птице. При Y = 4 – классу Планер. При Y = 8 – классу Самолет.
Отметим, что расстояние от класса Птица до класса Планер равно 4 по Y, от Планера до Самолета равно 4 по Y (оранжевый треугольник), между классами Птица и Самолет расстояние Y=8, что соответствует ранее построенному качественному рисунку.
|
|
| Рисунок – Геометрическая интерпретация качественного положения экземпляров (справа) и рассчитанного численно по регрессионной модели (слева) |
Заметим, что если кодировку проделать иначе, то уравнение будет другого вида. Рассмотрим пример для новой кодировки. Таблица – Перекодированная и максимально сжатая база данных
| Значение Y | Клюв, X3 Оперение, X5 | Двигатель, X4 Шасси, X6 | |
| Птица, Y1 | 8 | 1 | 0 |
| Самолет, Y2 | 4 | 0 | 1 |
| Планер, Y3 | 0 | 0 | 0 |
Имеем: Y = 8*X3 + 4*X4.
Примечание. Неудачная кодировка может потянуть за собой необходимость представления модели в виде нелинейного уравнения. Порядок уравнения обусловлен количеством кодируемых классов, то есть значений Y. Так в нашем примере наибольшая степень полинома, описывающего три класса – 2.
|
|
| Рисунок – При неудачной кодировке уравнение может стать нелинейным |
Покажем, как связаны между собой регрессионное уравнение Y = -4*X3 + 4*X4 + 4 и уравнения экспертной системы:
Y1 = -x1 - x2 + x3 - x4 + x5 - x6
Y1 = -x1 - x2 - x3 + x4 - x5 + x6
Y1 = -x3 - x4 - x5 - x6
Убираем лишние Х1 и Х2, сжимаем дубли Х3 и Х5, Х4 и Х6:
Y1 = +x3 - x4
Y2 = -x3 + x4
Y3 = -x3 - x4
Вспомните, мы выбирали класс по признаку: max(Y1, Y2, Y3).
Поскольку, экземпляр Птица находится в области с Y1 > Y2 и Y1 > Y3, а, значит, должны выполняться неравенство Х3 - Х4 > -X3 + X4 и одновременно неравенство X3 - X4 > -X3 - X4. Решая их совместно, получаем, что Птицы занимают область (Х3 > X4)&(X3 > 0) в пространстве осей {Х3, Х4}.
Поскольку, экземпляр Самолет находится в области с Y2 > Y1 и Y2 > Y3, а, значит, -Х3 + Х4 > X3 - X4 и -X3 + X4 > -X3 - X4, то Самолеты занимают область (Х4 > X3)&(X4 > 0) в пространстве осей {Х3, Х4}.
Поскольку, экземпляр Планер находится в области с Y3 > Y1 и Y3 > Y2, а, значит, -Х3 - Х4 > X3 - X4 и -X3 - X4 > -X3 + X4, то Планеры занимают область (Х3 < 0)&(X4 < 0) в пространстве осей {Х3, Х4}.
На рисунке это можно обозначить тремя областями, разделенными тремя линиями-границами. Каждая область – определенный класс. В областях красной точкой показаны типичные экземпляры каждого класса (самолет, птица и планер).
|
|
| Рисунок – Геометрическая иллюстрация результата работы экспертной системы в двух осях координат (клюв - двигатель), видны три области – три класса, синие линии- границы областей, красные точки – экземпляры классов |
Наконец, совмещая две иллюстрации:
- области и границы модели экспертной системы и
- области и границы регрессионной модели,
имеем:
|
|
| Рисунок – Геометрическая интерпретация экспертной системы и регрессионной модели в двух осях, виден след плоскости регрессионной модели |
Y = f(X3, X4) надо представлять себе здесь как плоскость от двух переменных, выдвигающуюся при движении влево вверх на наблюдателя. Y увеличивается перпендикулярно к осям Х4 и Х3 по направлению к наблюдателю. Ниже то же изображение, только плоскость Y = -4*X3 + 4*X4 + 4 регрессионной модели показана трехмерной. Хорошо видны области и их границы (Х3 = Х4, Х4=0, Х3=0) у экспертной системы.
|
|
| Рисунок – Геометрическая интерпретация экспертной системы и регрессионной модели в трех осях, видна плоскость регрессионной модели, видны три области - класса |
Ниже на рисунке приведены с разных ракурсов изображение областей классов и точек экземпляров объектов в 6-мерном пространстве {X1, X2, X3, X4, X5, X6}. Границы классов – 6-мерные гиперплоскости, которые выглядят в проекции на 2-мерное пространство как тела-фигуры. С определенного ракурса гиперплоскость будет иметь вид прямой линии, разделяющей пространство на две полуплоскости (положительную и отрицательную).
Учимся рисовать многомерные пространства и фигуры
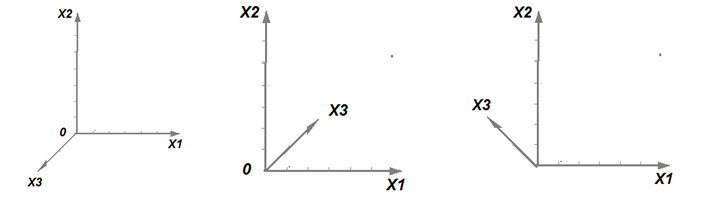
Нарисуем пару координатных осей Х1 и Х2 взаимно перпендикулярно, как это было предложено в свое время Декартом. Третью ось Х3 нарисуем под углом к первым двум осям. Так поступают всегда, когда хотят отобразить трехмерное пространство на плоскость рисунка. При этом направление третьей оси может быть вообще любым. Если менять направление третьей оси в динамике, то можно наблюдать трехмерный объект в разных ракурсов. Это удобно для получения полного представления о нем.
|
|
| Рисунок – Пример различного расположения осей пространства 3D |
Пример 1. Чтобы изобразить точку Т(2,4,-1) в трех осях, достаточно отложить вдоль первой оси расстояние 2 (нарисовать черновик точки Т’), затем вдоль оси Х2 от Т’ отложить расстояние 4 (нарисовать черновик точки Т’’) и далее от точки Т’’ вдоль направления оси Х3 отложить расстояние (-1). Минус означает здесь движение против заданного направления оси. Данное местоположение будет изображением точки Т.
|
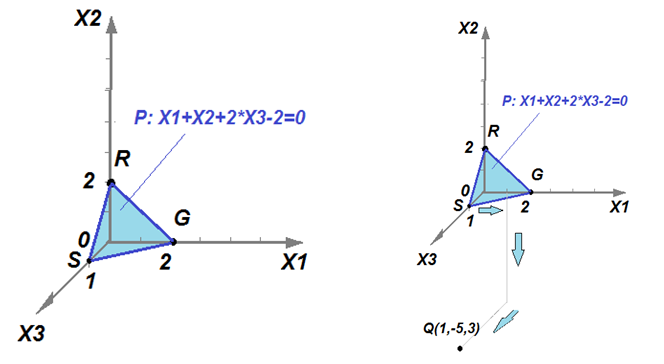
Пример 2. Чтобы изобразить плоскость Р: X1 + X2 + 2*X3 - 2 = 0, надо поставить на рисунок множество точек, каждая из которых при подстановке ее координат в уравнение обращает его левую часть в ноль.
Например, Q(1, -5,3) при подстановке в уравнение дает: 1*1 + 1*(-5) + 2*3 - 2 = 0 (то есть точка Q принадлежит плоскости Р).
Далее нарисовать такую точку в заданных осях. Повторив эту операцию с множеством точек, удовлетворяющих уравнению, увидим изображение плоскости. Поскольку плоскость в трехмерном пространстве задается тремя точками, то достаточно нарисовать только три точки (не совпадающие между собой и не лежащие на одной прямой), соединив их прямыми линиями для наглядности. Часто для простоты вычислений и рисования эти три точки берут на осях координат.
Например, G(2, 0, 0), R(0, 2, 0), S(0, 0, 1) – эти точки подобраны так, что лежат на осях координат и каждая удовлетворяет уравнению, обращая его левую часть в ноль.
Однако надо иметь в виду, что плоскость бесконечная и продолжается за условно обозначенные на рисунке границы во все стороны. Так, например, точка Q(1, -5,3) также принадлежит этой плоскости.
|
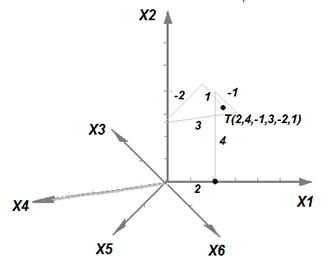
Пример 3. Нарисуем оси 6-мерного пространства. Для этого в любые стороны (как это было с третьей осью) проведите еще три прямые из начала координат.
Нарисуем точку Т(2,4, -1,3, -2,1) в 6-мерном пространстве, продолжая намечать черновик ее изображения еще по четвертой, потом пятой и далее вдоль шестой оси координат. В результате на плоскости листа появится точка Т, установленная в 6-мерном пространстве.
|
Если это проделать с множеством точек, координаты которых удовлетворяют заданному уравнению плоскости (или более сложной фигуры), то вы увидите многомерную фигуру с определенной точки зрения. Если плавно начать менять углы взаимного положения осей, то перед вашим взором начнет вращаться 6-мерная фигура.
Интересно, что 6-мерная плоскость в 2-мерной проекции с разных сторон будет выглядеть чаще как неплоская фигура, как якобы обладающее объемом тело. Но с определенного ракурса она будет выглядеть как прямая линия.
|
|
| Рисунок – Пример найденного ракурса наблюдения, при котором точки 4D гиперплоскости x + y + z + w = 0 выстроились в прямую линию. При произвольной точке наблюдения плоскость выглядит как тело. Однако, если повернуть эту гиперплоскость в двумерных плоскостях yw на угол 45°, yz – на 45°, xw – на 225°, то получится прямая линия при наблюдении на экране. Хорошо видно множество точек, удовлетворяющих уравнению. |
Хорошо видно множество точек, удовлетворяющих уравнению.
Далее на рисунке представлен еще один пример ракурса для более высокой размерности пространства – 6D. Плоскость на рисунке имеет следующее уравнение:
-x + y + z - w + k - d = 0.
|
|
| Рисунок – Пример найденного ракурса наблюдения, при котором фигура 6D гиперплоскости превратилась в прямую линию |
Любая БД – это множество записей, каждая из которых характеризует один экземпляр описываемой предметной области, и может рассматриваться как соответствующее множество точек в пространстве с размерностью, равной количеству атрибутов БД.
На примере показан геометрический образ БД «Iris Dataset» (https://archive.ics.uci.edu/ml/datasets/iris). Оси координат – это выделенные исследователями признаки ирисов в БД – sepal length, sepal width, petal length, petal width, то есть пространство четырехмерное.
Точки на рисунке соответствуют конкретным экземплярам цветов, одна точка- одна запись БД – один экземпляр цветка.
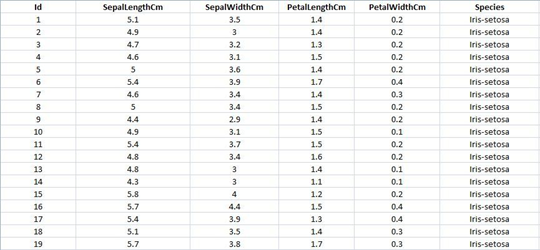
Часть датасета в БД проиллюстрирована на рисунке.
|
|
| Рисунок – Часть Iris Dataset, представленного в виде базы данных |
На данном множестве была обучена экспертная система. Входными данными для экспертной системы являются наборы значений признаков объекта (в данном случае ирисов). На выходе экспертной системы получена система уравнений (алгебраическая модель), которая представляет собой геометрически множество гиперобластей в пространстве N = 4, представляющих 3 класса ирисов (Iris Setosa, Iris Versicolour, Iris Virginica). Гиперобласти отделяются друг от друга гиперплоскостями, которые можно визуализировать. Точки в многомерном пространстве представляют собой конкретные экземпляры классифицируемых множеств объектов.
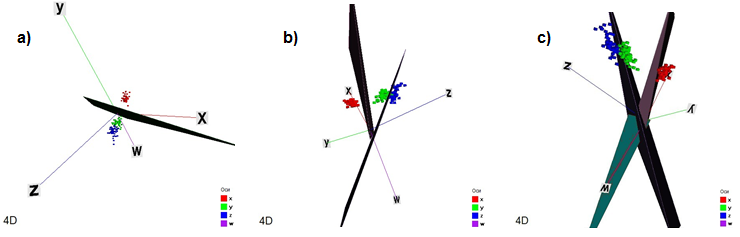
На рисунке приведен образ трех уравнений (гиперплоскостей) в четырехмерном пространстве признаков:
y1 = 0.606971x + 2.26988y - 3.73073z - 0.906969w;
y2 = -0.254227x - 2.93349y + 3.30889z - 7.06086w;
y3 = -5.91036x - 5.07457y + 9.06865z + 8.20968w;
|
|
| Рисунок – Закономерности, найденные экспертной системой и наблюдаемые с различных трехмерных ракурсов в плоскости монитора (a – видна одна гиперплоскость w1 в виде тела, b – видны две гиперплоскости w1, w2, каждая с «торца», с – видны три гиперплоскости w1, w2, w3) |
При проецировании 4-мерных плоскостей в 3-мерное пространство эти плоскости для наблюдателя принимают форму объемных фигур. При определенном угле поворота точки взгляда наблюдателя гиперплоскость можно увидеть «с торца», то есть увидеть прямую. В таком положении исследователь получает возможность увидеть разделение классов гиперплоскостями (правилами, порождаемыми экспертной системой).
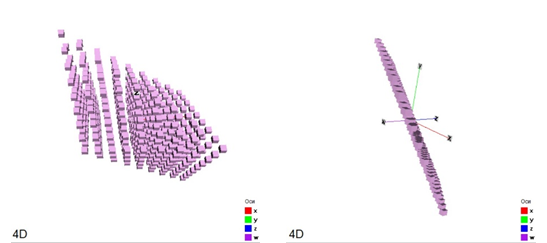
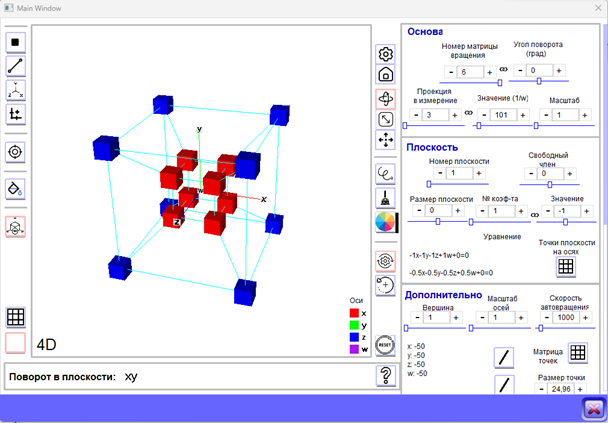
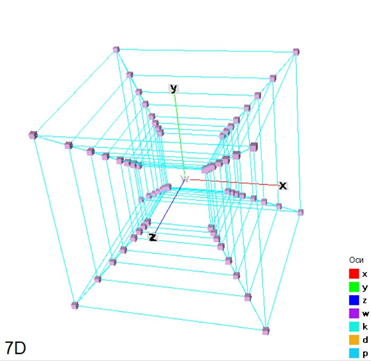
На рисунках для примера показаны многомерные куб и сфера. В углу рисунка указана размерность пространства.
|
|
| Рисунок – Четырехмерный куб. Построение дополнено ребрами, соединяющими вершины куба |
|
|
| Рисунок – 7-мерный куб |
|
|
| Рисунок – Четырехмерная сфера, построенная их точек, координаты которых удовлетворяют уравнению сферы с центром в начале координат: x2 + y2 + z2 + w2 = 0 |
|
|
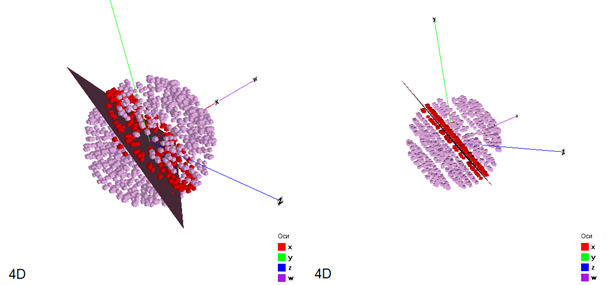
| Рисунок – Сфера, пересекаемая плоскостью C: x + y + z + w = 0 (сфера состоит из точек, принадлежащей «истинной» сфере, телу). Здесь красные точки принадлежат секущей плоскости |
|
|
| Рисунок – Сфера, секущая плоскость и сечение сферы в 4D. При повороте сферы на угол 45 град. в плоскости XW, ее сечение превратиться в «плоское» |
В дальнейшем после знакомства с другими методами искусственного интеллекта можно будет представить ответ этой задачи на языке логики, языке нейронной сети или дерева ID3. Ниже на рисунках показаны соответствующие реализации.
На языке логических функций: Птица := X3 ИЛИ Х5 Самолет := Х4 ИЛИ Х6 Планер := НЕ (Х3 ИЛИ Х5) И НЕ (Х4 ИЛИ Х6)
Более формально: Птица := x3 ∨ x5 Самолет := x4 ∨ x6 Планер := ¬ x3 & ¬ x4 & ¬ x5 & ¬ x6
На языке деревьев ID3:
|
|
| Рисунок – Индуктивное дерево решений, построенное методом ID3 |
На языке нейросетей (разные варианты реализации):
|
|
| Рисунок – Схема «дискретной» нейронной сети на ступенчатых нейронах с порогом равным нулю |
|
|
| Рисунок – Схема «аналоговой» нейронной сети на ReLU-нейронах, которая реализует уравнение Y = -4*X3 + 4*X4 + 4 |
Задание.
Возьмите за основу известную Вам классификацию (не менее 6-8 классов, не менее 7-8 признаков).
Известные примеры:
- музыкальные инструменты,
- кулинарные рецепты,
- болезни человека и их симптомы,
- Устав сухопутных войск (диспозиция войск на местности и решения военачальников),
- транспортные машины,
- одежда, одеваемая нами в зависимости от погоды,
- классификация животных,
- классы комбинаций игры в покер и так далее.
Опишите классы и признаки.
Предъявляя модели экспертной системы примеры на классифицирование, проимитируйте несколько актов обучения. Рассчитайте и приведите вид матриц.
Пример построения экспертной системы Вы найдете в книге [3].
Переведите систему в режим экспертизы. Проведите экспертизу всех тех классов, которые предъявлялись экспертной системе.
Если экспертиза проходит с ошибками, вернитесь в режим обучения и дообучите систему. Добейтесь того, что система перестанет ошибаться на всех предложенных ей примерах.
Предъявите ранее неизвестный ей класс (задача прогноза). Опишите результаты экспертизы. Приведите вид матриц. Приведите вид полученной модели (систему уравнений) и ее геометрическую иллюстрацию.
Оцените результат обучения, эффективность процедуры (адекватность системы), характер и причины ошибок, кривую обучения (количество ошибок в зависимости от номера итерации обучения).
Задание для исследователей:
Обучите систему с нуля при разных значениях шага. Сделайте вывод.
Приведите вид изменяющейся в процессе обучения модели (систему уравнений) и геометрическую иллюстрацию.
Заключение «Что мы уже узнали».
Практика 1 – правило (оценочную функцию) мы задали сами, компьютер играл вспомогательную роль вычислителя. Доказано, что можно руководствуясь правилом (моделью), прийти к цели, не зная точного описания и подробностей алгоритма решения. Решающей характеристикой правила является его кпд. На кпд влияет коэффициент темперамента. Коэффициент темперамента – соотношение консерватизма (сохранения, пассивности) и авантюризма (развития, агрессии) при принятии решений. В конце практики обсудили вопрос о том, как повысить интеллектуальность компьютера, поручив ему перебирать числовые коэффициенты правила случайно или подряд.
Практика 2 – попытка настроить числовые коэффициенты правил наилучшим образом автоматически, то есть передать компьютеру часть функций естественного интеллекта. Само правило пока все равно задано нами (Демиургом). Можно, конечно, задать изначально избыточно сложное правило (нелинейное высокой размерности). Тогда вычисленные коэффициенты со значениями около нуля укажут на избыточность отдельных частей правил.
| О руководителе курса «Моделирование систем» | Лекция 02. Линейные регрессионные модели | ||||||||||||||||
|
|||||||||||||||||


![[ Рис. Расположение объектов в мире, как есть ] [ Рис. Расположение объектов в мире, как есть ]](lection38/img06.png)
![[ Рис. Расположение объектов в сознании интеллектуальной системы, как ИС представляет окружающий мир через обучение ] [ Рис. Расположение объектов в сознании интеллектуальной системы, как ИС представляет окружающий мир через обучение ]](lection38/img07.png)

![[ Рис. Представление о мире прогнозируемых объектов в построенной модели в сознании ИС ] [ Рис. Представление о мире прогнозируемых объектов в построенной модели в сознании ИС ]](lection38/img09.png)
![[ Рис. Геометрическая интерпретация экспертной системы в проекции на систему координат ] [ Рис. Геометрическая интерпретация экспертной системы в проекции на систему координат ]](lection38/img11.png)
![[ Рис. Геометрическая интерпретация экспертной системы, состоящей из нескольких классов, ограниченных разделяющими правилами в проекции на оси Признаков ] [ Рис. Геометрическая интерпретация экспертной системы, состоящей из нескольких классов, ограниченных разделяющими правилами в проекции на оси Признаков ]](lection38/img12.png)
![[ Рис. Введение дополнительной переменной z позволило отделить плоскостью (линейной формой) сиреневые точки от синих ] [ Рис. Введение дополнительной переменной z позволило отделить плоскостью (линейной формой) сиреневые точки от синих ]](lection38/img13.png)

![[ Рис. Сиреневые точки отделены от синих нелинейной функцией ] [ Рис. Сиреневые точки отделены от синих нелинейной функцией ]](lection38/img17.png)
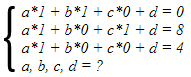
![[ Рис. Геометрическая иллюстрация уравнения экспертной системы в трех осях координат ] [ Рис. Геометрическая иллюстрация уравнения экспертной системы в трех осях координат ]](lection38/img19.png)

![[ Рис. Геометрическая интерпретация регрессионной модели след плоскости в двух осях координат ] [ Рис. Геометрическая интерпретация регрессионной модели след плоскости в двух осях координат ]](lection38/img21.png)
![[ Рис. Геометрическая интерпретация регрессионной модели – плоскость в трех осях координат, разметка осей (справа) ] [ Рис. Геометрическая интерпретация регрессионной модели – плоскость в трех осях координат, разметка осей (справа) ]](lection38/img22.png)
![[ Рис. Геометрическая интерпретация качественного положения экземпляров (справа) и рассчитанного численно по регрессионной модели (слева) ] [ Рис. Геометрическая интерпретация качественного положения экземпляров (справа) и рассчитанного численно по регрессионной модели (слева) ]](lection38/img23.png)
![[ Рис. При неудачной кодировке уравнение может стать нелинейным ] [ Рис. При неудачной кодировке уравнение может стать нелинейным ]](lection38/img24.png)
![[ Рис. Геометрическая иллюстрация результата работы экспертной системы в двух осях координат (клюв - двигатель), видны три области – три класса, синие линии- границы областей, красные точки – экземпляры классов ] [ Рис. Геометрическая иллюстрация результата работы экспертной системы в двух осях координат (клюв - двигатель), видны три области – три класса, синие линии- границы областей, красные точки – экземпляры классов ]](lection38/img25.png)
![[ Рис. Геометрическая интерпретация экспертной системы и регрессионной модели в двух осях, виден след плоскости регрессионной модели ] [ Рис. Геометрическая интерпретация экспертной системы и регрессионной модели в двух осях, виден след плоскости регрессионной модели ]](lection38/img26.png)
![[ Рис. Геометрическая интерпретация экспертной системы и регрессионной модели в трех осях, видна плоскость регрессионной модели, видны три области - класса ] [ Рис. Геометрическая интерпретация экспертной системы и регрессионной модели в трех осях, видна плоскость регрессионной модели, видны три области - класса ]](lection38/img27.png)




![[ Рис. Индуктивное дерево решений, построенное методом ID3 ] [ Рис. Индуктивное дерево решений, построенное методом ID3 ]](lection38/img28.png)
![[ Рис. Схема «дискретной» нейронной сети на ступенчатых нейронах с порогом равным нулю ] [ Рис. Схема «дискретной» нейронной сети на ступенчатых нейронах с порогом равным нулю ]](lection38/img29.png)
![[ Рис. Схема «аналоговой» нейронной сети на ReLU-нейронах ] [ Рис. Схема «аналоговой» нейронной сети на ReLU-нейронах ]](lection38/img30.png)