 |
 |
|
Введение
|
|
|
| Таблица 1 – Классификация языков по уровню |
![[ Таблица 1 – Классификация языков по уровню ]](lection37/img01.png "[ Таблица 1 – Классификация языков по уровню ]")
Мы говорим, «что» надо сделать, а ИС сама решает «как» надо сделать и делает это. (Следующий уровень интеллектуальности, когда ИС решает за нас, что надо сделать, видимо, является крайне опасным).
Это удобно, это упрощает нашу работу, поскольку уменьшает наши затраты и, значит, повышает кпд. А повышение кпд – есть задача автоматизации, и вообще задача общественного развития – «меньше затрачивать, больше получать результатов». По определению:
КПД = Результат/Затраты.
Рассмотрим на примере работу таких интеллектуальных систем.
Цель работы – проверить гипотезу о том, что система может найти рациональное решение в бесконечно сложной среде, имея достаточно простое правило, не имея подробного алгоритма, предоставленного кем-то.
Описание задачи «Восьмяшки»
В матрице 3 на 3 расположены 8 фишек, каждая имеет номер от 1 до 8. Одно место в матрице не занято. Любую фишку можно передвинуть (влево, вправо, вниз, вверх), если рядом есть свободное место. Сначала фишки в матрице расположены произвольным образом. Необходимо добиться заданного положения фишек в матрице. За один ход можно передвинуть только одну фишку.
Головоломка «Пятнашки» с матрицей 4 на 4 придумана С. Ллойдом, а рассматриваемый пример для матрицы 3 на 3 использовал Н. Нильсон.
Пусть исходное состояние матрицы будет таким:
| 2 | 4 | 3 |
| 1 | 8 | 5 |
| 7 | 6 |
Зададим цель – конечное (целевое) состояние матрицы:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 |
Задача ИС перейти от исходного состояния к целевому. Это возможно за некоторое (неизвестное заранее) количество шагов.
|
Порядок шагов от исходного состояния к цели – траектория решения задачи, которую надо найти.
Траекторию (как решить задачу) должна найти сама ИС, мы лишь сообщим ей, чего именно нам надо достичь.
Объясним компьютеру, «что такое хорошо» и «что такое плохо». Фактически мы сообщаем критерий, по которому компьютер будет производить отбор решений из возможных по правилам игры, которые играют роль ограничений.
«Хорошо» – это если все фишки стоят на своих местах, как в целевой матрице. «Хуже», если несколько фишек стоит не на своих местах и совсем «плохо», если все фишки не на местах. То есть, мы таким образом задали возможность сравнения локальных действий (решений) – очень хорошо, хорошо, плохо, очень плохо – ввели шкалу. Научились сравнивать, научились измерять!!
Полезное пояснение. По сути, это правило напоминает компас. Если у Вас есть компас, Вы находитесь в комнате и хотите попасть на Северный полюс, то, пользуясь компасом, Вы можете судить в целом: в том ли направлении Вы движетесь. Однако, это не значит, что Вы пойдете строго по стрелке компаса, из-за того, что в комнате есть стены, окна, двери, Вам придется иногда двигаться даже в обратном направлении от Севера. Однако, что интересно, на Северный полюс Вы придете.
Итак, мы, Боги, во-первых, введем норму несогласованности матриц, расстояние между состояниями G – количество фишек, находящихся не на своих местах в матрице. Это дает возможность компьютеру оценивать расстояние до конечного результата, а, следовательно, судить, выбирая каждый раз тот или иной ход, - в правильном направлении или нет происходит движение, имеет место улучшение результата или нет.
Очевидно, что G – плохо, поэтому G -> min.
Но путей к цели может быть много, поэтому среди них должен быть выбор (одни пути чем-то хуже, другие – лучше). Значит…
Во-вторых, желательно прийти к цели побыстрее, может быть даже наикратчайшим путем. Обозначим, H – количество шагов, необходимое для достижения цели, которое тоже желательно иметь небольшой величиной. Очевидно, что Н – плохо, поэтому Н -> min.
Чтобы свести два критерия к одной величине, свернем их одним из известных способов в один и сформулируем общий критерий поиска лучшего хода.
Предлагается минимизировать величину F = G + H -> min.
Такую величину называют в играх тактикой. Следует заметить, что если тактика неудачная, то она может не привести к результату.
Обратите внимание: критерий «что такое хорошо и что такое плохо», 2 противоборствующих фактора (время и место целеположения), генерация области возможных решений (расширение), отбор в области возможных решений (сужение).
Из каждого состояния матрицы можно сделать, очевидно, несколько вариантов хода (множество допустимых правилами игры решений, это задается ограничениями мира). Поэтому возможные ходы можно представить в виде дерева, в котором позднее надо будет отыскать наилучшую последовательность ходов.
Постановка задачи и ее решение напоминает действия с компасом. Компас декларирует правило: «Иди по стрелке, попадешь на север». Находясь в комнате, мы не сможем двигаться по стрелке компаса точно на север (мешают стены), но двигаясь по равнодействующей (компромисс между «что надо» и «что можно»), мы можем выйти в двери, спуститься по лестнице, выйти на улицу, пройти по полю, обогнуть овраги и … прийти на Северный полюс. Алгоритм не задан, задано правило. Окружающая среда сложна и непредсказуема. Однако решение находится.
Ход 0 (H = 0).
Из исходного положения
| 2 | 4 | 3 |
| 1 | 8 | 5 |
| 7 | 6 |
| 2 | 4 | 3 |
| 1 | 8 | 5 |
| 7 | 6 |
Фишка «7» идет вправо. На своем месте только фишка «3». То есть не на своем месте стоит 8 фишек из девяти. G = 8. H = 0. F = G + H = 8
| 2 | 4 | 3 |
| 1 | 5 | |
| 7 | 8 | 6 |
Фишка «8» идет вниз. На своем месте 3 фишки «3, 7, 8». То есть не на своем месте стоит 6 фишек из девяти. G=6. H=0. F = G + H = 6
| 2 | 4 | 3 |
| 1 | 8 | 5 |
| 7 | 6 |
Фишка «6» идет влево. На своем месте 3 фишки «3, 7, пусто». То есть не на своем месте стоит 6 фишек из девяти. G=6. H=0. F = G + H = 6
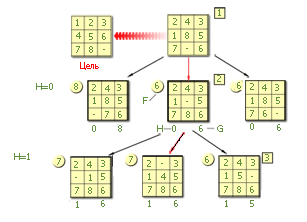
Если просматривать дерево слева направо, то лучшим из рассмотренных ходов (смотри наименьшее значение критерия F) для дальнейшего рассмотрения является вторая матрица с оценкой F=6. Поэтому, пока нет матрицы с лучшей оценкой, чем F=6, то будем развивать дерево из этой матрицы-вершины. В дереве она помечается как вершина N=2 (полученная второй). Первой (N=1) является исходная матрица.
|
Ход 1 (H = 1).
Из получившегося положения возможно 3 варианта хода, результатом которых будут следующие матрицы:
| 2 | 4 | 3 |
| 1 | 5 | |
| 7 | 8 | 6 |
Фишка «1» идет вправо. На своем месте 3 фишки «3, 7, 8». То есть не на своем месте стоит 6 фишек из девяти. G=6. H=1. F = G + H = 7
| 2 | 3 | |
| 1 | 4 | 5 |
| 7 | 8 | 6 |
Фишка «4» идет вниз. На своем месте 3 фишки «3, 7, 8». То есть не на своем месте стоит 6 фишек из девяти. G=6. H=1. F = G + H = 7
| 2 | 4 | 3 |
| 1 | 5 | |
| 7 | 8 | 6 |
Фишка «5» идет влево. На своем месте 4 фишки «3, 5, 7, 8». То есть не на своем месте стоит 5 фишек из девяти. G=5. H=1. F = G + H = 6
Если просматривать дерево слева направо, то самой перспективной для дальнейшего рассмотрения будет именно эта последняя вершина (F=6). В дереве она помечается как вершина N=3 (полученная третьей).
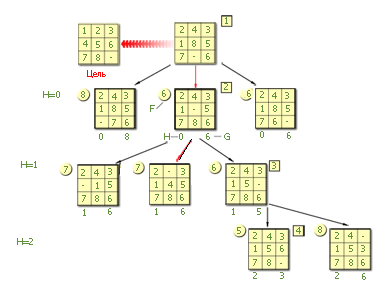
Дерево игры сейчас выглядит таким образом:
|
Среди возможных для продолжения игры вершин, а их всего 5 (область допустимых решений – крона дерева, листья дерева) самой перспективной следует признать ту, которая имеет наименьшее значение критерия F. То есть среди F = {8, 7, 7, 6, 6} – 5 листьев в кроне дерева, лучший помечен как F=6. Эту ветку и имеет смысл продолжать развивать дальше, как самую (пока) перспективную. Опускаемся в дереве на ярус ниже (Н=2), порождая новые вершины из вершины 3 … .
Ход 2 (H = 2).
Этот ход дает нам всего два варианта. (Вариант хода «фишка 5 вправо» возвращает нас к ранее рассмотренному ходу и не оценивается).
| 2 | 4 | |
| 1 | 5 | 3 |
| 7 | 8 | 6 |
Фишка «3» идет вниз. На своем месте 3 фишки «5, 7, 8». То есть не на своем месте стоит 6 фишек из девяти. G=6. H=2. F = G + H = 8
| 2 | 4 | 3 |
| 1 | 5 | 6 |
| 7 | 8 |
Фишка «6» идет вверх. На своем месте 5 фишек «3, 5, 6, 7, 8, пусто». То есть не на своем месте стоит 3 фишки из девяти. G=3. H=2. F = G + H = 5
Лучшей вершиной из рассмотренных является именно последняя вершина (F=5). В дереве она помечается как вершина N=4 (полученная четвертой).
|
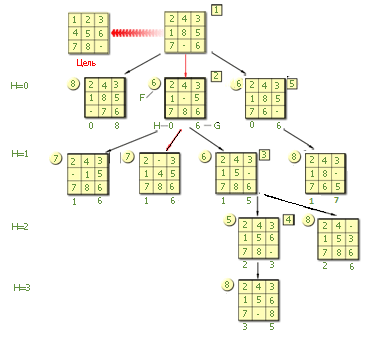
Ход 3 (H = 3).
Этот ход дает нам один вариант. (Вариант хода «фишка 6 вниз» возвращает нас к ранее рассмотренному ходу и не оценивается).
| 2 | 4 | 3 |
| 1 | 5 | 6 |
| 7 | 8 |
Фишка «8» идет вправо. На своем месте 4 фишки «3, 5, 6, 7». То есть не на своем месте стоит 5 фишек из девяти. G=5. H=3.. F = G + H = 8
|
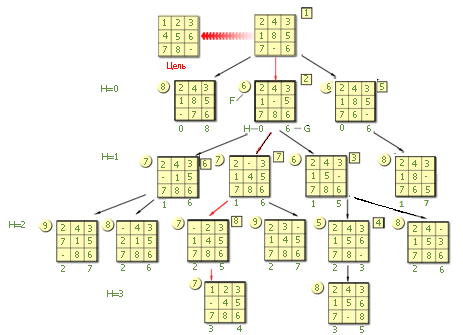
В рассмотренном к настоящему времени дереве имеется 9 вершин (плюс один корень), листьев из них - 6. Их оценки (обходя дерево слева направо): 8, 6, 6, 7, 7, 6, 5, 8, 8.
Если обходить крону дерева (листья) – вершины с оценками 8,7,7,8,8,6, то самая перспективная для рассмотрения сейчас вершина с оценкой 6 в ярусе Н=0.
| 2 | 4 | 3 |
| 1 | 8 | 5 |
| 7 | 6 |
Ход 1 (H = 1).
Из нее возможен один переход – фишка «5» идет вниз.
| 2 | 4 | 3 |
| 1 | 8 | |
| 7 | 6 | 5 |
Оценка состояния: G=7, H=1, F=8.
Дерево теперь имеет вид.
|
Так как вершина, которая только что порождена имеет значение F больше, чем значения F у имеющихся в кроне вершин, то перейдем к более перспективным вершинам из ряда (8, 7, 7, 8, 8, 8).
Следующей перспективной вершиной #6 будет вершина с первой из оценок 7.
Среди вершин в дереве с подобной оценкой, возьмем первую, встретившуюся по его обходу сверху вниз и слева направо (называется «правило северо-западного угла»).
| 2 | 4 | 3 |
| 1 | 5 | |
| 7 | 8 | 6 |
В дереве она помечается как вершина N=6 (полученная шестой).
Ход 2 (H = 2).
Из данной позиции возможно только два варианта хода.
| 4 | 3 | |
| 2 | 1 | 5 |
| 7 | 8 | 6 |
Фишка «2» идет вниз. На своем месте 3 фишки «3, 7, 8». То есть не на своем месте стоит 6 фишек из девяти. G=6. H=2. F = G + H = 8
| 2 | 4 | 3 |
| 7 | 1 | 5 |
| 8 | 6 |
Фишка «7» идет вверх. На своем месте 2 фишки «3, 8». То есть не на своем месте стоит 7 фишек из девяти. G=7. H=2. F = G + H = 9
|
Рассмотрение данной ветки пока прерывается, так как среди вершин дерева имеются вершины с лучшими оценками, чем полученные только что. Пока лучшей оценкой (7) обладает вершина из яруса 1.
| 2 | 3 | |
| 1 | 4 | 5 |
| 7 | 8 | 6 |
В дереве она помечается как вершина N=7 (полученная седьмой).
Из данной вершины можно сделать только два варианта хода. (Ход «фишка 4 вверх» повторяет уже рассмотренный ранее ход и не рассматривается).
Ход 2 (H = 2).
| 2 | 3 | |
| 1 | 4 | 5 |
| 7 | 8 | 6 |
Фишка «2» идет вправо. На своем месте 4 фишки «2, 3, 7, 8». То есть не на своем месте стоит 5 фишек из девяти. G=5. H=2. F = G + H = 7
| 2 | 3 | |
| 1 | 4 | 5 |
| 7 | 8 | 6 |
Фишка «3» идет влево. На своем месте 2 фишки «7, 8». То есть не на своем месте стоит 7 фишек из девяти. G=7. H=2. F = G + H = 9
|
Сейчас самой перспективной вершиной в дереве среди листьев его кроны является только что полученная вершина с оценкой 7 из второго хода.
| 2 | 3 | |
| 1 | 4 | 5 |
| 7 | 8 | 6 |
В дереве она помечается как вершина N=8 (полученная восьмой).
Из нее возможен только один вариант хода.
Ход 3 (H = 3).
| 1 | 2 | 3 |
| 4 | 5 | |
| 7 | 8 | 6 |
Фишка «1» идет вверх. На своем месте 5 фишек «1, 2, 3, 7, 8». То есть не на своем месте стоит 4 фишки из девяти. G=4. H=3. F = G + H = 7
В дереве она помечается как вершина N=9 (полученная девятой).
|
Это вершина с лучшей к данному моменту оценкой, равной 7. Поэтому пока следует рассматривать ее.
Из данной вершины есть два варианта хода.
Ход 4 (H = 4).
| 1 | 2 | 3 |
| 4 | 5 | |
| 7 | 8 | 6 |
Фишка «4» идет влево. На своем месте стоят 6 фишек «1, 2, 3, 4, 7, 8». То есть не на своем месте стоит 3 фишки из девяти. G=3. H=4. F = G + H = 7
| 1 | 2 | 3 |
| 7 | 4 | 5 |
| 8 | 6 |
Фишка «7» идет вверх. На своем месте 4 фишки «1, 2, 3, 8». То есть не на своем месте стоит 5 фишек из девяти. G=5. H=4. F = G + H = 9
|
Лучшей оценкой 7 пока в дереве обладает вершина из четвертого хода:
| 1 | 2 | 3 |
| 4 | 5 | |
| 7 | 8 | 6 |
В дереве она помечается как вершина N=10 (полученная десятой). Следующий за ходом 4 – ход 5.
Из нее возможны три варианта хода.
Ход 5 (H = 5).
| 1 | 3 | |
| 4 | 2 | 5 |
| 7 | 8 | 6 |
Фишка «2» идет вниз. На своем месте 5 фишек «1, 3, 4, 7, 8». То есть не на своем месте стоит 4 фишки из девяти. G=4. H=5. F = G + H = 9
| 1 | 2 | 3 |
| 4 | 5 | |
| 7 | 8 | 6 |
Фишка «5» идет влево. На своем месте 7 фишек «1, 2, 3, 4, 5, 7, 8». То есть не на своем месте стоит 2 фишки из девяти. G=2. H=5. F = G + H = 7
| 1 | 2 | 3 |
| 4 | 8 | 5 |
| 7 | 6 |
Фишка «8» идет вверх. На своем месте 5 фишек «1, 2, 3, 4, 7». То есть не на своем месте стоит 4 фишки из девяти. G=4. H=5. F = G + H = 9
|
Самой перспективной вершиной в дереве является вершина с оценкой 7, вторая на пятом ходе.
В дереве она помечается как вершина N=10 (полученная десятой).
| 1 | 2 | 3 |
| 4 | 5 | |
| 7 | 8 | 6 |
Из нее возможны два варианта хода. Следующий ход 6.
Ход 6 (H = 6).
| 1 | 2 | |
| 4 | 5 | 3 |
| 7 | 8 | 6 |
Фишка «3» идет вниз. На своем месте 6 фишек «1, 2, 4, 5, 7, 8». То есть не на своем месте стоит 3 фишки из девяти. G=3. H=6. F = G + H = 9
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 |
Фишка «6» идет вверх. На своем месте 9 фишек «1, 2, 3, 4, 5, 6, 7, 8, пусто». Цель достигнута.
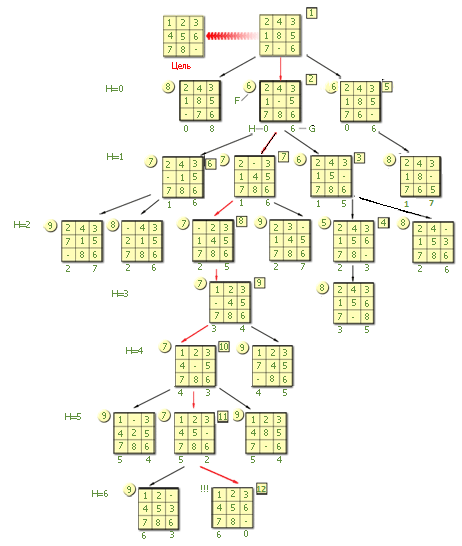
Все дерево и порядок ходов, сделанных компьютером, представлены на рисунке.
|
Обратите внимание на ярусы (помечены переменной Н), номера лучших вершин (помечены в квадрате справа вверху матрицы), оценку тактики (G – внизу и F – слева от матрицы). Красным цветом указана наилучшая (идеальная, оптимальная) траектория игры, если бы она была сразу известна.
Подведем итоги.
Статистика игры.
Всего просмотрено, считая исходную вершину, 23 вершины (это общие затраты на поиск).
В ходе игры были признаны лучшими 12 (включая исходную)..
Просматривая дерево в конце игры, выделяем в нем траекторию (показана красным цветом на рисунке), соединяющую исходную вершину с последней вершиной, в которой цель достигнута, по наикратчайшему расстоянию в дереве. Траекторию образуют вершины, помеченные как 1, 2, 7, 8, 9, 10, 11, 12. Это оптимальные вершины – лучшие среди лучших, их 8. То есть цель достигается за 7 переходов в дереве. Заметим, что эта оптимальная траектория не совпадает с траекторией поиска: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 (помечена квадратными отметками). К сожалению, найти сразу оптимальную траекторию не удается, поэтому приходится реально порождать большее дерево, чем оптимальное.
Эффективность перебора можно оценить, как 8/23 (КПД = Результат/Затраты), что составляет кпд интеллекта порядка 35%.
Примечание: очень высокий показатель, кпд паровоза, для сравнения, составляет 4-5%, и этого инженеры XX века добивались около 100 лет, начиная с 2-3%.
Интересной характеристикой является рисунок игры, представленный деревом. Ширина дерева в самом широком месте составляет 6 вершин. Глубина дерева, на которую мы заглядывали, пытаясь угадать правильное направление движения, равна 1.
Посмотрим, как меняется значение G в зависимости от номера хода вдоль траектории поиска (рисунок). Видим овраг и успешное его преодоление системой. Видно, как постепенно система минимизирует критерий G, приближаясь к решению: G=0. Хотя иногда проваливается в овраг (тупик), но успешно выходит из него, достигая цели. (Чем меньше оврагов, тем выше кпд).
Основным препятствием ИС являются овраги, основным критерием интеллектуальности – кпд. Результат ИС – построение наилучшего алгоритма достижения цели. Средство достижения результата – построение модели окружающего мира и решение (построение алгоритма) задачи на этой модели путем получения ответа на поставленный вопрос.
|
|
| Рисунок - Изменение значения критерия G во время поиска оптимальной траектории |
![[ Рис. Изменение значения критерия G во время поиска оптимальной траектории ]](lection37/img15.png "[ Рис. Изменение значения критерия G во время поиска оптимальной траектории ]")
Естественно, если тактику изменить, то статистика игры и ее кпд изменится.
Никакая тактика в общем случае не гарантирует последовательного приближения к цели из любого начального состояния, что соответствовало бы полному совпадению траектории поиска и оптимальной траектории и кпд, равному 100%.
Как видно, изменение значения критерия происходит нелинейно, а это значит, что ИС приходится сталкиваться с проблемой увязания в ходе решения задачи в «ямах», локальных экстремумах. Если ИС обнаруживает, что дальнейшее движение по ветви бесперспективно, то она пытается сменить ветку, выскочить из нее, попробовать «счастья» в другом месте. А это значит, что меняется траектория движения и, как следствие, падает кпд.
Однако во всем этом не следует видеть одни только недостатки. Конечно, никому не кажется привлекательным поиски в тупиках, но умение ориентироваться в тупиках, ямах и выходить из них – признак интеллекта. Способность пробовать и ошибаться позволяет увеличить гибкость в действиях ИС, благотворно сказывается на возможности ИС исправить ситуацию в случае неудачи. А неудачи объективны в силу сложности решаемых ИС проблем, в силу их нелинейности.
При этом следует заметить, что данная игра довольно проста. Например, игра «крестики-нолики» на матрице 3 на 3 по оценке исследователей имеет 9! = 362 880 вершин в дереве игры. С учетом симметричности ряда позиций количество вершин в дереве уменьшается до 60 000, но все равно это очень много.
Если говорить о шахматах, то просмотр на 5 ходов вперед порождает дерево игры с количеством вершин 1015. Как известно, обычно средняя игра в шахматы продолжается около 40 ходов. Просмотр вперед на 40 ходов порождает дерево с количеством вершин 10120. Для того чтобы ощутить эту величину, скажем, что с момента Большого взрыва до наших дней прошло не более 1080 секунд. Так что если некто хотел бы проанализировать такую проблему и найти оптимальную траекторию (допустим, затратив на обдумывание одного хода одну секунду), то он не успел бы этого сделать даже, если бы начал заниматься этим с момента сотворения мира. По этому поводу есть такая поговорка (мем), характеризующая комбинаторный взрыв и сложность решаемых человеком в этой связи задач:
«Бог не успел еще сыграть свою первую партию в шахматы».
Искусственный интеллект имеет дело (в отличие от других дисциплин) с бесконечностью – ищет, как и наш мозг, решение в бесконечной области. В то время как другие дисциплины идеализируют изучаемый предмет и заранее упрощают его.
Например,
- физик: «представим материальное тело в виде точки, которая не имеет размеров, но имеет ненулевую массу»,
- медик: «предположим, что у больного только одна болезнь, и мое лекарство его вылечит, не навредив другим органам»,
- математик: «предположим, что цистерна имеет вид цилиндра и к ней можно применить формулу вычисления интеграла», и так далее.
А если критерий (тактику) изменить?
При записи критерия в другом виде ход игры, вид дерева и эффективность тактики изменится.
В критерии, например, можно применять коэффициенты, усиливающие вес какой-либо части тактики. Например, критерий F=G+4*H заставляет по возможности больше внимания уделить экономии количества ходов игры, быстрее стремиться к цели. За значение H штрафуют в 4 раза больше по сравнению с G, объявляя тем самым то, что время H нам дороже, чем G. Рисунок игры при этом меняется. Теоретически дерево становится шире, поскольку проходы вниз лимитируются. ИС исследует область допустимых решений после каждого хода более тщательно, рассматривая все короткие продолжения. При этом ИС напоминает игрой человека (назовем его ‘консерватор’), который долго не решается сделать ход, тщательно просматривая все ближайшие варианты. При этом у него не остается времени на глубокий просмотр последствий своих решений. Теоретически это приводит к тому, что траектория поиска вынуждена стать скачкообразной, чаще сменяются ветки, так как они весьма необоснованно выбраны. КПД такой игры падает.
Другой критерий F=4*G+H меняет роли частей тактик. Теперь в дереве появляются длинные ветви - плети. Система исследует кинжальными проходами продолжения игры на несколько ходов вперед. Игра ИС начинает приобретать авантюрный характер, увлекающийся отдельными идеями, каждая из которых просматривается достаточно подробно и далеко. КПД такой игры из-за этого тоже может оказаться маленьким.
Используя аналогию с игрой человека определенного склада ума и характера, весовые коэффициенты k1 и k2 критерия F=k1*G+k2*H в тактике можно назвать коэффициентами темперамента (КТ): «авантюрный – консервативный» (часто в литературе их сравнивают с «мужским – женским» или «развивающим - сохраняющим», «активным – пассивным»).
|
В принципе это один коэффициент K: F=G+k2/k1*H->min или F=G+k*H->min.
Если сравнивать результат игр при различных значениях k, то эффективность тактик будет различна. Какая из тактик будет более эффективна, могут показать эксперименты, во время которых будут меняться k и одновременно измеряться эффективность игры. Конечно, для точности надо играть несколько игр с одним набором значений КТ и разными начальными условиями, усредняя значения эффективности.
Во всяком случае, ИС, которая может подбирать наилучшие КТ, анализируя таблицу эффективности, может считаться более интеллектуальной, чем та, которая этого не может делать. В этом случае Боги делегируют часть своих интеллектуальных возможностей ИС.
Примечание: забегая вперед, могу сказать, что лучшее значение коэффициента темперамента k (то есть кем лучше быть – авантюристом или консерватором, мужчиной или женщиной) различно и зависит от свойств среды, правил игры и т.п.
Например, при многократном проигрывании игры возможна автоматическая подстройка коэффициентов темперамента (второй уровень интеллектуальности).
Если при увеличении (уменьшении) какого-либо коэффициента в критерии в двух подряд играх наблюдается улучшение критерия, то полезно продолжать изменять коэффициент в том же направлении, иначе следует развернуться и пойти в обратную сторону, иногда с уменьшенным размером шага изменения искомого коэффициента (дихотомический поиск). Такой прием реализует обучение ИС в процессе игры.
Примечание: в наших лекциях по «Моделированию систем» вопрос поиска экстремума (или корней) функции (модели) уже обсуждался по адресу: http://www.stratum.ac.ru/education/textbooks/modelir/lection20.html
Ниже на рисунке можно увидеть, как меняется критерий F в зависимости от величины коэффициента темперамента k в игре «Восьмяшки» (усреднение по 10-кратным запускам игры из случайных начальных условий при заданном значении k).
|
|
| Рисунок – Зависимость критерия F от значения весового коэффициента темперамента k |
![[ Рис. Зависимость критерия F от значения весового коэффициента темперамента k ]](lection37/img17.png "[ Рис. Зависимость критерия F от значения весового коэффициента темперамента k ]")
Можно ли сделать систему еще более интеллектуальной? Все-таки мы, Боги, за нее придумали критерий, и это, благодаря ему, ИС выиграла. Было бы хорошо, чтобы ИС сама «придумывала» тактику. Организовать такое возможно.
На третьем уровне достаточно выдать ИС список концептов {H, G, …} и список операций {+, -, *, /, ^, …}.
ИС может случайным образом выбирать концепты и соединять их между собой операциями тоже случайным образом, пробуя тот или иной вариант.
Для этого можно использовать генератор случайных чисел, равномерно распределенных в интервале [0,1]. Далее надо разбить интервал [0,1] на равные части по количеству концептов (каждый концепт закрепляется за определенной частью интервала [0,1]) и определить, в какую часть попадет сгенерированное ГСЧ случайное число. Соответствующий концепт надо поставить на текущее знакоместо в выражении тактики. Также поступают и со знаками операций.
|
|
| Рисунок – Метод генерации критерия с помощью генератора случайных чисел |
![[ Рис. Метод генерации критерия с помощью генератора случайных чисел ]](lection37/img18.png "[ Рис. Метод генерации критерия с помощью генератора случайных чисел ]")
Разумеется, среди сгенерированных таким образом тактик будут как плохие, так и хорошие. Какие из них следует отобрать, покажет эксперимент.
Обращаясь из ИС третьего уровня к ИС второго уровня, которая подбирает наилучшие для тактики численные значения коэффициента темперамента, можно фиксировать эффективность, которую показывает каждая тактика за серию игр.
Разумеется, перебирать подряд все возможные комбинации не желательно, поэтому следует применить одну из универсальных процедур целенаправленного поиска, отбирающую лучшие тактики и улучшающую их по мере перебора. Подобные процедуры изучаются в курсе «Исследования операций». В курсе «Искусственного интеллекта» этой цели служат генетические алгоритмы с построением дерева эволюции тактик (моделей мира).
ИС третьего уровня, «придумывающая» тактики, более интеллектуальна, чем ИС второго уровня.
ИС четвертого уровня сама создает списки концептов и операций с помощью процедур их синтеза из более простых понятий, поручая остальное ИС более низких уровней. Очевидно, с ростом уровня ИС становится все более интеллектуальной, как мы ранее и говорили. ИС является существенно иерархической.
Итоги дня.
Сегодня мы не построили модель автоматически.
Модель – правило, оценочная функция. Найденная оптимальная траектория от исходного состояния к целевому – решение задачи с использованием модели, ответ на вопрос.
Модель была предложена человеком. Компьютер выполнил моделирование, проинтерпретировал модель, решил задачу. Однако мы обсудили, как модель можно было бы построить автоматизированным способом. Интереснее было бы, чтобы компьютер сам построил такую модель, а потом воспользовался ею для поиска решения.
Домашнее задание по практике 1
Напишите программу, умеющую играть в одну из игр (по Вашему выбору – пятнашки, крестики-нолики, футбол, ним, кант, шахматы, шашки, го и тому подобное другое).
Задайте начальное состояние игры.
Постройте дерево игры, выделите оптимальную траекторию, проанализируйте его, сняв статистику.
Обратите внимание.
При изменении вида критерия ход игры, вид дерева и эффективность тактики изменится.
В критерии можно применять коэффициенты, усиливающие вес какой-либо части тактики. Например, критерий F=G+10*H заставляет по возможности больше внимания уделить экономии числа ходов игры, быстрее стремиться к цели.
Тактика в общем случае не гарантирует последовательного приближения к цели. Возможно увязание в ходе решения задачи в «ямах». Для выскакивания из ям применяют увеличение шага игры, подмешивание случайных чисел в критерий.
Цель достижима не из любой начальной комбинации.
При многократном проигрывании игры возможна автоматическая подстройка коэффициентов критерия. Если при увеличении (уменьшении) какого-либо коэффициента в критерии в двух подряд играх наблюдается улучшение критерия, то полезно продолжать изменять коэффициент в том же направлении, иначе вернуть его обратно к старому значению. Это так называемый режим дообучения тактики в процессе игры.
В играх с противоречивыми интересами рекомендуется при расчете ходов применять минимаксную стратегию [1, 85-96].
Написание программы с уровнем интеллектуальности 2, 3 и более оценивается дополнительными баллами.
При сдаче программы демонстрируется ее работа в двух режимах: обучение и принятие решений (прогноз новых данных).
Пример ручного задания:
Начальное состояние
| 2 | 1 | 6 |
| 4 | - | 8 |
| 7 | 5 | 3 |
Целевое состояние
| 1 | 2 | 3 |
| 8 | - | 4 |
| 7 | 6 | 5 |
![[ ]](img/themes/prev1.gif "[ ]"){kind=small} |
О руководителе курса «Моделирование систем» | Лекция 02. Линейные регрессионные модели | ![[ ]](img/themes/next1.gif "[ ]"){kind=small} |
||||||||||||||
|
|||||||||||||||||