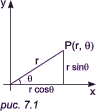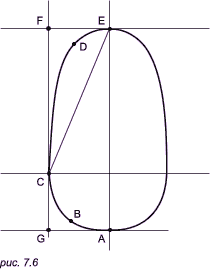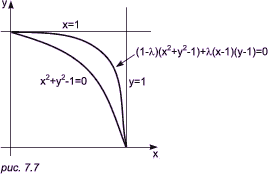Некоторые вопросы аналитической геометрии на плоскости

Рассмотрим несколько общеупотребительных методов, чтобы на их примере показать широкое разнообразие приемов, которые можно успешно использовать для решения различных задач.

Использование полярных координат для кривых с осевой симметрией

Для описания различных фигур на плоскости, образованных замкнутыми кривыми линиями, которым отчасти присуща осевая симметрия, довольно часто используется система полярных координат, показанная на рис. 7.1, в которой координаты точки P задаются радиусом r = OP и углом q = ХОР.

Полярные координаты и декартовы координаты связаны соотношениями:
x = r * cosq,
y = r * sinq.

Уравнение кривой в полярных координатах связывает r и q. Если уравнение в полярных координатах имеет явный вид r = r(q), то уравнения
x = r(q) * cosq,
y = r(q) * sinq
суть параметрические уравнения этой кривой.

Уравнения вида
r = a + b * cosnq,
представляющие замкнутую кривую с n выступами, симметрично расположенными по окружности (рис. 7.2) позволяют описывать в полярных координатах различные профили. Кривые такого вида применяются не только для простых кулачков; на их основе можно проектировать поперечные сечения тел, у которых коэффициенты a и b меняются вдоль оси, перпендикулярной плоскости Оxy.

Полярные координаты имеют целый ряд недостатков:

• отсутствие простой связи между системами полярных координат с различными точками отсчета;
• описание касательных и нормалей в полярных координатах осуществляется непросто, поэтому касательные и нормали следует определять при помощи параметрических уравнений в декартовых координатах;
• полярный угол q точки Р (x, y) находится только при помощи обратных тригонометрических функций.

Определение конических сечений, удовлетворяющих заданным условиям непрерывности и касания

Лайминг (1944) дал применение классических методов теории конических сечений к вопросу проектирования поперечных сечений фюзеляжа самолета. Его метод основан на использовании сегментов конических сечений, удовлетворяющих условиям сопряжения и, возможно, касания в нескольких точках.

Коническое сечение общего вида описывается уравнением второго порядка ax² + 2hxy + by² + 2gx + 2fy + c = 0, причем вид этого сечения определяется коэффициентами a, b, c, f, g и h. Для нахождения a, b, c, f, g и h можно было бы в принципе наложить пять независимых условий и решить соответствующие уравнения для отношений этих коэффициентов к одному из них. 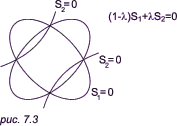Так, если кривая проходит через точку (x₁, y₁), коэффициенты удовлетворяют уравнению
ax²₁ + 2hx₁y₁ + by²₁ + 2gx₁ + 2fy₁ + c = 0,
и если касательная в точке (x₁, y₁) образует с осью Ox угол q₁, то
(ax₁ + hy₁ + g)cosq₁ + (hx₁ + by₁ + f)sinq₁ = 0.

Наложив пять независимых условий подобного рода, мы получаем систему из пяти линейных уравнений для отношений a:b:c:f:g:h. Чтобы избавиться от необходимости решения этих уравнений, Лайминг пользуется следующими известными классическими приемами, демонстрирующими некоторые преимущества уравнений неявного вида.

Прежде всего заметим, что если два конических сечения задаются уравнениями S₁(x, y) = 0 и S₂(x, y) = 0 (или для краткости S₁ = 0 и S₂ = 0), то уравнение (1 - l)S₁ + lS₂ = 0 (*) удовлетворяется как для точек, принадлежащих S₁ = 0, так и для точек S₂ = 0. Уравнение (*) в этом случае (поскольку оно второго порядка) определяет еще одно коническое сечение, проходящее через точки пересечения кривых S₁ = 0 и S₂ = 0, при любых значениях l (рис. 7.3). При варьировании величины l образуется семейство (или пучок) конических сечений, два из которых определяются уравнениями S₁ = 0 (при l = 0) и S₂ = 0 (при l = 1).

Для определения величины параметра l в общем случае необходимо задать еще одну точку (которая не является точкой пересечения), лежащую на кривой (1 - l)S₁ + lS₂ = 0. Если этой точкой является точка P₁(x₁, y₁), то
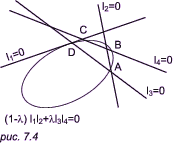
l = S₁(x₁, y₁)/(S₁(x₁, y₁) - S₂(x₂, y₂)).

Заметим далее, что уравнение (a₁x + b₁y + c₁)(a₂x + b₂y + c₂) = 0, или l₁l₂ = 0, является уравнением второго порядка, которому удовлетворяют все точки, лежащие на паре прямых l₁ = 0 и l₂ = 0. Это уравнение фактически определяет вырожденное коническое сечение, получаемое в результате рассечения конуса плоскостью, проходящей через его вершину параллельно оси. Такую пару прямых можно использовать для определения невырожденных конических сечений при помощи уравнения (*).

Итак, мы видим, что уравнение (1 - l) * l₁ * l₂ + l * l₃ * l₄ = 0 представляет семейство, или «пучок» конических сечений, проходящих через четыре точки пересечения двух пар прямых линий (l₁, l₂) и (l₃, l₄) (см. рис. 7.4). Задавая произвольную пятую точку, можно определить значение l (cм. пример 2 в конце этого раздела).

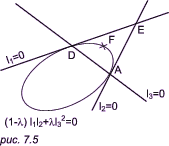
Используя этот метод, можно найти коническое сечение, имеющее две заданные касательные в двух точках и проходящее через третью заданную точку. Из рис. 7.4 видно, что по мере продвижения точки C к точке D хорда CD стремится к касательной (в точке D) к изображенному на рисунке коническому сечению. Подобным же образом, если B сдвигается к A, хорда AB стремится к касательной к этому сечению в точке A. Следовательно, если прямые l₃ = 0 и l₄ = 0 совпадают, то уравнение (1 - l) * l₁ * l₂ + l * l²₃ = 0 представляет пучок конических сечений, проходящих через точки A и D, причем l₁ является касательной в точке A, а l₂ — касательной в точке D (рис. 7.5). Выбор третьей точки F определяет параметр l.

Коническое сечение в данном случае определяется четырьмя точками: двумя точками касания A и D, точкой пересечения касательных E и некоторой четвертой точкой F, так называемой опорной точкой. Если F выбрана внутри треугольника AED, коническое сечение всегда образует непрерывную кривую между точками A и D, проходящую внутри треугольника AED. Если F делит пополам прямую, соединяющую середины отрезков DE и AE, то коническое сечение является параболой, известной под названием пропорциональной кривой. Если F находится между этой параболой и прямой AD, то мы получаем эллипс. Если же эта точка находится за пределами параболы, то мы получаем гиперболу.

В предложенном Лаймингом методе проектирования поперечного сечения фюзеляжа самолета конфигурация каждого сечения определяется пятью точками (рис. 7.6).

Поскольку каждое сечение симметрично относительно вертикальной оси, мы должны проектировать только половину сечения, причем касательные в точках E и A должны быть горизонтальными прямыми. Поскольку точка C является точкой максимальной ширины сечения, касательная в C должна иметь вертикальное направление. Проектируемое сечение состоит из двух конических сечений с общей касательной в точке C. Фюзеляж в целом описывается пятью кривыми-следами точек A, B, C, D и E, которые эти точки оставляют при движении плоскости поперечного сечения вдоль оси z.

Пример 1. Применяя метод Лайминга, можно обеспечить гладкий переход от кругового к квадратному поперечному сечению, лежащему в другой плоскости.

Пусть круговое сечение задается уравнением x² + y² - 1 = 0, а квадратное сечение — парой прямых линий x = 1, y = 1 (рис. 7.7). Тогда конические сечения
(1 - l)(x² + y² - 1) + l(x - 1)(y - 1) = 0,
где l принимает значения между 0 и 1, дают гладкий переход между двумя заданными сечениями.

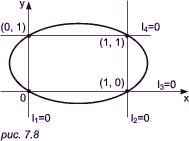
Пример 2. Найдем коническое сечение, проходящее через точки (0, 0), (1, 0), (1,1), (0, 1) и (3/2, 1/2).

Прежде всего нужно найти две такие пары прямых линий, для которых первые четыре заданные точки будут точками их пересечения. В наиболее простом случае такими парами будут l₁ = x = 0, l₂ = x - 1 = 0 и l₃ = y = 0, l₄ = y - 1 = 0, что и показано на рис. 7.8. Следовательно, любое коническое сечение, проходящее через эти точки, описывается уравнением (1 - l) * x(x - 1) + ly(y - 1) = 0 для некоторого значения l. Поскольку пятая точка имеет координаты (3/2, 1/2), то
(1 - l) * 3/2 * 1/2 + l * 1/2 * (-1/2) = 0,
откуда l = 3/4. Таким образом, x(x - 1)/4 + 3y(y - 1)/4 = 0.

Следовательно, x² + 3y² - x - Зy = 0 является уравнением искомого конического сечения (в данном случае эллипса).

Огибающая семейства кривых

При проектировании движущихся деталей станков, а также при определении свободного пространства, необходимого для движения деталей, довольно часто нужно бывает установить границу области, покрываемой контурами деталей во всех положениях в процессе их движения (рис. 7.9). Искомая граничная кривая называется огибающей семейства кривых и вычисляется следующим образом.

Если кривая, ограничивающая движущуюся деталь в момент t, имеет уравнение f(x, y, t) = 0, то каждая точка искомой граничной кривой должна удовлетворять этому уравнению при некотором значении t. Точка пересечения двух кривых f(x, y, t) и f(x, y, t + dt) = 0 при малом dt расположена близко от граничной кривой. В этой точке f(x, y, t + dt) - f(x, y, t)/dt = 0, поскольку оба члена в числителе равны нулю. Следовательно, рассматриваемая точка огибающей удовлетворяет этому уравнению в пределе при dt -> 0. 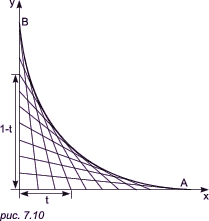Чтобы найти огибающую, мы должны решить систему уравнений
f(x, y, t) = 0
дf/дt(х, y, t) = 0.

Пример. Рассмотрим прямые (рис. 7.10), определяемые уравнением f(x, y, f) =tx + (1 - t)y + t(t - 1) = 0. Тогда дf/дt = x - y + 2t - 1 = 0. Исключая t, мы получаем уравнение огибающей в неявном виде:
x² - 2xy + y² - 2x - 2y + 1 = 0.

Если же исключить по отдельности сначала x, а затем y, мы получим параметрические уравнения x = (1 - t)², y = t².

(В этом примере показан классический способ построения так называемой пропорциональной кривой для частного случая прямолинейных отрезков OA и AB.)

Если же, с другой стороны, кривые семейства f(x, y, v) = 0 описываются параметрическими уравнениями x = x(u, v), y = y(u, v), где u — параметр, определяющий положение точки на любой заданной кривой, а v —параметр, определяющий кривую семейства, то f(x, y, v) = f(x(u, v), у(u, v), v) = F(u, v), откуда F(u, v) = 0. Таким образом,
дF/дu = дf/дx * дx/дu + дf/дy * дy/дu = 0
дF/дv = дf/дx * дx/дv + дf/дy * дy/дv + дf/дv = 0
для всех точек любой кривой данного семейства. Более того, для любой точки огибающей имеем соотношение дf/дv = 0, откуда
дx/дu * дf/дx + дy/дu * дf/дy = 0
дx/дv * дf/дx + дy/дv * дf/дy = 0.

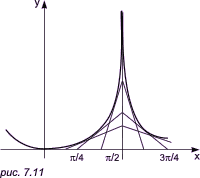
Рассматривая эти соотношения как уравнения для дf/дх и дf/дy, находим, что
дx/дu * дy/дv - дx/дv * дy/дu = 0,
если только дf/дх и дf/дy не обращаются одновременно в нуль.

Если же дf/дх = 0 и дf/дy = 0, то касательная к кривой f(x, y, v) = 0 не определена, а сама кривая должна иметь в этом случае заострение. Таким образом, чтобы получить параметрическое уравнение огибающей семейства гладких кривых, необходимо, используя (**), исключить из уравнения (*) либо u, либо v.

Пример. Рассмотрим изображенное на рис. 7.11 семейство прямых линий x = v + ucosv, y = usinv.

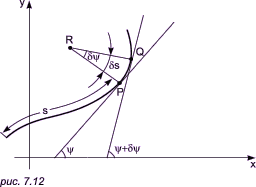
Имеем (дx/дu)(дy/дv) - (дx/дv)(дy/дu) = ucos²v - (1 - usinv)sinv = 0. Следовательно, u(cos²v + sin²v) - sinv = 0, откуда u = sinv.

Подставляя это значение u в уравнения, определяющие рассматриваемое семейство, мы получаем в конечном итоге соотношения x = v + sinv * cosv, y = sin²v, то есть параметрические уравнения огибающей (рис. 7.11).

Натуральные уравнения кривой

Если известна начальная точка кривой, то для определения этой кривой достаточно знать, как изменяется величина угла y, образованного касательной к этой кривой в некоторой точке P и осью x, в зависимости от длины s дуги данной кривой от ее начала до точки касания (рис. 7.12). Соотношение между s и y называется натуральным уравнением кривой.

Многие натуральные уравнения имеют вид s = s (y), например, уравнение цепной линии s = a * tgy. Кривизна вычисляется из натурального уравнения при помощи формулы c = dy/ds и, следовательно, в случае цепной линии, где y = arctg(s/a), мы имеем c = a/(s² + a²).

Кривая может быть задана с помощью параметрических уравнений, когда в качестве параметра берется длина дуги x = x(s) и y = y(s). Функции x(s) и y(s) связаны с y соотношениями dx/ds = cosy, dy/ds = siny.

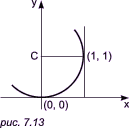
Дифференцируя эти уравнения по s и подставляя c вместо dy/ds, dx/ds вместо cosy и dy/ds вместо siny получаем систему дифференциальных уравнений
d²x/ds² + c(s)dy/ds = 0
d²y/ds² - c(s)dx/ds = 0.

Решая эти уравнения второго порядка, можно определить x(s) и y(s) для любой заданной функции кривизны c(s). Соответствующие численные методы были предложены Натбурном (1972) и Адамсом (1975). Поскольку мы свободны в выборе только четырех произвольных постоянных и длины кривой L, мы не можем задать положения и наклоны обоих концов кривой, так как для этого нужно иметь шесть условий.

Пример. В качестве простого примера вычислим изображенную на рис. 7.13 дугу окружности, используя при этом постоянство кривизны рассматриваемой кривой, и найдем аналитическое решение системы
d²x/ds² + c(s)dy/ds = 0,
d²y/ds² - c(s)dx/ds = 0.

Измеряя дугу от точки 0 и двигаясь против часовой стрелки, получим c = + 1. Поскольку c = 1, то площадь под кривой c = c(s) равна L, а поскольку изменение угла наклона равно p/2, то L = p/2. Решая теперь уравнения
d²x/ds² + dy/ds = 0
d²y/ds² - dx/ds = 0
при условиях x(0) = 0, y(0) = 0, x(p/2) = 1, y(p/2) = 1, мы получаем x = sin(s), y = 1 - cos(s), то есть, как и следовало ожидать, параметрические уравнения окружности.