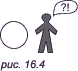Часть III / Лекция 16. Понятие размерности пространства

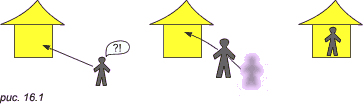
Отражение в мозгу человека окружающего реального («объективного») мира есть субъективное восприятие пространства человеком. Нарушение субъективных характеристик приводит к иллюзиям.

Объективные свойства пространства

Что такое размерность пространства и как узнать, какова размерность пространства, в котором мы живем? Чтобы выяснить это, проводились различные эксперименты. Попробуем ответить на этот и другие вопросы, воспользовавшись некоторыми анологиями и сопоставлениями.

Физический способ измерения размерности

Возьмем обыкновенный двумерный лист бумаги и начнем рисовать...

Перво-наперво, нарисуем маленького двумерного человечка, а недалеко от него — домик (рис. 16.1). Как бы человечик ни старался, он никогда не попадет внутрь своего дома: никакой предмет не сможет пройти через замкнутый контур (стенку домика), не выйдя в трехмерное пространство. Однако некий посторонний наблюдатель, находящийся в трехмерном пространстве, может поднять человечка, пронести его над стеной домика и опустить внутри него. Фактически, наш человечик ненадолго посетил трехмерное пространство!

Проведем аналогию: если какой-то предмет из нашего мира неожиданно исчез и появился совершенно в другом месте, или непостижимым образом попал внутрь замкнутого пространства (например, куба без окон-дверей), то есть основания предполагать, что предмет некоторое время находился в четырехмерном пространстве, где его и «перенесли» совсем в другое место. Если рассказы о хиллерах (людях, проводящих операции на внутренних органах человека без разрезания кожи) являются правдой, то можно предположить, что делают они это в четырехмерном пространстве. А ведь и у двумерного человечка при желании можно легко достать печень или сердце без разрезания его внешней оболочки...

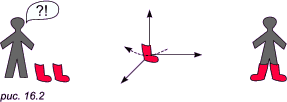
Итак, можно нарушить замкнутость контура при помощи увеличения мерности пространства.

Посмотрим теперь на рис. 16.2. Мы видим, что человечку достались два сапожка, но вот беда: оба — на левую ногу! Как бы человечик ни вращал сапожок в своем плоском пространстве, он никогда не превратит его в правый, то есть, говоря «по-научному», не сможет изменить его симметрию. Но вытащим один сапожок в трехмерное пространство, повернем его здесь на 180 градусов (фактически, изменим симметрию) и вернем обратно в плоскость листа. Теперь человечик имеет нормальную пару сапог — для правой и левой ноги. Проведем аналогию: если у нас имеется морская ракушка, закрученная по часовой стрелке, то в четырехмерном пространстве легко можно сделать так, чтобы та же самая ракушка оказалась закрученной против часовой стрелки!

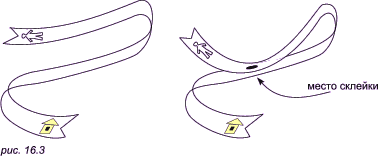
Итак, в пространстве размерности n + 1 можно менять симметрию объектов, взятых из пространства размерности n.

Превратим теперь наш воображаемый лист бумаги в длинную дорогу-полоску (рис. 16.3, слева). По этой дороге человечик должен дойти до своего дома. Очевидно, что он сможет это сделать только одним-единственным способом — честно пройдя весь заданный путь. Но представим себе, что некоторые части дороги проходили друг от друга настолько близко, что просто-напросто склеились (рис. 16.3, справа). В этом случае человечик может значительно сократить свой путь, — главное, чтобы он смог пролезть в месте склейки.

Может быть, где-то и в нашем, трехмерном мире, имеется такая «склейка», пройдя сквозь которую, можно мгновенно очутиться в галактике, находящейся от нас на расстоянии в миллиарды световых лет?..

Посмотрите теперь на рис. 16.4. Все, кроме человечка, хорошо видят, что рядом с ним нарисована окружность. Но, оказывается, и человечик тоже точно знает, что перед ним — именно окружность. Как же он догадывается об этом? Очень просто: ему достаточно со всех сторон обойти этот объект и убедиться, что с любой стороны он одинакового размера (это важно, ведь на листе бумаги можно нарисовать произвольную (ломаную) замкнутую линию, но только окружность будет видна человечку одинаково с любой стороны).

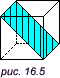
Так же и мы: в трехмерном пространстве мы не видим предмет целиком и лишь подозреваем, что он — трехмерный. Увидеть одновременно все (или хотя бы четыре) грани куба невозможно; лишь обходя его с разных сторон, мы делаем вывод, что он действительно трехмерный. Можно исхитриться и поставить позади куба зеркало, тогда три его стороны будут видны спереди, а оставшиеся три — в отражении. Однако этот трюк легко объясняется тем, что зеркало увеличивает размерность пространства на единицу. В четырехмерном пространстве можно увидеть этот же куб с четырех сторон.

Замечание 1. Система «зеркало + то, что в зеркале» представляет собой четырехмерное пространство. Замечание 2. Вообще говоря, человек все-таки может увидеть куб сразу с четырех сторон: надо просто поднести его вплотную к глазам. Но именно «к глазам»! Одним глазом мы можем видеть не более трех сторон.

Посмотрите теперь на рис. 16.5. Мы можем двухмерный объект (прямоугольник) поместить внутрь трехмерного объекта (куб). Очевидно, что площадь двумерного прямоугольника больше площади грани трехмерного куба. Таким образом, четырехмерный куб вмещает внутри себя трехмерный, а пятимерный куб — четырехмерный... Пространство с увеличением размерности n становится все более вместительным, и теоретически в некотором n-мерном пространстве можно спрятать весь наш мир...

Попробуйте теперь представить себе, как будет выглядеть четырехмерный куб! Ответ находится здесь.

Фрактальная размерность

Все мы хотя бы интуитивно представляем себе, что такое размерность, и что обычно она бывает целой. Но существует еще понятие фрактальной размерности. Оно подразумевает, что размерность может быть также и дробной.

Изобразим, к примеру, линию побережья (рис. 16.5). Возьмем линейку и будем считать, сколько линеек у нас располагается на этой линии; затем будем уменьшать шаг линейки до бесконечности: 1 м. — L₁ штук, 0.1 м. — L₂ штук, L₁ <> 10, L₂, L₁<10 L₂, Ф = L / a — фрактальная размерность. Получиться дробное число. Для прямой линии Ф стремится к 1. Для изрезанной линии Ф стремится к 2.

Математический способ измерения размерности

Чтобы отделить часть линии от остальной, достаточно двух или более точек. Но чтобы часть поверхности отделить от всей поверхности N точек недостаточно, требуется линия. Часть 3D отделяется от остального пространства поверхностью.

Размерность

1D: если каждая точка принадлежит не менее двум кусочкам (по Урысону).

2D: если каждая точка принадлежит не менее трем кусочкам (по Урысону).

3D: если каждая точка принадлежит не менее четырем кусочкам (по Урысону).

Определение Урысона: фигура имеет размерность n, если ее можно разбить на сколь угодно малые части так, чтобы ни одна ее точка не принадлежала n + 2 различным частям, но достаточно, если найдутся точки, принадлежащие n + 1 различным частям.

Физиологический способ измерения размерности

О физиологическом способе измерения размерности мы говорили на пятой лекции.

Соотношение Эйлера

Еще со школы нам хорошо известно соотношение Эйлера:
Г + В = Р + 2 или Г + В - Р = 2, где Г — число граней, В — число вершин, Р — число ребер.

В общем случае эта формула имеет вид:
N₀ - N₁ + N₂ - N₃ + ... + N_i = 1 - (-1)ⁿ, где
N₀ — количество нульмерных образов (вершин),
N₁ — количество одномерных образов (ребер),
N₂ — количество двумерных образов (граней),
...
N_i — количество i-мерных образов (гиперплоскостей или гиперграней),
n — размерность пространства.

Например, для трехмерного куба мы имеем: Г = 6, В = 8, Р = 12, то есть 6 + 8 = 12 + 2; для тетраэдра: Г = 4, В = 4, Р = 6, то есть 4 + 4 = 6 + 2.

Используя общую формулу Эйлера, можно выяснить, сколько трехмерных граней N₃ содержит в себе четырехмерный куб (n = 4). Для такого куба общая формула будет выглядеть следующим образом: N₀ - N₁ + N₂ - N₃ = 1 - (-1)⁴ = 0, откуда N₃ = N₀ - N₁ + N₂. Для четырехмерного куба число вершин N₀ = 16, число ребер N₁ = 32, число граней N₂ = 24, следовательно, число трехмерных граней N₃ = 16 - 32 + 24 = 8.