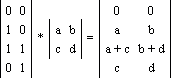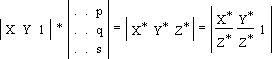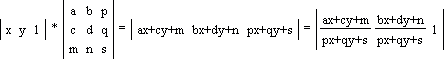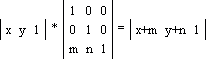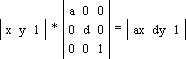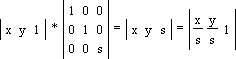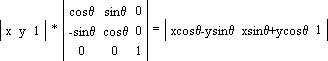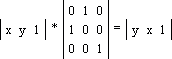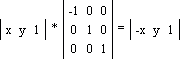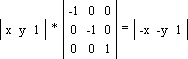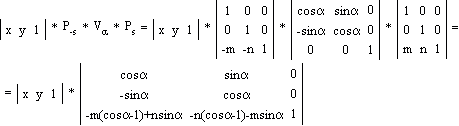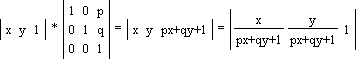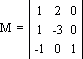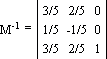Часть I / Лекция 01. Преобразования в двухмерном пространстве

Преобразования в двухмерном пространстве используются в разнообразных случаях: чтобы отдельные части объекта можно было описывать в различных координатных системах; чтобы типовые и повторяющиеся части можно было располагать в произвольных положениях на чертеже и в пространстве, в том числе с использованием циклов; чтобы без повторной кодировки можно было получать симметричные части объекта; для направленной деформации фигур, тел и их частей; для изменения масштаба чертежа, построения проекций пространственных образов... С аналитической точки зрения преобразования — это пересчет значений координат.

Преобразование точки

Точка на плоскости представляется двумя координатами: |x y|. Матрица преобразования точки выглядит так:

Ниже показано преобразование точки через квадратную матрицу; здесь x_n = xa + yc и y_n = xb + yd — новые координаты точки после преобразования:

Преобразование фигуры

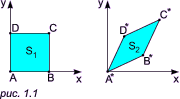
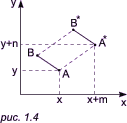
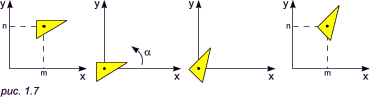
Если представить фигуру как совокупность точек, то можно провести и ее преобразование. В следующем примере задано четыре точки: A(0, 0), B(1, 0), C(1, 1), D(0, 1), каждая из которых после преобразования переходит соответственно в A^*(0, 0), B^*(a, b), C^*(a + c, b + d), D^*(c, d):

Геометрически это соответствует деформации фигуры:

При этом площадь новой фигуры равна площади старой фигуры, умноженной на детерминант матрицы преобразования: S₂ = S₁ * |ad - bc|.

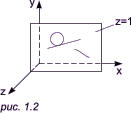
Однородные координаты. Операции в них

Любая система координат, в которой представление точки в двухмерном (трехмерном) пространстве задается при помощи трех (четырех) координат (Р₁, Р₂, Р₃(, Р₄)), называется системой однородных координат. Вообще, для n-мерного пространства число однородных координат должно быть на единицу больше: n + 1.

Применение однородных координат в общем случае позволяет устранять аномалии, возникающие при работе в декартовых координатах, и представлять сложные преобразования в виде произведения нескольких матриц.

Геометрическая интерпретация на случай двухмерного пространства: введение третьей координаты, равной единице, можно трактовать как переход в трехмерное пространство, в котором разрешено работать только в плоскости z = 1. Следует представлять себе, что экран компьютера (картинная плоскость, плоскость изображения) находится в плоскости z = 1:

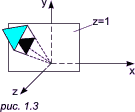
В случае выхода рисунка за сечение z = 1 рисунок возвращается принудительно в данное сечение — для того, чтобы были возможны последующие операции:

Такая операция называется нормализацией однородных координат:

Общий вид преобразования

Операция смещения

Матрица преобразования содержит в себе константы m и n, под действием которых точка смещается на m единиц вдоль оси x и на n единиц — вдоль оси y:

Операция масштабирования

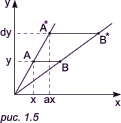
За счет коэффициентов a и d матрицы преобразования происходит увеличение (или уменьшение) значения координат точки (x, y) в a и d раз по осям x и y соответственно:

Общее полное масштабирование

В данном случае при s < 1 будет происходить увеличение значения координат точки (x, y) в s раз; при s > 1 мы получим обратный эффект — уменьшение значения координат (x, y) в s раз.

Поворот на угол q

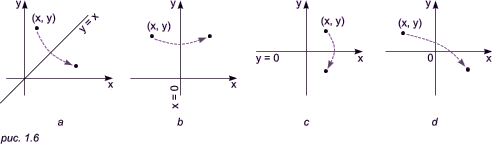
Здесь q — угол, на который требуется повернуть точку (x, y). Обратите внимание: поворот происходит относительно точки (0, 0) декартовой системы координат против часовой стрелки!

А теперь вот вам маленькое задание. Попробуйте повернуть треугольник на угол q = 90^o, координаты точек можете взять любые. Наш вариант представлен здесь.

Отображение или зеркалирование

• Зеркалирование относительно прямой y = x (рис. 1.6a):
  
• Зеркалирование относительно прямой x = 0 (рис. 1.6b):
  
• Зеркалирование относительно прямой y = 0 (рис. 1.6c):
  
• Зеркалирование относительно начала координат (рис. 1.6d):
  

Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол a

Чтобы провести любое сложное преобразование, необходимо разложить его на базовые операции. Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол a состоит из трех базовых операций: 1) перенос фигуры на вектор A(-m, -n) для совмещения точки (m, n) с началом координат; 2) поворот фигуры на угол a; 3) перенос фигуры на вектор A'(m, n) для возвращения ее в исходное положение. Так как фигуру можно представить набором точек, то операции 1) - 3) можно выполнять последовательно для каждой точки. Покажем это на примере.

Пусть мы хотим повернуть треугольник с координатами A(x, y), B(x₁, y₁), C(x₂, y₂) вокруг точки D(m, n) на угол a. Пусть P_-s — матрица переноса точки на вектор A(-m, -n), V_a — матрица поворота на угол a, P_s — матрица переноса точки на вектор A'(m, n).

Итак, мы имеем все данные, необходимые для проведения сложного преобразования первой точки A(x, y):

Точно такие же преобразования необходимо провести для оставшихся двух точек треугольника, подставляя соответствующие их координаты взамен x и y (последовательность операций см. на рис. 1.7). Таким образом, сложная операция разбивается на простейшие и задается произведением соответствующих матриц преобразования, причем порядок, в котором перемножаются матрицы, существенно определяет результат.

Центральное проецирование (перспектива)

px + qy + 1 = H — плоскость.

Примечания

1. В общем случае от перемены матриц местами результат меняется.

2. Матрицы операций, идущие подряд, можно перемножать раздельно, главное — не менять их порядок следования (см. примечание 1).

3. Линии при описанных выше (аффинных) преобразованиях переходят в линии. Поэтому обычно производится пересчет только координат вершин фигуры, а после этого соответствующие вершины в результирующей фигуре соединяются, как и в исходной фигуре.

Нахождение точки пересечения двух линий (пример)

Пусть имеются две линии: x + y = 1, 2x - 3y = 0, необходимо найти точку их пересечения. Решение может быть найдено с использованием матриц. Перенесем все члены уравнений в левую часть: x + y - 1 = 0, 2x - 3y - 0 = 0; запишем коэффициенты первого уравнения в первый столбец матрицы, второго уравнения — во второй:

Условие, при котором пересекаются две прямые, выглядит следующим образом:
|x y 1| * M = |0 0 1|

Для нахождения ответа необходимо обе части предыдущего уравнения домножить справа на обратную матрицу M^-1 (при перемножении M и M^-1 получается единичная матрица E):
|x y 1| * E = |0 0 1| * M^-1

|x y 1| = |3/5 2/5 1|

Ответ: точка пересечения прямых: x = 3/5, y = 2/5.