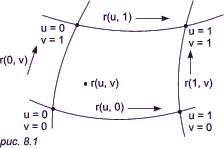
Составные поверхности. Введение: порции поверхности по Кунсу

Oбсудим ряд методов определения поверхностей. Hекоторые из этих методов основаны на системе построения двух пересекающихся семейств кривых, поэтому начнем с рассмотрения процедур этого типа. Допустим, что необходимая сетка кривых уже построена каким-либо методом. Для большей общности будем сначала применять параметрическое представление, введя семейства продольных и трансверсальных кривых; параметры этих кривых обозначим через x и y соответственно. Потом полученные результаты будут применены и к непараметрическому случаю.

Сетка кривых делит поверхность на совокупность топологически прямоугольных порций, каждая из которых ограничена парой u-кривых и парой v-кривых, как показано на рис. 8.1. Допустим, что u и v изменяются в пределах от 0 до 1 вдоль соответствующих границ; тогда r(u, v), 0 < u, v < 1, представляет внутренность порции поверхности, r(u, 0), r(1, v), r(u, 1) и r(0, v) представляют четыре известные граничные кривые. Тем самым задача определения порции поверхности сводится к нахождению функции r(u, v) с подходящим типом «хорошего поведения», которая при u = 0, u = 1, v = 0 или v = 1 представляет нужную граничную кривую.

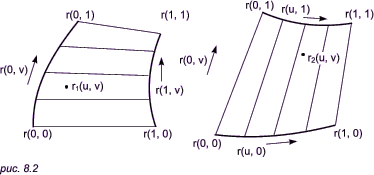
Рассмотрим сперва более простую задачу построения порции поверхности, если заданы только две ее границы r(0, v) и r(1, v). Применяя линейную интерполяцию в u-направлении, получим линейчатую поверхность
r₁(u, v) = (1 - u)r(0, v) + ur(1, v) (*).

Напротив, линейная интерполяция в v-направлении дает поверхность, удовлетворяющую двум другим граничным условиям:
r₂(u, v) = (1 - v)r(u, 0) - vr(u, 1) (**).

Эти две поверхности показаны на рис. 8.2.

Их сумма r₁ + r₂ представляет порцию поверхности, каждая из границ которой является суммой заданной граничной кривой и прямолинейного отрезка, соединяющего концевые точки этой кривой. Например, легко проверить с помощью (*) и (**), что граница, соответствующая v = 0, определяется не вектор-функцией r(u, 0), а выражением
r(u, 0) + [(1 — u)r(0, 0) + ur(1, 0)].

Тогда если мы можем найти порцию поверхности r₃(u, v), границами которой служат вышеупомянутые прямолинейные отрезки, то можно восстановить первоначальные граничные кривые, составив выражение r₁ + r₂ - r₃. Построить r₃ легко; ее границы, отвечающие v = 0 и u = 0, будут даваться выражениями
(1 - u)r(0, 0) + ur(1, 0)
(1 - u)r(0, 1) + ur(1, 1)
соответственно, и последующая линейная интерполяция в v-направлении даст
r₃(u, v) = (1 - u)(1 - v)r(0, 0) + u(1 - v)r(1, 0) + (1 - u)vr(0, 1) + uvr(1, 1) (***).

Вектор r = r₁ + r₂ - r₃, полученный из (*), (**) и (***) и определяющий искомую поверхность, удобно представить в матричном виде:

Последовательные подстановки u = 0, u = 1, v = 0 и v = 1 без труда подтверждают, что порция поверхности, определенная вектором r(u, v), имеет четыре первоначальные кривые своими границами.

Эта конструкция, использующая только информацию о границах поверхности и некоторые вспомогательные скалярные функции переменных u и v, определяет наиболее простой класс поверхностей, первоначально изученный Кунсом (1967), которые с тех пор известны как поверхности Кунса. Данная здесь трактовка принадлежит Форресту (1972). Вспомогательные функции u, (1 - u), v и (1 - v) называются функциями смешения, так как они соединяют воедино четыре отдельные граничные кривые, чтобы дать одну корректно определенную поверхность.