Математическое влияние объектов

Аддитивное влияние

Линия движется, постепенно изменяясь, превращается в другую линию, затем в третью... Это может быть движение тела змеи или изменение контура плода в процессе его роста. Во всех этих случаях имеются как минимум две заданные линии, и надо построить семейство «промежуточных», которое моделировало бы «постепенное превращение». Простейший способ построения таких кривых называется «морфингом».

Наметим на обеих исходных линиях одинаковое количество точек. Пусть это заданные в исходных координатных моделях опорные точки либо вновь построенные точки на линиях. В последнем случае их можно найти, разделив обе линии на одинаковое число равных частей.

Теперь точки с одинаковыми номерами соединяем отрезками. Вводим параметр t, соответствующий времени или фазам превращения линии. Пусть для первой исходной линии t = 0, а для второй t = 1. Для некоторой промежуточной линии зададим значение t = t_i. Теперь каждый отрезок разделим в том же отношении, в котором t_i делит интервал от 0 до 1. Координаты полученной точки на j-м отрезке можно подсчитать по простым формулам:
X_ij = X_1j(1 - t_i) + X_2jt_i
Y_ij = Y_1j(1 - t_i) + Y_2jt_i

В правой части этих формул фигурируют координаты концов отрезка. Найденные на всех отрезках таким образом точки и опишут промежуточную линию. Какие особенности имеет этот способ? Движение каждой точки линии в процессе преобразования этой линии в другую — равномерное и прямолинейное. Если обе заданные линии гладкие, то, как правило, гладкими будут и промежуточные, хотя в отдельных случаях на промежуточных линиях могут образовываться петли и особые точки. Если на исходных линиях есть изломы — на промежуточных линиях эти изломы также «отпечатываются», причем в общем случае их количество равно сумме изломов на исходных линиях. Впрочем, особым образом выбирая опорные точки на линиях, можно управлять преобразованиями так, чтобы изломы первой линии переходили в изломы второй линии.

Этот же способ используется в производстве мультфильмов. Способ можно различным образом усложнять и модифицировать. Сочетая такое преобразование с преобразованиями координат, можно получить криволинейные пути точек линии в процессе ее видоизменения. С другой стороны, исходных линий может быть не две, а несколько. Тогда вместо одного параметра t вводится несколько, и они играют роль весов, присваиваемых каждой из исходных линий. Так можно нарисовать, например, гибрид яблока, груши, банана и еще какого-нибудь фрукта.

Мультипликативное влияние

Допустим, что кривая равномерно «заряжена» в каком-то смысле, и ее «заряд» влияет на окружающее пространство, образуя некое «поле». Чем ближе к кривой, тем потенциал этого поля выше. Можно условно разбить плоскость линией на положительные и отрицательные области и принять, что потенциал с двух сторон от линии имеет разный знак. Для определения величины потенциала в точке плоскости можно подсчитать расстояние от этои точки до линии. Тогда, если задаться фиксированным значением потенциала, точки плоскости с этим значением выстроятся в эквидистанту, проведенную около линии. Но существует и другой способ построения таких линий.

Если уравнение окружности записать в неявном виде: (X - X_c)² + (Y - Y_c)² - R² = 0, и подставить в левую часть координаты какой-либо точки, не принадлежащей этой окружности, то левая часть уравнения будет равна некоторой положительной или отрицательной величине. Пусть эта величина и определяет «степень влияния». Она будет нулевой для точек самой линии и будет возрастать по мере удаления от линии. Вообще говоря, форма и математическое описание влияния зависят от того, в каком виде записано уравнение исходной кривой.

Построим линии вляния для исходной кривой особого вида. Возьмем окружность и пересекающую ее прямую (рис. 4.1). Уравнения обеих линий известны: (X - X_c)² + (Y - Y_c)² = R² и Ax + By + C = 0. После перемножения левых частей обоих уравнений мы получим следующее:
[(X - X_c)² + (Y - Y_c)² - R²][Ax + By + C] = 0.

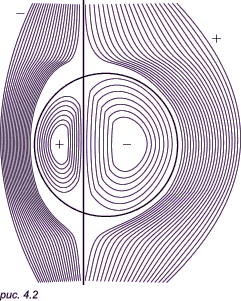
Можно произвести алгебраические преобразования и убедиться, что получилось уравнение линии третьего порядка. Тем не менее оно описывает сразу обе исходные фигуры. Теперь в правой части уравнения заменяем нуль на значение «потенциала» D и получаем уравнение «линии влияния». Перенеся параметр D в левую часть, можно получить уравнение в неявном виде, можно попытаться разрешить уравнение относительно y и затем искать корни получившегося уравнения третьей степени.

На рис. 4.2 показано семейство «линий влияния» для нашей составной фигуры. Области, на которые разделена плоскость исходными линиями, в шахматном порядке соответствуют положительным и отрицательным значениям «потенциала» (здесь однократное пересечение исходной линии соответствует изменению знака).