Практика 10. Моделирование случайных событий

Теория

Большинство систем, используемых на практике, - стохастичны. В них действуют случайные факторы, а факторов и связей настолько много, что отследить причинно-следственные связи становится невозможно. Наконец, выражения в описании таких систем настолько сложны, что решить их аналитически невозможно.

Решение инженерных задач основывается на статистическом моделировании сложных систем. На рисунке показана схема решения задач методом Монте-Карло.

Рисунок – Схема метода Монте-Карло

С помощью генератора случайных чисел вырабатывают случайные числа r надежным способом. Далее преобразуют числа r в необходимый диапазон, в котором меняются входные величины исследуемой системы. Если значения этих величин не равновероятны (стандартный ГСЧ выдает числа равномерно распределенные в [0,1]), то их приводят в соответствии с данным конкретным распределением.

Далее имитируют прохождение каждого такого сигнала через модель исследуемой системы. Естественно, на выходе модели системы появятся случайные числа. Их накапливают в счетчиках – сколько раз появилось на выходе то или иное событие. Каждый счетчик отвечает за свой тип событий: N_i. Также подсчитывается общее число экспериментов N. Далее достаточно разделить значение конкретного счетчика на число экспериментов N_i/N, чтобы узнать, как часто появляется то или иное событие в череде всех событий. Чем больше экспериментов, тем ближе это число (частота) к искомому теоретическому значению вероятности P.

Остается только построить график изменения частоты события от числа экспериментов P_i(N). Достаточно дождаться числа экспериментов, когда вероятность Р войдет в заданную трубку точности Е и сформулировать ответ. Количество экспериментов следует вести до тех пор, пока самая плохая вероятность из множества вероятностей всех типов событий войдет в трубку заданной нами точности Е.

Задача 1

А и В договорились встретиться в парке под часами с 10 до 11 часов утра. Тот, кто пришел первым, ждет второго 15 минут и уходит. Какова вероятность встречи А и В? Допустимая ошибка Е=0.1 (10%). Точность - 90%.

Решение

Выберем отрезок от 0 до 1. Будем считать 0 – отметкой «10 часов утра». 1 – отметка «11 часов утра».

Разыгрывая число r1 из интервала [0,1] с помощью ГСЧ, будем имитировать тем момент, кода приходит первый партнер. Точно также имитируем другим случайным числом r2 момент прихода второго партнера. Остается определить разницу этих чисел D=|r1-r2|. «15 минут» соответствует числу 0.25 на шкале [0,1].

Если D>0.25, то А и В не встретились. Если D<=0.25, то А и В встретились. Каждое событие отмечается в счетчике: N1 или N2.

N=N1+N2

Строим график N2/N в зависимости от N. Постепенно случайная кривая превращается в почти прямую линию.

Проведите горизонтальную линию от конца кривой. Проведите две параллельные ей линии на расстоянии ±Е от основной линии – коридор точности.

Отметьте место, где экспериментальная случайная кривая последний раз пересекла коридор точности, вошла в него и уже больше не вышла из коридора.

Это значение экспериментов N является критическим: Nкр. Удвойте и проведите число экспериментов: Nт=2*Nкр. Значение Р=N2/Nт будем считать ответом задачи.

Рисунок – График случайного процесса и трубка точности для определения количества экспериментов

Наберите в любой программной среде или математическом пакете схему задачи. Нарисуйте график и получите ответ.

Сообщите ответ другим студентам своей группы. Найдите среднее арифметическое ответов всех студентов своей группы. Ответ заведомо станет еще точнее.

Таблицу полученных чисел и их среднее приведите в тетради.

На рисунке (для понимания) показаны A реализаций (здесь, A=100) некоторого эксперимента – то, что называется ансамбль реализаций. Видны различные значения получившихся Nкр.

Рисунок – Ансамбль реализаций вероятностного эксперимента со случайными исходами и засечки их критического количества. Количество линий (реализаций) L, которые не пересекли трубку точности на момент N называется доверительной вероятностью: Q(N)=L/А

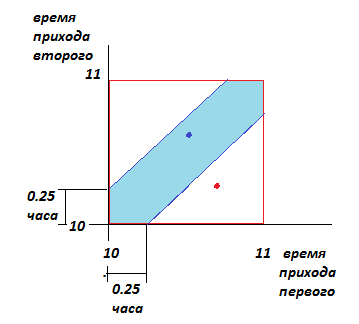
Задачу можно решить другим способом, используя геометрическое определение вероятности. На схеме показан час, предоставленный для встречи в виде квадрата, и две переменных – две оси, представляющие момент прихода партнеров. Голубая фигура указывает на область, где лежат точки с координатами r1, r2, у которых |r1-r2|<0.25. Красная точка – встреча не состоялась, синяя точка – встреча состоялась. Вероятность встречи - отношение площади голубой фигуры к красной. Найдите аналитически точное теоретическое значение вероятности. Сравните его со значением, полученным ранее по методу Монте-Карло.

Рисунок – Геометрическое решение задачи «о встрече»

Сформулируйте достоинства и недостатки аналитического метода и метода Монте-Карло.

Задача 2

Человек делает 1 раз в секунду 1 шаг от столба в сторону от него. Направление (влево-вправо) выбирается случайно. В 6 шагах от столба справа от него находится яма. Найдите методом Монте-Карло с точностью 90% время, в течение которого человек свалится в яму.

Приведите график и ответ с указанной точностью. Усредните значение в своей группе.

Приведите в тетради график, таблицу, результат

Задача 3

Найдите методом Монте-Карло вероятность того, что в группе из Х человек у двух человек (А=2) совпадает день рождения. Точность – 90%.

С помощью программы постройте график зависимости P(2, X) – Р от Х при А=2.

Измените параметр А, снимите семейство кривых Р(А, Х).

Рисунок – Зависимости распределения вероятностей от параметра задачи (результат компьютерного эксперимента)

Задача 4

Определите значение числа «пи» методом Монте-Карло до двух знаков после запятой.

Задача 5

Определите мировую константу протекания «хи» методом Монте-Карло с точностью 90%. Имеется проводящая электрический ток решетка 6 на 6, к торцам которой подведено напряжение. В цепь с решеткой и батареей последовательно включен амперметр, который фиксирует наличие тока в цепи (в решетке). Случайным образом перекусываем одно из плеч (как вертикальных, так и горизонтальных) решетки (показано крестиком).

Сколько плеч надо перекусить случайно, чтобы в цепи перестал течь ток, а решетка стала «непроводимой»?

Отношение числа выкушенный плеч к общему числу плеч называется константой протекания.

Константа была впервые определена группой английских студентов в натурном эксперименте во дворе Королевского колледжа путем разрезания сетки-рабицы для вычисления количества вводимых примесей в кристалл для получения из него полупроводника. Константа протекания используется при расчете распространения эпидемий, слухов, информации по социальным сетям, для определения доли донорских (или акцепторных) примесей в полупроводниках, производительности фильтров (например, угольных) очистки, различного рода уловителей, вероятности катастрофы спутников в околоземном пространстве, затопления земель при строительстве гидроэлектростанций, скорости заражения лесов и сельскохозяйственных угодий вредителями и так далее.

Рисунок – Схема эксперимента по определению проводимости физической решетки

Напишите алгоритм определения наличия тока в сети (решетке) и алгоритм генерации номеров для выкусывания плеч. Найдите «хи».

Усредните вычисленное значение в своей группе.