Euler's method
Динамическая система, как известно, описывается дифференциальным уравнением dx/dt=f(x,t)
или системой таких уравнений. Где x характеризует состояние системы, а f - скорость изменения этого состояния во времени. Известно также начальное (t=0) состояние системы x(0).
Чтобы рассчитать это уравнение, то есть определить поведение системы x(t), существует множество методов. В основе большей части из них лежит метод Эйлера.
Метод основан на том, что будущее определяется настоящим состоянием, к которому прибавляется изменение этого состояния за некоторое время, называемое шагом dt. Изменение состояния определяется скоростью (производной по времени) в точке исходного состояния.
БУДУЩЕЕ := НАСТОЯЩЕЕ + СКОРОСТЬ * dt
или в обозначениях, принятых в уравнении
x(t+dt) := x(t) + f(x(t),t) * dt
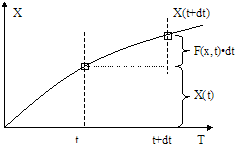
рис. 1.
Скорость по смыслу здесь производная f(x,t) и всегда может быть вычислена в точке настоящего, то есть при заданных x и t. РИС1. Рассчитав будущее на одном шаге следует переместиться в точку будущего, теперь она становится настоящим, и повторить процедуру. То есть процесс расчета носит итерационный характер - данные, полученные на одном шаге, становятся исходными для следующего шага. И так шаг за шагом.РИС2. Параллельно ведут расчет времени
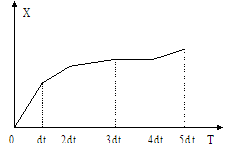
рис. 2.
t:=t+dt.
Величину dt исследователь задает произвольно как константу. Но при этом следует иметь в виду, что если выбран большой шаг расчета, то несмотря на то, что время t идет быстро, получаются менее точные результаты, так как истинная кривая заменяется за ломаную линию, образованную касательными (производными). Более того, при слишком большом шаге может возникнуть явление разболтки, когда состояние системы (значение x) резко меняет свои значения, и изменения на каждом шаге все более увеличиваются.РИС3 Реально это означает, что через несколько шагов расчет остановится, так как будет достигнуто неприемлемо большое значение для x (BigNumBigNum). Таких значений шагов следует избегать.
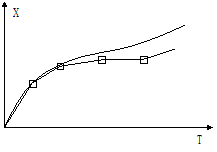
рис. 3.
Если задать малое значение шага, то расчет получится более точным, конечно, будет затрачено большее число шагов, и расчет будет идти дольше.
Следует сказать, что приемлемый размер шага определяется опытным путем. Пользователь задает размер шага в ячейке данных с именем dt в меню Свойства Имиджа | ДанныеEnvironment_options___Methods. Иногда для достижения требуемой точности приходится запускать расчет несколько раз с различными значениями dt.
Для примера покажем как идет расчет методом Эйлера для системы dx/dt=(5-x) шагом dt=0.1 от 0 до 1.Начальные условия примем x(t)=0.
|
Номер шага |
время t |
состояние x на начало шага |
скорость изменения f(x)= 5-x |
изменения за шаг x=f*dt=(5-x)*0.1 |
точное значение x |
|
0 |
0 |
0 |
5 |
0.5 |
0 |
|
1 |
0.1 |
0.5 |
4.5 |
0.45 |
0.485 |
|
2 |
0.2 |
0.95 |
4.05 |
0.405 |
0.915 |
|
3 |
0.3 |
1.355 |
3.645 |
0.365 |
1.304 |
|
4 |
0.4 |
1.720 |
3.280 |
0.328 |
1.656 |
|
5 |
0.5 |
2.048 |
2.952 |
0.295 |
1.974 |
|
6 |
0.6 |
2.343 |
2.657 |
0.266 |
2.262 |
|
7 |
0.7 |
2.609 |
2.391 |
0.239 |
2.523 |
|
8 |
0.8 |
2.848 |
2.152 |
0.215 |
2.759 |
|
9 |
0.9 |
3.063 |
1.937 |
0.194 |
2.972 |
|
10 |
1.0 |
3.257 |
- |
- |
3.165 |
Чем менее шаг в методе Эйлера, тем точнее будет решение. Метод Эйлера называют методом первого порядка, так как точность результата пропорциональна величине шага. Более точные результаты дают методы более высокого порядка (например, метод Рунге-Кутта 4 порядка). Чтобы изменить метод расчета уравнений, необходимо в меню Параметры среды | Методы | Дифференциальные уравненияEnvironment_options___Methods сменить метод выбором из списка.
Очень важно !
Вы в праве быть неудовлетворены расчетом любым методом, известно, что универсального метода не существует. Часто метод, хорошо решающий одну модель, плох для другой. Среда предоставляет автоматически только наиболее популярные методы. Но если вы решили осуществить расчет своим собственным методом, то это реализуемо.
Метод - это формулы. И в этом смысле эти формулы ничем не отличимы от модели, которую они рассчитывают. Запишите формулы модели в одном имидже. Запишите формулы метода в другом (или оформите в виде функцииUser_function). Соедините соответствующим образом оба имиджа, и вы получите саморассчитывающуюся модель. Далее имиджем собственного метода вы можете пользоваться неоднократно и для других случаев.
Так метод Эйлера вообще система подключать не будет для решения нашей системы, рассмотренной в качестве примера выше, если соединить формулу модели и формулу метода.
f:=5-x
x:=x+~f*dt
Обозначений дифференциальных уравнений в этом случае не понадобилось.
Created with the Personal Edition of HelpNDoc: 5 Reasons Why a Help Authoring Tool is Better than Microsoft Word for Documentation